
Sinusoidal model
Encyclopedia
In statistics
, signal processing
, and time series analysis, a sinusoidal model to approximate a sequence Yi is:
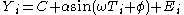
where C is constant defining a mean
level, α is an amplitude
for the sine wave
, ω is the frequency
, Ti is a time variable, φ is the phase
, and Ei is the error sequence in approximating the sequence Yi by the model. This sinusoidal model can be fit using nonlinear least squares; to obtain a good fit, nonlinear least squares routines may require good starting values for the constant, the amplitude, and the frequency.
Fitting a model with a single sinusoid is a special case of least-squares spectral analysis
.
of the data. If the data show a trend
, i.e., the assumption of constant location is violated, one can replace C with a linear or quadratic least squares
fit. That is, the model becomes
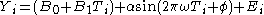
or
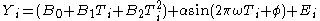
. A complex demodulation phase plot can be used to refine this initial estimate for the frequency.
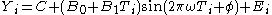
That is, one may replace α with a function of time. A linear fit is specified in the model above, but this can be replaced with a more elaborate function if needed.
, the fit should be subjected to graphical and quantitative techniques of model validation. For example, a run sequence plot to check for significant shifts in location, scale, start-up effects, and outliers. A lag plot can be used to verify the residuals
are independent. The outliers also appear in the lag plot, and a histogram
and normal probability plot
to check for skewness or other non-normality in the residuals.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, and time series analysis, a sinusoidal model to approximate a sequence Yi is:
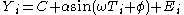
where C is constant defining a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
level, α is an amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
for the sine wave
Sine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
, ω is the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, Ti is a time variable, φ is the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, and Ei is the error sequence in approximating the sequence Yi by the model. This sinusoidal model can be fit using nonlinear least squares; to obtain a good fit, nonlinear least squares routines may require good starting values for the constant, the amplitude, and the frequency.
Fitting a model with a single sinusoid is a special case of least-squares spectral analysis
Least-squares spectral analysis
Least-squares spectral analysis is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis...
.
Good starting value for C
A good starting value for C can be obtained by calculating the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the data. If the data show a trend
Trend estimation
Trend estimation is a statistical technique to aid interpretation of data. When a series of measurements of a process are treated as a time series, trend estimation can be used to make and justify statements about tendencies in the data...
, i.e., the assumption of constant location is violated, one can replace C with a linear or quadratic least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
fit. That is, the model becomes
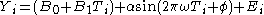
or
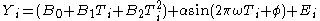
Good starting value for frequency
The starting value for the frequency can be obtained from the dominant frequency in a periodogramPeriodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
. A complex demodulation phase plot can be used to refine this initial estimate for the frequency.
Good starting values for amplitude
A complex demodulation amplitude plot can be used to find a good starting value for the amplitude. In addition, this plot can indicate whether or not the amplitude is constant over the entire range of the data or if it varies. If the plot is essentially flat, i.e., zero slope, then it is reasonable to assume a constant amplitude in the non-linear model. However, if the slope varies over the range of the plot, one may need to adjust the model to be: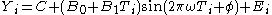
That is, one may replace α with a function of time. A linear fit is specified in the model above, but this can be replaced with a more elaborate function if needed.
Model validation
As with any statistical modelStatistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
, the fit should be subjected to graphical and quantitative techniques of model validation. For example, a run sequence plot to check for significant shifts in location, scale, start-up effects, and outliers. A lag plot can be used to verify the residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
are independent. The outliers also appear in the lag plot, and a histogram
Histogram
In statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
and normal probability plot
Normal probability plot
The normal probability plot is a graphical technique for normality testing: assessing whether or not a data set is approximately normally distributed....
to check for skewness or other non-normality in the residuals.

