
Least-squares spectral analysis
Encyclopedia
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum
, based on a least squares
fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems.
LSSA is also known as the Vaníček method after Petr Vaníček
, and as the Lomb method (or the Lomb periodogram) and the Lomb–Scargle method (or Lomb–Scargle periodogram), based on the contributions of Nicholas R. Lomb and, independently, Jeffrey D. Scargle. Closely related methods have been developed by Michael Korenberg and by Scott Chen and David Donoho
.
, and least-squares fitting of sinusoids have long been known. Most developments, however, are restricted to complete data sets of equally spaced samples. In 1963, J. F. M. Barning of Mathematisch Centrum, Amsterdam, handled unequally spaced data by similar techniques, including both a periodogram analysis equivalent to what is now referred to the Lomb method, and least-squares fitting of selected frequencies of sinusoids determined from such periodograms, connected by a procedure that is now known as matching pursuit
with post-backfitting or orthogonal matching pursuit.
Petr Vaníček
, a Canadian geodesist
of the University of New Brunswick
, also proposed the matching-pursuit approach, which he called "successive spectral analysis", but with equally spaced data, in 1969. He further developed this method, and analyzed the treatment of unequally spaced samples, in 1971.
The Vaníček method was then simplified in 1976 by Nicholas R. Lomb of the University of Sydney
, who pointed out its close connection to periodogram
analysis. The definition of a periodogram of unequally spaced data was subsequently further modified and analyzed by Jeffrey D. Scargle of NASA Ames Research Center
, who showed that with minor changes it could be made identical to Lomb's least-squares formula for fitting individual sinusoid frequencies.
Scargle states that his paper "does not introduce a new detection technique, but instead studies the reliability and efficiency of detection with the most commonly used technique, the periodogram, in the case where the observation times are unevenly spaced," and further points out in reference to least-squares fitting of sinusoids compared to periodogram analysis, that his paper "establishes, apparently for the first time, that (with the proposed modifications) these two methods are exactly equivalent."
Press summarizes the development this way:
Michael Korenberg of Queen's University in 1989 developed the "fast orthogonal search" method of more quickly finding a near-optimal decomposition of spectra or other problems, similar to the technique that later became known as orthogonal matching pursuit. In 1994, Scott Chen and David Donoho of Stanford University have developed the "basis pursuit" method using minimization of the L1 norm of coefficients to cast the problem as a linear programming
problem, for which efficient solutions are available.
, or least-squares fit. The frequencies are chosen using a method similar to Barning's, but going further in optimizing the choice of each successive new frequency by picking the frequency that minimizes the residual after least-squares fitting (equivalent to the fitting technique now known as matching pursuit
with pre-backfitting). The number of sinusoids must be less than or equal to the number of data samples (counting sines and cosines of the same frequency as separate sinusoids).
A data vector Φ is represented as a weighted sum of sinusoidal basis functions, tabulated in a matrix A by evaluating each function at the sample times, with weight vector x:

where the weight vector x is chosen to minimize the sum of squared errors in approximating Φ. The solution for x is closed-form, using standard linear regression
:
 .
.
Here the matrix A can be based on any set of functions that are mutually independent (not necessarily orthogonal) when evaluated at the sample times; for spectral analysis, the functions used are typically sines and cosines evenly distributed over the frequency range of interest. If too many frequencies are chosen in a too-narrow frequency range, the functions will not be sufficiently independent, the matrix will be badly conditioned, and the resulting spectrum will not be meaningful.
When the basis functions in A are orthogonal (that is, not correlated, meaning the columns have zero pair-wise dot product
s), the matrix ATA is a diagonal matrix; when the columns all have the same power (sum of squares of elements), then that matrix is an identity matrix
times a constant, so the inversion is trivial. The latter is the case when the sample times are equally spaced and the sinusoids are chosen to be sines and cosines equally spaced in pairs on the frequency interval 0 to a half cycle per sample (spaced by 1/N cycle per sample, omitting the sine phases at 0 and maximum frequency where they are identically zero). This particular case is known as the discrete Fourier transform
, slightly rewritten in terms of real data and coefficients.
 (DFT case for N equally spaced samples and frequencies, within a scalar factor)
(DFT case for N equally spaced samples and frequencies, within a scalar factor)
Lomb proposed using this simplification in general, except for pair-wise correlations between sine and cosine bases of the same frequency, since the correlations between pairs of sinusoids are often small, at least when they are not too closely spaced. This is essentially the traditional periodogram
formulation, but now adopted for use with unevenly spaced samples. The vector x is a good estimate of an underlying spectrum, but since correlations are ignored, Ax is no longer a good approximation to the signal, and the method is no longer a least-squares method – yet it has continued to be referred to as such.
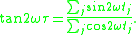
The periodogram at frequency ω is then estimated as:

which Scargle reports then has the same statistical distribution as the periodogram in the evenly-sampled case.
At any individual frequency ω, this method gives the same power as does a least-squares fit to sinusoids of that frequency, of the form
 .
.
, developed a method for choosing a sparse set of components from an over-complete set, such as sinusoidal components for spectral analysis, called fast orthogonal search (FOS). Mathematically, FOS uses a slightly modified Cholesky decomposition
in a mean-square error reduction (MSER) process, implemented as a sparse matrix
inversion. As with the other LSSA methods, FOS avoids the major shortcoming of discrete Fourier analysis, and can achieve highly accurate identifications of embedded periodicities and excels with unequally-spaced data; the fast orthogonal search method has also been applied to other problems such as nonlinear system identification.
problem, for which efficient solution methods are available.
This method is a fast technique (FFT-based) for doing weighted least-squares analysis on arbitrarily-spaced data with non-uniform standard errors. Source code that implements this technique is available.
Because data are often not sampled at uniformly spaced discrete times, this method "grids' the data by sparsely filling a time series array at the sample times. All intervening grid points receive zero statistical weight, equivalent to having infinite error bars at times between samples.
analyzed, without the need to manipulate the record or to invent otherwise non-existent data.
Magnitude
s in the LSSA spectrum
depict the contribution of a frequency or period to the variance
of the time series
. Generally, spectral magnitudes defined in the above manner enable the output's straightforward significance level regime. Alternatively, magnitudes in the Vanícek spectrum can also be expressed in dB
. Note that magnitudes in the Vaníček spectrum follow β-distribution.
Inverse
transformation of Vaníček's LSSA is possible, as is most easily seen by writing the forward transform as a matrix; the matrix inverse (when the matrix is not singular) or pseudo-inverse will then be an inverse transformation; the inverse will exactly match the original data if the chosen sinusoids are mutually independent at the sample points and their number is equal to the number of data points. No such inverse procedure is known for the periodogram method.
code. For each frequency in a desired set of frequencies, sine
and cosine functions are evaluated at the times corresponding to the data samples, and dot product
s of the data vector
with the sinusoid vectors are taken and appropriately normalized; following the method known as Lomb/Scargle periodogram, a time shift is calculated for each frequency to orthogonalize the sine and cosine components before the dot product, as described by Craymer; finally, a power
is computed from those two amplitude
components. This same process implements a discrete Fourier transform
when the data are uniformly spaced in time and the frequencies chosen correspond to integer numbers of cycles over the finite data record.
As Craymer explains, this method treats each sinusoidal component independently, or out of context, even though they may not be orthogonal on the data points, whereas Vaníček's original method does a full simultaneous least-squares fit by solving a matrix equation, partitioning the total data variance between the specified sinusoid frequencies. Such a matrix least-squares solution is natively available in MATLAB as the backslash
operator.
Craymer explains that the least-squares method, as opposed to the independent or periodogram version due to Lomb, can not fit more components (sines and cosines) than there are data samples, and further that:
Lomb's periodogram method, on the other hand, can use an arbitrarily high number of, or density of, frequency components, as in a standard periodogram
; that is, the frequency domain can be over-sampled by an arbitrary factor.
In Fourier analysis, such as the Fourier transform
or the discrete Fourier transform
, the sinusoids being fitted to the data are all mutually orthogonal, so there is no distinction between the simple out-of-context dot-product-based projection onto basis functions versus a least-squares fit; that is, no matrix inversion is required to least-squares partition the variance between orthogonal sinusoids of different frequencies. This method is usually preferred for its efficient fast Fourier transform
implementation, when complete data records with equally spaced samples are available.
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
, based on a least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems.
LSSA is also known as the Vaníček method after Petr Vaníček
Petr Vanícek
Petr Vaníček is a Czech Canadian geodesist and theoretical geophysicist who has made important breakthroughs in theory of spectral analysis and geoid computation. He initiated the establishing of the Canadian Geophysical Union in 1974, and served as the Union's president between 1986 and 1988...
, and as the Lomb method (or the Lomb periodogram) and the Lomb–Scargle method (or Lomb–Scargle periodogram), based on the contributions of Nicholas R. Lomb and, independently, Jeffrey D. Scargle. Closely related methods have been developed by Michael Korenberg and by Scott Chen and David Donoho
David Donoho
David Leigh Donoho, born on March 5, 1957 in Los Angeles, is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences...
.
Historical background
The close connections between Fourier analysis, the periodogramPeriodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
, and least-squares fitting of sinusoids have long been known. Most developments, however, are restricted to complete data sets of equally spaced samples. In 1963, J. F. M. Barning of Mathematisch Centrum, Amsterdam, handled unequally spaced data by similar techniques, including both a periodogram analysis equivalent to what is now referred to the Lomb method, and least-squares fitting of selected frequencies of sinusoids determined from such periodograms, connected by a procedure that is now known as matching pursuit
Matching pursuit
Matching pursuit is a type of numerical technique which involves finding the "best matching" projections of multidimensional data onto an over-complete dictionary D...
with post-backfitting or orthogonal matching pursuit.
Petr Vaníček
Petr Vanícek
Petr Vaníček is a Czech Canadian geodesist and theoretical geophysicist who has made important breakthroughs in theory of spectral analysis and geoid computation. He initiated the establishing of the Canadian Geophysical Union in 1974, and served as the Union's president between 1986 and 1988...
, a Canadian geodesist
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
of the University of New Brunswick
University of New Brunswick
The University of New Brunswick is a Canadian university located in the province of New Brunswick. UNB is the oldest English language university in Canada and among the first public universities in North America. The university has two main campuses: the original campus founded in 1785 in...
, also proposed the matching-pursuit approach, which he called "successive spectral analysis", but with equally spaced data, in 1969. He further developed this method, and analyzed the treatment of unequally spaced samples, in 1971.
The Vaníček method was then simplified in 1976 by Nicholas R. Lomb of the University of Sydney
University of Sydney
The University of Sydney is a public university located in Sydney, New South Wales. The main campus spreads across the suburbs of Camperdown and Darlington on the southwestern outskirts of the Sydney CBD. Founded in 1850, it is the oldest university in Australia and Oceania...
, who pointed out its close connection to periodogram
Periodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
analysis. The definition of a periodogram of unequally spaced data was subsequently further modified and analyzed by Jeffrey D. Scargle of NASA Ames Research Center
NASA Ames Research Center
The Ames Research Center , is one of the United States of America's National Aeronautics and Space Administration 10 major field centers.The centre is located in Moffett Field in California's Silicon Valley, near the high-tech companies, entrepreneurial ventures, universities, and other...
, who showed that with minor changes it could be made identical to Lomb's least-squares formula for fitting individual sinusoid frequencies.
Scargle states that his paper "does not introduce a new detection technique, but instead studies the reliability and efficiency of detection with the most commonly used technique, the periodogram, in the case where the observation times are unevenly spaced," and further points out in reference to least-squares fitting of sinusoids compared to periodogram analysis, that his paper "establishes, apparently for the first time, that (with the proposed modifications) these two methods are exactly equivalent."
Press summarizes the development this way:
Michael Korenberg of Queen's University in 1989 developed the "fast orthogonal search" method of more quickly finding a near-optimal decomposition of spectra or other problems, similar to the technique that later became known as orthogonal matching pursuit. In 1994, Scott Chen and David Donoho of Stanford University have developed the "basis pursuit" method using minimization of the L1 norm of coefficients to cast the problem as a linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem, for which efficient solutions are available.
The Vaníček method
In the Vaníček method, a discrete data set is approximated by a weighted sum of sinusoids of progressively determined frequencies, using a standard linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, or least-squares fit. The frequencies are chosen using a method similar to Barning's, but going further in optimizing the choice of each successive new frequency by picking the frequency that minimizes the residual after least-squares fitting (equivalent to the fitting technique now known as matching pursuit
Matching pursuit
Matching pursuit is a type of numerical technique which involves finding the "best matching" projections of multidimensional data onto an over-complete dictionary D...
with pre-backfitting). The number of sinusoids must be less than or equal to the number of data samples (counting sines and cosines of the same frequency as separate sinusoids).
A data vector Φ is represented as a weighted sum of sinusoidal basis functions, tabulated in a matrix A by evaluating each function at the sample times, with weight vector x:

where the weight vector x is chosen to minimize the sum of squared errors in approximating Φ. The solution for x is closed-form, using standard linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
:
 .
.Here the matrix A can be based on any set of functions that are mutually independent (not necessarily orthogonal) when evaluated at the sample times; for spectral analysis, the functions used are typically sines and cosines evenly distributed over the frequency range of interest. If too many frequencies are chosen in a too-narrow frequency range, the functions will not be sufficiently independent, the matrix will be badly conditioned, and the resulting spectrum will not be meaningful.
When the basis functions in A are orthogonal (that is, not correlated, meaning the columns have zero pair-wise dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s), the matrix ATA is a diagonal matrix; when the columns all have the same power (sum of squares of elements), then that matrix is an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
times a constant, so the inversion is trivial. The latter is the case when the sample times are equally spaced and the sinusoids are chosen to be sines and cosines equally spaced in pairs on the frequency interval 0 to a half cycle per sample (spaced by 1/N cycle per sample, omitting the sine phases at 0 and maximum frequency where they are identically zero). This particular case is known as the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, slightly rewritten in terms of real data and coefficients.
 (DFT case for N equally spaced samples and frequencies, within a scalar factor)
(DFT case for N equally spaced samples and frequencies, within a scalar factor)Lomb proposed using this simplification in general, except for pair-wise correlations between sine and cosine bases of the same frequency, since the correlations between pairs of sinusoids are often small, at least when they are not too closely spaced. This is essentially the traditional periodogram
Periodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
formulation, but now adopted for use with unevenly spaced samples. The vector x is a good estimate of an underlying spectrum, but since correlations are ignored, Ax is no longer a good approximation to the signal, and the method is no longer a least-squares method – yet it has continued to be referred to as such.
The Lomb–Scargle periodogram
Rather than just taking dot products of the data with sine and cosine waveforms directly, Scargle modified the standard periodogram formula to first find a time delay τ such that this pair of sinusoids would be mutually orthogonal at sample times tj, and also adjusted for the potentially unequal powers of these two basis functions, to obtain a better estimate of the power at a frequency, which made his modified periodogram method exactly equivalent to Lomb's least-squares method. The time delay τ is defined by the formula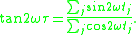
The periodogram at frequency ω is then estimated as:

which Scargle reports then has the same statistical distribution as the periodogram in the evenly-sampled case.
At any individual frequency ω, this method gives the same power as does a least-squares fit to sinusoids of that frequency, of the form
 .
.Korenberg's "fast orthogonal search" method
Michael Korenberg of Queens University in Kingston, OntarioKingston, Ontario
Kingston, Ontario is a Canadian city located in Eastern Ontario where the St. Lawrence River flows out of Lake Ontario. Originally a First Nations settlement called "Katarowki," , growing European exploration in the 17th Century made it an important trading post...
, developed a method for choosing a sparse set of components from an over-complete set, such as sinusoidal components for spectral analysis, called fast orthogonal search (FOS). Mathematically, FOS uses a slightly modified Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
in a mean-square error reduction (MSER) process, implemented as a sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
inversion. As with the other LSSA methods, FOS avoids the major shortcoming of discrete Fourier analysis, and can achieve highly accurate identifications of embedded periodicities and excels with unequally-spaced data; the fast orthogonal search method has also been applied to other problems such as nonlinear system identification.
Chen and Donoho's "basis pursuit" method
Chen and Donoho have developed a procedure called basis pursuit for fitting a sparse set of sinusoids or other functions from an over-complete set. The method defines an optimal solution as the one that minimizes the L1 norm of the coefficients, so that the problem can be cast as a linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem, for which efficient solution methods are available.
Palmer's Chi-squared method
Palmer has developed a method for finding the best-fit function to any chosen number of harmonics, allowing more freedom to find non-sinusoidal harmonic functions.This method is a fast technique (FFT-based) for doing weighted least-squares analysis on arbitrarily-spaced data with non-uniform standard errors. Source code that implements this technique is available.
Because data are often not sampled at uniformly spaced discrete times, this method "grids' the data by sparsely filling a time series array at the sample times. All intervening grid points receive zero statistical weight, equivalent to having infinite error bars at times between samples.
Applications
The most useful feature of the LSSA method is enabling incomplete records to be spectrallyFrequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
analyzed, without the need to manipulate the record or to invent otherwise non-existent data.
Magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
s in the LSSA spectrum
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
depict the contribution of a frequency or period to the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
. Generally, spectral magnitudes defined in the above manner enable the output's straightforward significance level regime. Alternatively, magnitudes in the Vanícek spectrum can also be expressed in dB
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
. Note that magnitudes in the Vaníček spectrum follow β-distribution.
Inverse
Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....
transformation of Vaníček's LSSA is possible, as is most easily seen by writing the forward transform as a matrix; the matrix inverse (when the matrix is not singular) or pseudo-inverse will then be an inverse transformation; the inverse will exactly match the original data if the chosen sinusoids are mutually independent at the sample points and their number is equal to the number of data points. No such inverse procedure is known for the periodogram method.
Implementation
The LSSA can be implemented in less than a page of MATLABMATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code. For each frequency in a desired set of frequencies, sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine functions are evaluated at the times corresponding to the data samples, and dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s of the data vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
with the sinusoid vectors are taken and appropriately normalized; following the method known as Lomb/Scargle periodogram, a time shift is calculated for each frequency to orthogonalize the sine and cosine components before the dot product, as described by Craymer; finally, a power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
is computed from those two amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
components. This same process implements a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
when the data are uniformly spaced in time and the frequencies chosen correspond to integer numbers of cycles over the finite data record.
As Craymer explains, this method treats each sinusoidal component independently, or out of context, even though they may not be orthogonal on the data points, whereas Vaníček's original method does a full simultaneous least-squares fit by solving a matrix equation, partitioning the total data variance between the specified sinusoid frequencies. Such a matrix least-squares solution is natively available in MATLAB as the backslash
Backslash
The backslash is a typographical mark used mainly in computing. It was first introduced to computers in 1960 by Bob Bemer. Sometimes called a reverse solidus or a slosh, it is the mirror image of the common slash....
operator.
Craymer explains that the least-squares method, as opposed to the independent or periodogram version due to Lomb, can not fit more components (sines and cosines) than there are data samples, and further that:
Lomb's periodogram method, on the other hand, can use an arbitrarily high number of, or density of, frequency components, as in a standard periodogram
Periodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
; that is, the frequency domain can be over-sampled by an arbitrary factor.
In Fourier analysis, such as the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, the sinusoids being fitted to the data are all mutually orthogonal, so there is no distinction between the simple out-of-context dot-product-based projection onto basis functions versus a least-squares fit; that is, no matrix inversion is required to least-squares partition the variance between orthogonal sinusoids of different frequencies. This method is usually preferred for its efficient fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
implementation, when complete data records with equally spaced samples are available.
See also
- Orthogonal functionsOrthogonal functionsIn mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...
- Sinusoidal modelSinusoidal modelIn statistics, signal processing, and time series analysis, a sinusoidal model to approximate a sequence Yi is:Y_i = C + \alpha\sin + E_i...
- Spectral densitySpectral densityIn statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
- Spectral density estimationSpectral density estimationIn statistical signal processing, the goal of spectral density estimation is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal...
External links
- [ftp://ftp.geod.nrcan.gc.ca/pub/GSD/craymer/software/lssa/ LSSA software freeware download] (via ftp), FORTRAN, Vaníček's method, from the Natural Resources CanadaNatural Resources CanadaThe Department of Natural Resources , operating under the FIP applied title Natural Resources Canada , is the ministry of the government of Canada responsible for natural resources, energy, minerals and metals, forests, earth sciences, mapping and remote sensing...
. - Least-Squares Spectral Analysis Research Website at the University of New Brunswick, containing literature, source code, and sample dataset

