Cantor space
Encyclopedia
In mathematics
, a Cantor space, named for Georg Cantor
, is a topological
abstraction of the classical Cantor set
: a topological space
is a Cantor space if it is homeomorphic to the Cantor set
. In set theory
, the topological space 2ω is called "the" Cantor space. Note that, commonly, 2ω is referred to simply as the Cantor set, while the term Cantor space is reserved for the more general construction of DS for a finite set D and a set S which might be finite, countable or possibly uncountable.
of the discrete 2-point space {0, 1}. This is usually written as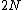
or 2ω (where 2 denotes the 2-element set {0,1} with the discrete topology). A point in 2ω is an infinite binary sequence, that is a sequence which assumes only the values 0 or 1. Given such a sequence a1, a2, a3,..., one can map it to the real number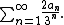
This mapping gives a homeomorphism from 2ω onto the Cantor set
, demonstrating that 2ω is indeed a Cantor space.
Cantor spaces occur in abundance in real analysis
. For example they exist as subspaces in every perfect, complete
metric space
. (To see this, note that in such a space, any non-empty perfect set contains two disjoint non-empty perfect subsets of arbitrarily small diameter, and so one can imitate the construction
of the usual Cantor set
.) Also, every uncountable,
separable, completely metrizable space contains
Cantor spaces as subspaces. This includes most of the common type of spaces in real analysis.
's theorem:
The topological property of having a base consisting of clopen sets is sometimes known as "zero-dimensionality". Brouwer's theorem can be restated as:
This theorem is also equivalent (via Stone's representation theorem for Boolean algebras
) to the fact that any two countable atomless Boolean algebras are isomorphic.
Cantor spaces have the following properties:
Let C(X) denote the space of all real-valued, bounded continuous functions on a topological space X. Let K denote a compact metric space, and Δ denote the Cantor set. Then the Cantor set has the following property:
In general, this isometry is not unique, and thus is not properly a universal property
in the categorical sense.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Cantor space, named for Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, is a topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
abstraction of the classical Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
: a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a Cantor space if it is homeomorphic to the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
. In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the topological space 2ω is called "the" Cantor space. Note that, commonly, 2ω is referred to simply as the Cantor set, while the term Cantor space is reserved for the more general construction of DS for a finite set D and a set S which might be finite, countable or possibly uncountable.
Examples
The Cantor set itself is of course a Cantor space. But the canonical example of a Cantor space is the countably infinite topological productProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of the discrete 2-point space {0, 1}. This is usually written as
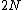or 2ω (where 2 denotes the 2-element set {0,1} with the discrete topology). A point in 2ω is an infinite binary sequence, that is a sequence which assumes only the values 0 or 1. Given such a sequence a1, a2, a3,..., one can map it to the real number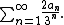This mapping gives a homeomorphism from 2ω onto the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, demonstrating that 2ω is indeed a Cantor space.
Cantor spaces occur in abundance in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. For example they exist as subspaces in every perfect, complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. (To see this, note that in such a space, any non-empty perfect set contains two disjoint non-empty perfect subsets of arbitrarily small diameter, and so one can imitate the construction
of the usual Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
.) Also, every uncountable,
separable, completely metrizable space contains
Cantor spaces as subspaces. This includes most of the common type of spaces in real analysis.
Characterization
A topological characterization of Cantor spaces is given by BrouwerLuitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
's theorem:
- Any two non-empty compact Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s without isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s and having countable baseBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
s consisting of clopen setClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
s are homeomorphic to each other.
The topological property of having a base consisting of clopen sets is sometimes known as "zero-dimensionality". Brouwer's theorem can be restated as:
- A topological space is a Cantor space if and only if it is non-empty, perfectPerfect spaceIn mathematics, in the field of topology, perfect spaces are spaces that have no isolated points. In such spaces, every point can be approximated arbitrarily well by other points - given any point and any topological neighborhood of the point, there is another point within the neighborhood.The...
, compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, totally disconnected, and metrizable.
This theorem is also equivalent (via Stone's representation theorem for Boolean algebras
Stone's representation theorem for Boolean algebras
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
) to the fact that any two countable atomless Boolean algebras are isomorphic.
Properties
As can be expected from Brouwer's theorem, Cantor spaces appear in several forms. But many properties of Cantor spaces can be established using 2ω, because its construction as a product makes it amenable to analysis.Cantor spaces have the following properties:
- The cardinality of any Cantor space is
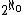, that is, the cardinality of the continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. - The product of two (or even any finite or countable number of) Cantor spaces is a Cantor space. Along with the Cantor functionCantor functionIn mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
; this fact can be used to construct space-filling curveSpace-filling curveIn mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
s. - A Hausdorff topological space is compact metrizable if and only if it is a continuous image of a Cantor space.
Let C(X) denote the space of all real-valued, bounded continuous functions on a topological space X. Let K denote a compact metric space, and Δ denote the Cantor set. Then the Cantor set has the following property:
- C(K) is isometricIsometricThe term isometric comes from the Greek for "having equal measurement".isometric may mean:* Isometric projection , a method for the visual representation of three-dimensional objects in two dimensions; a form of orthographic projection, or more specifically, an axonometric projection.* Isometry and...
to a closed subspace of C(Δ).
In general, this isometry is not unique, and thus is not properly a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in the categorical sense.