Space-filling curve
Encyclopedia
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a space-filling curve is a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
whose range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
contains the entire 2-dimensional unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
(or more generally an N-dimensional hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
). Because Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
(1858–1932) was the first to discover one, space-filling curves in the 2-dimensional plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
are commonly called Peano curves.
Definition
Intuitively, a continuous curve in 2 or 3 (or higher) dimensions can be thought of as the path of a continuously moving point. To eliminate the inherent vagueness of this notion JordanCamille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
in 1887 introduced the following rigorous definition, which has since been adopted as the precise description of the notion of a continuous curve:
- A curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
(with endpoints) is a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
whose domain is the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1].
In the most general form, the range of such a function may lie in an arbitrary topological space, but in the most common cases, the range will lie in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
such as the 2-dimensional plane (a planar curve) or the 3-dimensional space (space curve).
Sometimes, the curve is identified with the range or image of the function (the set of all possible values of the function), instead of the function itself. It is also possible to define curves without endpoints to be a continuous function on the real line (or on the open unit interval (0, 1)).
History
In 1890, Peano discovered a densely self-intersecting curve that passes through every point of the unit square. His purpose was to construct a continuous mapping from the unit intervalUnit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
onto the unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
. Peano was motivated by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's earlier counterintuitive result that the infinite number of points in a unit interval is the same cardinality as the infinite number of points in any finite-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, such as the unit square. The problem Peano solved was whether such a mapping could be continuous; i.e., a curve that fills a space.
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
differentiable (that is, have piecewise continuous derivatives), and such curves cannot fill up the entire unit square. Therefore, Peano's space-filling curve was found to be highly counterintuitive.
From Peano's example, it was easy to deduce continuous curves whose ranges contained the n-dimensional hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
(for any positive integer n). It was also easy to extend Peano's example to continuous curves without endpoints which filled the entire n-dimensional Euclidean space (where n is 2, 3, or any other positive integer).
Most well-known space-filling curves are constructed iteratively as the limit of a sequence of piecewise linear continuous curves, each one more closely approximating the space-filling limit.
Peano's ground-breaking paper contained no illustrations of his construction, which is defined in terms of ternary expansions and a mirroring operator. But the graphical construction was perfectly clear to him—he made an ornamental tiling showing a picture of the curve in his home in Turin. Peano's paper also ends by mentioning (without proof) that the technique can be extended to other odd bases besides base 3. His choice to avoid any appeal to graphical visualization was no doubt motivated by a desire for a well-founded, completely rigorous proof owing nothing to pictures. At that time (the beginning of the foundation of general topology), graphical arguments were still included in proofs, yet were becoming a hindrance to understanding often counter-intuitive results.
A year later, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
published in the same journal a variation of Peano's construction. Hilbert's paper was the first to include a picture helping to visualize the construction technique, essentially the same as illustrated here. The analytic form of the Hilbert curve, however, is more complicated than Peano's.
Outline of the construction of a space-filling curve
Let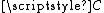
denote the Cantor spaceCantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
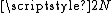.We start with a continuous function
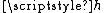from the Cantor space 
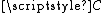onto the entire unit interval 
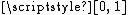. (The restriction of the Cantor functionCantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
to the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is an example of such a function.) From it, we get a continuous function
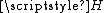from the topological product 
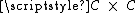onto the entire unit square 
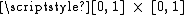by setting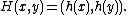
Since the Cantor set is homeomorphic to the product
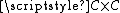, there is a continuous bijection 
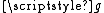from the Cantor set onto 
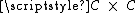. The composition 
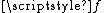of 
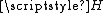and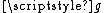 
is a continuous function mapping the Cantor set onto the entire unit square. (Alternatively, we could use the theorem that every compact metric space is a continuous image of the Cantor set to get the function 
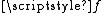.)Finally, one can extend
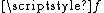to a continuous function 
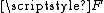whose domain is the entire unit interval 
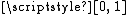. This can be done either by using the Tietze extension theorem on each of the components of 
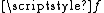, or by simply extending 
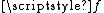"linearly" (that is, on each of the deleted open interval 
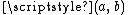in the construction of the Cantor set, we define the extension part of 
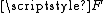on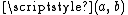 
to be the line segment within the unit square joining the values 
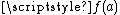and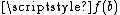 
).Properties
A space-filling curve must be everywhere self-intersecting in the technical sense that the curve is not injective. If a curve is not injective, then one can find two subcurves of the curve, each obtained by considering the images of two disjoint segments from the curve's domain (the unit line segment). The two subcurves intersect if the intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the two images is non-empty. One might be tempted to think that the meaning of curves intersecting is that they necessarily cross each other, like the intersection point of two non-parallel lines, from one side to the other. However, two curves (or two subcurves of one curve) may contact one another without crossing, as, for example, a line tangent to a circle does.
A non-self-intersecting continuous curve cannot fill the unit square because that will make the curve a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
from the unit interval onto the unit square (any continuous bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
onto a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is a homeomorphism). But a unit-square has no cut-point
Cut-point
In topology, a cut-point is a point of a connected space such that its removal causes the resulting space to be disconnected. For example every point of a line is a cut-point, while no point of a circle is a cut-point...
, and so cannot be homeomorphic to the unit interval, in which all points except the endpoints are cut-points.
For the classic Peano and Hilbert space-filling curves, where two subcurves intersect (in the technical sense), there is self-contact without self-crossing. A space-filling curve can be (everywhere) self-crossing if its approximation curves are self-crossing. A space-filling curve's approximations can be self-avoiding, as the figures above illustrate. In 3 dimensions, self-avoiding approximation curves can even contain knot
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
s. Approximation curves remain within a bounded portion of n-dimensional space, but their lengths increase without bound.
Space-filling curves are special cases of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
constructions. No differentiable space-filling curve can exist. Roughly speaking, differentiability puts a bound on how fast the curve can turn.
Proof that a square and its side contain the same number of points
The highly counterintuitiveCounterintuitive
The word "counterintuitive" literally means counter to intuition, and so it essentially means that something does not seem right or correct.A counterintuitive proposition is one that does not seem likely to be true when assessed using intuition or gut feelings...
result that the cardinality of a unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
is the same as the cardinality of any finite-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, such as the unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
, was first obtained by Cantor in 1878, but it can be more intuitively proved using space-filling curves.
Intuitively, consider that the main difficulty resided in showing that a function of the unit interval can fill a square, a cube, or a hypercube, and this task was successfully accomplished by Peano. Indeed, being self-intersecting, his curves even manage to "overfill" the square. In other words, although Peano curves are not injective (because they overfill the space), they are surjective (because they fill it). This is true whether their self-intersection is self-crossing, or merely self-contacting.
Formally, a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between a set A and a set B is needed to prove that A and B have the same cardinality. Since space-filling curves "overfill" the space, they are not bijections. Thus, their existence is not a direct proof that a square (or cube or hypercube) contains as many points as its side. However, the right inverse of a space-filling curve is an injection, and can be used to obtain such a proof via the Cantor–Bernstein–Schroeder theorem
Cantor–Bernstein–Schroeder theorem
In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
, which asserts the existence of a bijection between A and B given that injections
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
exist both from A into B and from B into A.
For instance, consider a space-filling curve that maps a unit interval A = [0, 1] onto a unit square B = [0, 1] × [0, 1]. This is a surjection from A into B, but one can define a right inverse for it which will be an injection from B into A. And x goes to (x,0) is an injection from A into B. Using the Cantor–Bernstein–Schroeder theorem, we get a bijection between A and B, the existence of which implies that A and B have the same cardinality.
One advantage of this proof is that, because an explicit definition of the right inverse is easily given, it does not require the use of the axiom of choice. For example, in the Hilbert curve each point in the square is the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of from one to four points in the line segment. When one of the coordinates is a rational number with a power of two in the denominator, that coordinate can be approached either from below or above giving two (not necessarily distinct) values for the preimage. Similarly, when both are such, then there are four (not necessarily distinct). Since the number of possible preimages for each point is finite (indeed less than or equal to four), one can just choose the smallest of them systematically, making the axiom of choice unnecessary.
Similarly, finite-dimensional space-filling curves can be used to prove, in general, that any finite-dimensional space contains the same number of points as any line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
or line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
.
The Hahn–Mazurkiewicz theorem
The Hahn–Mazurkiewicz theorem is the following characterization of spaces that are the continuous image of curves:- A non-empty Hausdorff topological space is a continuous image of the unit interval if and only if it is a compact, connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, locally connected second-countable spaceSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
.
Spaces that are the continuous image of a unit interval are sometimes called Peano spaces.
In many formulations of the Hahn–Mazurkiewicz theorem, second-countable is replaced by metrizable. These two formulations are equivalent. In one direction a compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is a normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
and, by the Urysohn
Pavel Samuilovich Urysohn
Pavel Samuilovich Urysohn, Pavel Uryson was a Jewish mathematician who is best known for his contributions in the theory of dimension, and for developing Urysohn's Metrization Theorem and Urysohn's Lemma, both of which are fundamental results in topology...
metrization theorem
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
, second-countable then implies metrizable. Conversely a compact metric space is second-countable.
Kleinian groups
There are many natural examples of space-filling, or rather sphere-filling, curves in the theory of doubly degenerate Kleinian groups. For example,showed that the circle at infinity of the universal cover of a fiber of a mapping torus of a pseudo-Anosov map
Pseudo-Anosov map
In mathematics, specifically in topology, a pseudo-Anosov map is a type of a diffeomorphism or homeomorphism of a surface. It is a generalization of a linear Anosov diffeomorphism of the torus...
is a sphere-filling curve. (Here the sphere is the sphere at infinity of hyperbolic 3-space.)
See also
- Dragon curveDragon curveA dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
- Gosper curveGosper curveThe Gosper curve, named after Bill Gosper, also known as the flowsnake , is a space-filling curve. It is a fractal object similar in its construction to the dragon curve and the Hilbert curve....
- Moore curveMoore curveA Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.Because the Moore...
- Sierpiński curveSierpinski curveSierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit n \rightarrow \infty completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling...
- Space-filling treeSpace-filling treeSpace-filling trees are geometric constructions that are analogous to space-filling curves, but have a branching, tree-like structure and are rooted. A space-filling tree is defined by an incremental process that results in a tree for which every point in the space has a finite-length path that...
- Hilbert R-treeHilbert R-treeHilbert R-tree, an R-tree variant, is an index for multidimensional objects like lines, regions, 3-D objects, or high dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects....
- Hilbert curveHilbert curveA Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling curves discovered by Giuseppe Peano in 1890....
- Bx-treeBx-tree Moving Object IndexIn computer science, the Bx tree is a query and update efficient B+ tree-based index structure for moving objects.-Index structure:The base structure of the Bx-tree is a B+ tree in which the internal nodes serve as a directory, each containing a pointer to its right sibling...
- Z-order (Morton-order)Z-order (curve)In mathematical analysis and computer science, Z-order, Morton order, or Morton code is a space-filling curve which maps multidimensional data to one dimension while preserving locality of the data points. It was introduced in 1966 by G. M. Morton...
- List of fractals by Hausdorff dimension
- Osgood curveOsgood curveIn mathematics, an Osgood curve is a Jordan curve of positive area. The first example was found by .Examples of Osgood curves can be produced by slightly modifying one of the constructions of space-filling curves with image the unit square to make it an embedding, though the cost is that it no...
External links
- Multidimensional Space-Filling Curves
- Proof of the existence of a bijection at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
Java applets:
- Peano Plane Filling Curves at cut-the-knot
- Hilbert's and Moore's Plane Filling Curves at cut-the-knot
- All Peano Plane Filling Curves at cut-the-knot