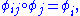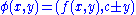Pseudo-Anosov map
Encyclopedia
In mathematics
, specifically in topology
, a pseudo-Anosov map is a type of a diffeomorphism
or homeomorphism
of a surface
. It is a generalization of a linear Anosov diffeomorphism
of the torus
. Its definition relies on the notion of a measured foliation invented by William Thurston
, who also coined the term "pseudo-Anosov diffeomorphism" when he proved his classification of diffeomorphisms of a surface.
and a measure in the transverse direction. In some neighborhood of a regular point of F, there is a "flow box" φ: U → R2 which sends the leaves of F to the horizontal lines in R2. If two such neighborhoods Ui and Uj overlap then there is a transition function φij defined on φj(Uj), with the standard property
which must have the form
for some constant c. This assures that along a simple curve, the variation in y-coordinate, measured locally in every chart, is a geometric quantity (i.e. independent of the chart) and permits the definition of a total variation along a simple closed curve on S. A finite number of singularities of F of the type of "p-pronged saddle", p≥3, are allowed. At such a singular point, the differentiable structure of the surface is modified to make the point into a conical point with the total angle πp. The notion of a diffeomorphism of S is redefined with respect to this modified differentiable structure. With some technical modifications, these definitions extend to the case of a surface with boundary.
of a closed surface S is called pseudo-Anosov if there exists a transverse pair of measured foliations on S, Fs (stable) and Fu (unstable), and a real number λ > 1 such that the foliations are preserved by f and their transverse measures are multiplied by 1/λ and λ.
T(S) of a surface S such that the action induced on T(S) by any diffeomorphism f of S extends to a homeomorphism of the Thurston compactification. The dynamics of this homeomorphism is the simplest when f is a pseudo-Anosov map: in this case, there are two fixed points on the Thurston boundary, one attracting and one repelling, and the homeomorphism behaves similarly to a hyperbolic automorphism of the Poincaré half-plane. A "generic" diffeomorphism of a surface of genus at least two is isotopic to a pseudo-Anosov diffeomorphism.
s (on the algebraic side). This leads to an analogue of Thurston classification for the case of automorphisms of free groups, developed by Bestvina
and Handel.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a pseudo-Anosov map is a type of a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
or homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
. It is a generalization of a linear Anosov diffeomorphism
Anosov diffeomorphism
In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
of the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. Its definition relies on the notion of a measured foliation invented by William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
, who also coined the term "pseudo-Anosov diffeomorphism" when he proved his classification of diffeomorphisms of a surface.
Definition of a measured foliation
A measured foliation F on a closed surface S is a geometric structure on S which consists of a singular foliationFoliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
and a measure in the transverse direction. In some neighborhood of a regular point of F, there is a "flow box" φ: U → R2 which sends the leaves of F to the horizontal lines in R2. If two such neighborhoods Ui and Uj overlap then there is a transition function φij defined on φj(Uj), with the standard property
which must have the form
for some constant c. This assures that along a simple curve, the variation in y-coordinate, measured locally in every chart, is a geometric quantity (i.e. independent of the chart) and permits the definition of a total variation along a simple closed curve on S. A finite number of singularities of F of the type of "p-pronged saddle", p≥3, are allowed. At such a singular point, the differentiable structure of the surface is modified to make the point into a conical point with the total angle πp. The notion of a diffeomorphism of S is redefined with respect to this modified differentiable structure. With some technical modifications, these definitions extend to the case of a surface with boundary.
Definition of a pseudo-Anosov map
A homeomorphism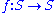
of a closed surface S is called pseudo-Anosov if there exists a transverse pair of measured foliations on S, Fs (stable) and Fu (unstable), and a real number λ > 1 such that the foliations are preserved by f and their transverse measures are multiplied by 1/λ and λ.
Significance
Thurston constructed a compactification of the Teichmüller spaceTeichmüller space
In mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
T(S) of a surface S such that the action induced on T(S) by any diffeomorphism f of S extends to a homeomorphism of the Thurston compactification. The dynamics of this homeomorphism is the simplest when f is a pseudo-Anosov map: in this case, there are two fixed points on the Thurston boundary, one attracting and one repelling, and the homeomorphism behaves similarly to a hyperbolic automorphism of the Poincaré half-plane. A "generic" diffeomorphism of a surface of genus at least two is isotopic to a pseudo-Anosov diffeomorphism.
Generalization
Using the theory of train tracks, the notion of a pseudo-Anosov map has been extended to self-maps of graphs (on the topological side) and outer automorphisms of free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s (on the algebraic side). This leads to an analogue of Thurston classification for the case of automorphisms of free groups, developed by Bestvina
Mladen Bestvina
Mladen Bestvina is a Croatian American mathematician working in the area of geometric group theory. He is a Distinguished Professor in the Department of Mathematics at the University of Utah.-Biographical info:...
and Handel.