Second-countable space
Encyclopedia
In topology
, a second-countable space, also called a completely separable space, is a topological space
satisfying the second axiom of countability
. A space is said to be second-countable if its topology has a countable base
. More explicitly, this means that a topological space
is second countable if there exists some countable collection 
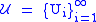of open subsets of 
such that any open subset of 
can be written as a union of elements of some subfamily of 
. Like other countability axioms, the property of being second-countable restricts the number of open set
s that a space can have.
Most "well-behaved
" spaces in mathematics
are second-countable. For example, Euclidean space
(Rn) with its usual topology is second-countable. Although the usual base of open balls is not countable, one can restrict to the set of all open balls with rational
radii and whose centers have rational coordinates. This restricted set is countable and still forms a base.
. Recall that a space is first-countable if each point has a countable local base. Given a base for a topology and a point x, the set of all basis sets containing x forms a local base at x. Thus, if one has a countable base for a topology then one clearly has a countable local base at every point.
Second-countability implies certain other topological properties. Specifically, every second-countable space is separable (has a countable dense subset) and Lindelöf
(every open cover has a countable subcover). The reverse implications do not hold. For example, the lower limit topology
on the real line is first-countable, separable, and Lindelöf, but not second-countable. For metric space
s, however, the properties of being second-countable, separable, and Lindelöf are all equivalent. Therefore, the lower limit topology on the real line is not metrizable.
In second-countable spaces—as in metric spaces—compactness
, sequential compactness, and countable compactness are all equivalent properties.
Urysohn
's metrization theorem
states that every second-countable, regular space
is metrizable. It follows that every such space is completely normal as well as paracompact. Second-countability is therefore a rather restrictive property on a topological space, requiring only a separation axiom to imply metrizability.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a second-countable space, also called a completely separable space, is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
satisfying the second axiom of countability
Axiom of countability
In mathematics, an axiom of countability is a property of certain mathematical objects that requires the existence of a countable set with certain properties, while without it such sets might not exist....
. A space is said to be second-countable if its topology has a countable base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
. More explicitly, this means that a topological space
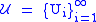is second countable if there exists some countable collection of open subsets of such that any open subset of can be written as a union of elements of some subfamily of . Like other countability axioms, the property of being second-countable restricts the number of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s that a space can have.
Most "well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
" spaces in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
are second-countable. For example, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(Rn) with its usual topology is second-countable. Although the usual base of open balls is not countable, one can restrict to the set of all open balls with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
radii and whose centers have rational coordinates. This restricted set is countable and still forms a base.
Properties
Second-countability is a stronger notion than first-countabilityFirst-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
. Recall that a space is first-countable if each point has a countable local base. Given a base for a topology and a point x, the set of all basis sets containing x forms a local base at x. Thus, if one has a countable base for a topology then one clearly has a countable local base at every point.
Second-countability implies certain other topological properties. Specifically, every second-countable space is separable (has a countable dense subset) and Lindelöf
Lindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
(every open cover has a countable subcover). The reverse implications do not hold. For example, the lower limit topology
Lower limit topology
In mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
on the real line is first-countable, separable, and Lindelöf, but not second-countable. For metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, however, the properties of being second-countable, separable, and Lindelöf are all equivalent. Therefore, the lower limit topology on the real line is not metrizable.
In second-countable spaces—as in metric spaces—compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, sequential compactness, and countable compactness are all equivalent properties.
Urysohn
Pavel Samuilovich Urysohn
Pavel Samuilovich Urysohn, Pavel Uryson was a Jewish mathematician who is best known for his contributions in the theory of dimension, and for developing Urysohn's Metrization Theorem and Urysohn's Lemma, both of which are fundamental results in topology...
's metrization theorem
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
states that every second-countable, regular space
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
is metrizable. It follows that every such space is completely normal as well as paracompact. Second-countability is therefore a rather restrictive property on a topological space, requiring only a separation axiom to imply metrizability.
Other properties
- A continuous, open imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a second-countable space is second-countable. - Every subspace of a second-countable space is second-countable.
- QuotientsQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of second-countable spaces need not be second-countable; however, open quotients always are. - Any countable product of a second-countable space is second-countable, although uncountable products need not be.
- The topology of a second-countable space has cardinality less than or equal to c (the cardinality of the continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
). - Any base for a second-countable space has a countable subfamily which is still a base.
- Every collection of disjoint open sets in a second-countable space is countable.
Examples
- Consider the disjoint countable union
. Define an equivalence relation and a quotient topology by identifying the left ends of the intervals - that is, identify 0 ~ 2 ~ 4 ~ ... ~ 2k and so on. X is second countable, as a countable union of second countable spaces. However, X/~ is not first countable at the coset of the identified points and hence also not second countable. - Note that the above space is not homeomorphic to the same set of equivalence classes endowed with the obvious metric: i.e. regular Euclidean distance for two points in the same interval, and the sum of the distances to the left hand point for points not in the same interval. It is a separable metric space (consider the set of rational points), and hence is second-countable.