Hilbert curve
Encyclopedia
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
space-filling curve
Space-filling curve
In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
first described by the German mathematician David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in 1891, as a variant of the space-filling curves discovered by Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
in 1890.
Because it is space-filling, its Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
is
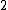(precisely, its image is the unit square, whose dimension is 2 in any definition of dimension; its graph is a compact set homeomorphic to the closed unit interval, with Hausdorff dimension 2).
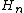is the 
th approximation to the limiting curve. The Euclidean lengthEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
of
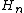is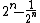 
, i.e., it grows exponentially with 
, while at the same time always being bounded by a square with a finite area.Applications and mapping algorithms
Both the true Hilbert curve and its discrete approximations are useful because they give a mapping between 1D and 2D space that fairly well preserves locality. If (x,y) is the coordinates of a point within the unit square, and d is the distance along the curve when it reaches that point, then points that have nearby d values will also have nearby (x,y) values. The converse can't always be true. There will sometimes be points where the (x,y) coordinates are close but their d values are far apart. This is inevitable when mapping from a 2D space to a 1D space. But the Hilbert curve does a good job of keeping those d values close together much of the time. So the mappings in both direction do a fairly good job of maintaining locality.Because of this locality property, the Hilbert curve is widely used in computer science. For example, the range of IP addresses
IP address
An Internet Protocol address is a numerical label assigned to each device participating in a computer network that uses the Internet Protocol for communication. An IP address serves two principal functions: host or network interface identification and location addressing...
used by computers can be mapped into a picture using the Hilbert curve. Code to generate the image would map from 2D to 1D to find the color of each pixel, and the Hilbert curve is sometimes used because it keeps nearby IP addresses close to each other in the picture. A grayscale photograph can be converted to a dithered black and white image using thresholding, with the leftover amount from each pixel added to the next pixel along the Hilbert curve. Code to do this would map from 1D to 2D, and the Hilbert curve is sometimes used because it does not create the distracting patterns that would be visible to the eye if the order were simply left to right across each row of pixels. Hilbert curves in higher dimensions are a generalization of Gray codes
Gray code
The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....
, and are sometimes used for similar purposes, for similar reasons. For multidimensional databases, Hilbert order has been proposed to be used instead of Z order
Z-order (curve)
In mathematical analysis and computer science, Z-order, Morton order, or Morton code is a space-filling curve which maps multidimensional data to one dimension while preserving locality of the data points. It was introduced in 1966 by G. M. Morton...
because it has better locality-preserving behavior.
Given the variety of applications, it is useful to have algorithms to map in both directions. In many languages, these are better if implemented with iteration rather than recursion. The following C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
code performs the mappings in both directions, using iteration and bit operations rather than recursion. It assumes a square divided into n by n cells, for n a power of 2, with integer coordinates, with (0,0) in the lower left corner, (n-1,n-1) in the upper right corner, and a distance d that starts at 0 in the lower left corner and goes to
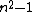in the lower-right corner.//convert (x,y) to d
int xy2d (int n, int x, int y) {
int rx, ry, s, d=0;
for (s=n/2; s>0; s/=2) {
rx = (x & s) > 0;
ry = (y & s) > 0;
d += s * s * ((3 * rx) ^ ry);
rot(s, &x, &y, rx, ry);
}
return d;
}
//convert d to (x,y)
void d2xy(int n, int d, int *x, int *y) {
int rx, ry, s, t=d;
*x = *y = 0;
for (s=1; s
ry = 1 & (t ^ rx);
rot(s, x, y, rx, ry);
*x += s * rx;
*y += s * ry;
t /= 4;
}
}
//rotate/flip a quadrant appropriately
void rot(int n, int *x, int *y, int rx, int ry) {
int t;
if (ry
0) {
if (rx
1) {*x = n-1 - *x;
*y = n-1 - *y;
}
t = *x;
*x = *y;
*y = t;
}
}
These use the C conventions: the & symbol is a bitwise AND, the ^ symbol is a bitwise XOR, the += operator adds on to a variable, and the /= operator divides a variable. The handling of booleans in C means that in xy2d, the variable rx is set to 0 or 1 to match bit s of x, and similarly for ry.
The xy2d function works top down, starting with the most significant bits of x and y, and building up the most significant bits of d first. The d2xy function works in the opposite order, starting with the least significant bits of d, and building up x and y starting with the least significant bits. Both functions use the rotation function to rotate and flip the (x,y) coordinate system appropriately.
The two mapping algorithms work in similar ways. The entire square is viewed as composed of 4 regions, arranged 2 by 2. Each region is composed of 4 smaller regions, and so on, for a number of levels. At level s, each region is s by s cells. There is a single FOR loop that iterates through levels. On each iteration, an amount is added to d or to x and y, determined by which of the 4 regions it is in at the current level. The current region out of the 4 is (rx,ry), where rx and ry are each 0 or 1. So it consumes 2 input bits, (either 2 from d or 1 each from x and y), and generates two output bits. It also calls the rotation function so that (x,y) will be appropriate for the next level, on the next iteration. For xy2d, it starts at the top level of the entire square, and works its way down to the lowest level of individual cells. For d2xy, it starts at the bottom with cells, and works up to include the entire square.
Representation as Lindenmayer system
The Hilbert Curve can be expressed by a rewrite systemRewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
(L-system
L-system
An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
).
- Alphabet : A, B
- Constants : f, l, r
- Axiom : A
- Production rules:
- A → l B fr A f A rf B l
- B → r A fl B f B lf A r
Here, f means "draw forward", l means "turn left 90°", and r means "turn right 90°" (see turtle graphics
Turtle graphics
Turtle graphics is a term in computer graphics for a method of programming vector graphics using a relative cursor upon a Cartesian plane...
).
Arthur Butz
Arthur Butz
Arthur R. Butz is a Holocaust denier and associate professor of electrical engineering at Northwestern University. He achieved tenure in 1974 and currently teaches classes in control system theory and digital signal processing.-Education:...
provided an algorithm for calculating the Hilbert curve in multidimensions.
Graphics Gems II discusses Hilbert Curve coherency, and provides implementation.
Implementation
In the Python programming language:from turtle import left, right, forward
size = 4
def hilbert(level, angle):
if level
0:
return
right(angle)
hilbert(level - 1, -angle)
forward(size)
left(angle)
hilbert(level - 1, angle)
forward(size)
hilbert(level - 1, angle)
left(angle)
forward(size)
hilbert(level - 1, -angle)
right(angle)
hilbert(5, 90)
See also
- Hilbert R-treeHilbert R-treeHilbert R-tree, an R-tree variant, is an index for multidimensional objects like lines, regions, 3-D objects, or high dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects....
- Sierpiński curveSierpinski curveSierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit n \rightarrow \infty completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling...
- Moore curveMoore curveA Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.Because the Moore...
- Space-filling curves
- List of fractals by Hausdorff dimension
External links
Hilbert R-tree
Hilbert R-tree, an R-tree variant, is an index for multidimensional objects like lines, regions, 3-D objects, or high dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects....
Sierpinski curve
Sierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit n \rightarrow \infty completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling...
Moore curve
A Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.Because the Moore...