
List of fractals by Hausdorff dimension
Encyclopedia
According to Falconer, one of the essential features of a fractal
is that its Hausdorff dimension
strictly exceeds its topological dimension.
Presented here is a list of fractals ordered by increasing Hausdorff dimension, with the purpose of visualizing what it means for a fractal to have a low or a high dimension.
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
is that its Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
strictly exceeds its topological dimension.
Presented here is a list of fractals ordered by increasing Hausdorff dimension, with the purpose of visualizing what it means for a fractal to have a low or a high dimension.
Deterministic fractals
| Hausdorff dimension (exact value) |
Hausdorff dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
| Calculated | 0.538 | Feigenbaum attractor Logistic map The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations... |
The Feigenbaum attractor (see between arrows) is the set of points generated by successive iterations of the logistic function Logistic function A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P... for the critical parameter value 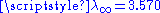 , where the period doubling is infinite. Notice that this dimension is the same for any differentiable and unimodal function. , where the period doubling is infinite. Notice that this dimension is the same for any differentiable and unimodal function. |
|
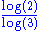 |
0.6309 | Cantor set Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... |
 |
Built by removing the central third at each iteration. Nowhere dense and not a countable set Countable set In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor... . |
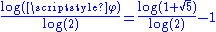 |
0.6942 | Asymmetric Cantor set Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... |
Note that the dimension is not 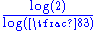 , as would be expected from the generalized Cantor set with γ=1/4, which has the same length at each stage. , as would be expected from the generalized Cantor set with γ=1/4, which has the same length at each stage.Built by removing the second quarter at each iteration. Nowhere dense and not a countable set Countable set In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor... . 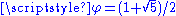 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
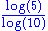 |
0.69897 | Real number Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... s with even digits |
Similar to a Cantor set Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... . |
|
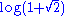 |
0.88137 | Spectrum of Fibonacci Hamiltonian | The study the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant. | |
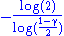 |
0| Generalized Cantor set |
|
Built by removing at the |
 th iteration the central interval of length th iteration the central interval of length 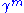 from each remaining segment. At from each remaining segment. At 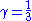 one obtains the usual Cantor set one obtains the usual Cantor setCantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... . Varying 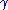 between 0 and 1 yields any fractal dimension between 0 and 1 yields any fractal dimension 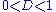 . . |
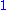 |
1 | Smith–Volterra–Cantor set |  |
Built by removing a central interval of length 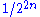 of each remaining interval at the nth iteration. Nowhere dense but has a Lebesgue measure of each remaining interval at the nth iteration. Nowhere dense but has a Lebesgue measureLebesgue measure In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called... of ½. |
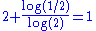 |
1 | Takagi or Blancmange curve | Defined on the unit interval by 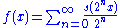 , where , where 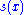 is the sawtooth function. Special case of the Takahi-Landsberg curve: is the sawtooth function. Special case of the Takahi-Landsberg curve: 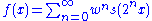 with with 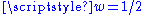 . The Hausdorff dimension equals . The Hausdorff dimension equals 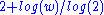 for for  in in  . (Hunt cited by Mandelbrot ). . (Hunt cited by Mandelbrot ). |
|
| Calculated | 1.0812 | Julia set Julia set In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function... z² + 1/4 |
Julia set for c = 1/4. | |
| 1.0933 | Boundary of the Rauzy fractal Rauzy fractal thumb|300px|Rauzy fractalIn mathematics, the Rauzy fractal is a fractal set associated to the Tribonacci substitutionIt has been studied in 1981 by Gérard Rauzy, with the idea of generalizing the dynamic properties of the Fibonacci morphism.... |
Fractal representation introduced by G.Rauzy of the dynamics associated to the Tribonacci morphism: 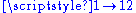 , , 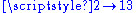 and and 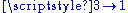 . .  is one of the conjugated roots of is one of the conjugated roots of 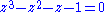 . . |
||
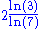 |
1.12915 | contour of the Gosper island |  |
Term used by Mandelbrot (1977). The Gosper island is the limit of the Gosper curve Gosper curve The Gosper curve, named after Bill Gosper, also known as the flowsnake , is a space-filling curve. It is a fractal object similar in its construction to the dragon curve and the Hilbert curve.... . |
| Measured (box counting) | 1.2 | Dendrite Julia set Julia set In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function... |
Julia set for parameters: Real = 0 and Imaginary = 1. | |
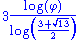 |
1.2083 | Fibonacci word fractal 60° Fibonacci word thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits... |
Build from the Fibonacci word Fibonacci word thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits... . See also the standard Fibonacci word fractal. 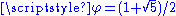 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
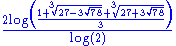 |
1.2108 | Boundary of the tame twindragon | One of the six 2-rep-tile Rep-tile In the geometry of tessellations, a shape that can be dissected into smaller copies of the same shape is called a reptile or rep-tile. The shape is labelled as rep-n if the dissection uses n copies... s in the plane (can be tiled by two copies of itself, of equal size). |
|
| 1.26 | Hénon map | The canonical Hénon map (with parameters a = 1.4 and b = 0.3) has Hausdorff dimension 1.261 ± 0.003. Different parameters yield different dimension values. | ||
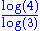 |
1.2619 | Koch curve | 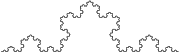 |
3 von Koch curves form the Koch snowflake or the anti-snowflake. |
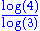 |
1.2619 | boundary of Terdragon curve Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
L-system: same as dragon curve with angle = 30°. The Fudgeflake is based on 3 initial segments placed in a triangle. | |
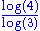 |
1.2619 | 2D Cantor dust | Cantor set in 2 dimensions. | |
| Calculated | 1.2683 | Julia set Julia set In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function... z2 − 1 |
Julia set for c = −1. | |
| 1.3057 | Apollonian gasket Apollonian gasket In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:... |
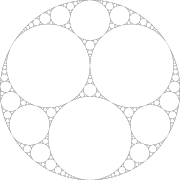 |
Starting with 3 tangent circles, repeatedly packing new circles into the complementary interstices. Also the limit set generated by reflections in 4 mutually tangent circles. See | |
| Calculated (Box counting) | 1.328 | 5 circles inversion fractal | The limit set generated by iterated inversions with respect to 5 mutually tangent circles (in red). Also an Apollonian packing. See | |
| Calculated | 1.3934 | Douady rabbit Douady rabbit The Douady rabbit, named for the French mathematician Adrien Douady, is any of various particular filled Julia sets associated with the c near the center period 3 buds of Mandelbrot set for complex quadratic map.-Forms of the complex quadratic map:... |
Julia set for c = −0,123 + 0.745i. | |
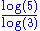 |
1.4649 | Vicsek fractal Vicsek fractal In mathematics the Vicsek fractal, also known as Vicsek snowflake or box fractal, is a fractal arising from a construction similar to that of the Sierpinski carpet. It has applications including as compact antennas, particularly in cellular phones.... |
 |
Built by exchanging iteratively each square by a cross of 5 squares. |
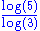 |
1.4649 | Quadratic von Koch curve (type 1) | 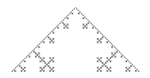 |
One can recognize the pattern of the Vicsek fractal (above). |
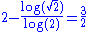 (conjectured exact) (conjectured exact) |
1.5000 | a Weierstrass function Weierstrass function In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere... : 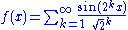 |
The Hausdorff dimension of the Weierstrass function 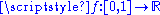 defined by defined by 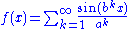 with with 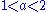 and and  has upper bound has upper bound 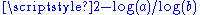 . It is believed to be the exact value. The same result can be established when, instead of the sine function, we use other periodic functions, like cosine. . It is believed to be the exact value. The same result can be established when, instead of the sine function, we use other periodic functions, like cosine. |
|
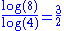 |
1.5000 | Quadratic von Koch curve (type 2) |  |
Also called "Minkowski sausage". |
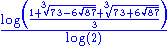 |
1.5236 | Boundary of the Dragon curve Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
cf. Chang & Zhang. | |
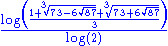 |
1.5236 | Boundary of the twindragon curve Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
Can be built with two dragon curves. One of the six 2-rep-tile Rep-tile In the geometry of tessellations, a shape that can be dissected into smaller copies of the same shape is called a reptile or rep-tile. The shape is labelled as rep-n if the dissection uses n copies... s in the plane (can be tiled by two copies of itself, of equal size). |
|
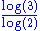 |
1.5849 | 3-branches tree | Each branch carries 3 branches (here 90° and 60°). The fractal dimension of the entire tree is the fractal dimension of the terminal branches. NB: the 2-branches tree has a fractal dimension of only 1. | |
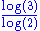 |
1.5849 | Sierpinski triangle Sierpinski triangle The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral... |
Also the triangle of Pascal modulo 2. | |
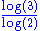 |
1.5849 | Sierpiński arrowhead curve Sierpinski arrowhead curve The Sierpiński arrowhead curve is a fractal curve similar in appearance and identical in limit to the Sierpiński triangle.-Representation as Lindenmayer system:The Sierpiński arrowhead curve can be expressed by a rewrite system .-Literature:... |
Same limit as the triangle (above) but built with a one-dimensional curve. | |
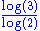 |
1.5849 | Boundary of the T-Square T-Square (fractal) In mathematics, the T-square is a two-dimensional fractal. As all two-dimensional fractals, it has a boundary of infinite length bounding a finite area... fractal |
.png) |
|
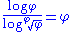 |
1.61803 | a golden dragon Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
Built from two similarities of ratios  and and 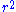 , with , with 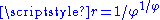 . Its dimension equals . Its dimension equals  because because 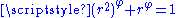 . With . With 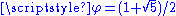 (Golden number (Golden numberGolden number Golden number may mean:* Golden number , a number assigned to a calendar year denoting its place in a Metonic cycle* Golden ratio, an irrational mathematical constant with special properties in arts and mathematics... ). |
|
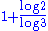 |
1.6309 | Pascal triangle modulo 3 | For a triangle modulo k, if k is prime, the fractal dimension is 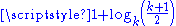 (cf. Stephen Wolfram (cf. Stephen WolframStephen Wolfram Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :... ). |
|
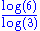 |
1.6309 | Sierpinski Hexagon | Built in the manner of the Sierpinski carpet Sierpinski carpet The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional... , on an hexagonal grid, with 6 similitudes of ratio 1/3. Notice the presence of the Koch snowflake Koch snowflake The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described... at all scales. |
|
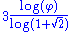 |
1.6379 | Fibonacci word fractal Fibonacci word thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits... |
Fractal based on the Fibonacci word Fibonacci word thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits... (or Rabbit sequence) Sloane A005614. Illustration : Fractal curve after 23 steps (F23 = 28657 segments). 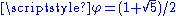 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
Solution of 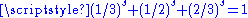 |
1.6402 | Attractor of IFS Iterated function system In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar.... with 3 similarities Similarity (geometry) Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other... of ratios 1/3, 1/2 and 2/3 |
Generalization : Providing the open set condition holds, the attractor of an iterated function system Iterated function system In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar.... consisting of  similarities of ratios similarities of ratios 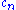 , has Hausdorff dimension , has Hausdorff dimension  , solution of the equation : , solution of the equation : 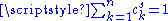 . . |
|
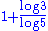 |
1.6826 | Pascal triangle modulo 5 | For a triangle modulo k, if k is prime, the fractal dimension is 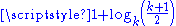 (cf. Stephen Wolfram (cf. Stephen WolframStephen Wolfram Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :... ). |
|
| Measured (box-counting) | 1.7 | Ikeda map attractor | For parameters a=1, b=0.9, k=0.4 and p=6 in the Ikeda map 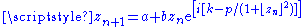 . It derives from a model of the plane-wave interactivity field in an optical ring laser. Different parameters yield different values. . It derives from a model of the plane-wave interactivity field in an optical ring laser. Different parameters yield different values. |
|
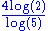 |
1.7227 | Pinwheel fractal Pinwheel tiling Pinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway.They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations.... |
Built with Conway's Pinwheel tile. | |
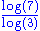 |
1.7712 | Hexaflake Hexaflake A hexaflake is a fractal constructed by iteratively exchanging each hexagon by a flake of seven hexagons; it is a special case of the n-flake. As such, a hexaflake would have 7n-1 hexagons in its nth iteration. Its boundary is the von Koch flake, and contains an infinite number of Koch snowflakes... |
 |
Built by exchanging iteratively each hexagon by a flake of 7 hexagons. Its boundary is the von Koch flake and contains an infinity of Koch snowflakes (black or white). |
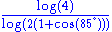 |
1.7848 | Von Koch curve 85° |  |
Generalizing the von Koch curve with an angle a chosen between 0 and 90°. The fractal dimension is then 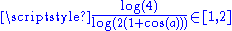 . . |
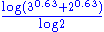 |
1.8272 | A self-affine Affine transformation In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property... fractal set |
Build iteratively from a 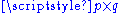 array on a square, with array on a square, with 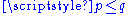 . Its Hausdorff dimension equals . Its Hausdorff dimension equals 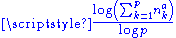 with with  and and 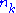 is the number of elements in the is the number of elements in the 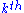 column. The box-counting dimension yields a different formula, therefore, a different value. Unlike self-similar sets, the Hausdorff dimension of self-affine sets depends on the position of the iterated elements and there is no formula, so far, for the general case. column. The box-counting dimension yields a different formula, therefore, a different value. Unlike self-similar sets, the Hausdorff dimension of self-affine sets depends on the position of the iterated elements and there is no formula, so far, for the general case. |
|
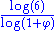 |
1.8617 | Pentaflake | Built by exchanging iteratively each pentagon by a flake of 6 pentagons.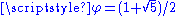 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
solution of 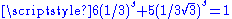 |
1.8687 | Monkeys tree | This curve appeared in Benoit Mandelbrot Benoît Mandelbrot Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child... 's "Fractal geometry of Nature" (1983). It is based on 6 similarities of ratio 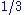 and 5 similarities of ratio and 5 similarities of ratio 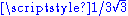 . . |
|
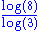 |
1.8928 | Sierpinski carpet Sierpinski carpet The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional... |
Each face of the Menger sponge is a Sierpinski carpet, as is the bottom surface of the 3D quadratic Koch surface (type 1). | |
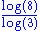 |
1.8928 | 3D Cantor dust | Cantor set in 3 dimensions. | |
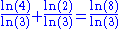 |
Cartesian product of the von Koch curve and the Cantor set Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... |
Generalization : Let FxG be the cartesian product of two fractals sets F and G. Then 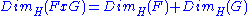 . See also the 2D Cantor dust and the Cantor cube. . See also the 2D Cantor dust and the Cantor cube. |
||
| Estimated | 1.9340 | Boundary of the Lévy C curve Lévy C curve In mathematics, the Lévy C curve is a self-similar fractal that was first described and whose differentiability properties were analysed by Ernesto Cesàro in 1906 and G... |
Estimated by Duvall and Keesling (1999). The curve itself has a fractal dimension of 2. | |
| 1.974 | Penrose tiling Penrose tiling A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original... |
See Ramachandrarao, Sinha & Sanyal. | ||
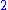 |
2 | Boundary of the Mandelbrot set Mandelbrot set The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape... |
The boundary and the set itself have the same dimension. | |
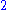 |
2 | Julia set Julia set In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function... |
For determined values of c (including c belonging to the boundary Misiurewicz point A Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic... of the Mandelbrot set), the Julia set has a dimension of 2. |
|
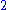 |
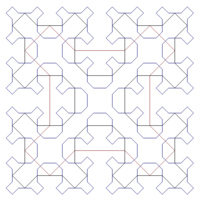
2 | Sierpiński curve Sierpinski curve Sierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit n \rightarrow \infty completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling... |
 |
Every Peano curve filling the plane has a Hausdorff dimension of 2. |
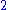 |
2 | Hilbert curve Hilbert curve A Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling curves discovered by Giuseppe Peano in 1890.... |
 |
|
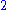 |
2 | Peano curve | And a family of curves built in a similar way, such as the Wunderlich curves. | |
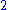 |
2 | Moore curve Moore curve A Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.Because the Moore... |
Can be extended in 3 dimensions. | |
| 2 | Lebesgue curve or z-order curve Z-order (curve) In mathematical analysis and computer science, Z-order, Morton order, or Morton code is a space-filling curve which maps multidimensional data to one dimension while preserving locality of the data points. It was introduced in 1966 by G. M. Morton... |
Unlike the previous ones this space-filling curve is differentiable almost everywhere. Another type can be defined in 2D. Like the Hilbert Curve it can be extended in 3D. | ||
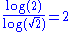 |
2 | Dragon curve Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
And its boundary has a fractal dimension of 1.5236270862. | |
| 2 | Terdragon curve Dragon curve A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:... |
L-system: F → F + F – F, angle = 120°. | ||
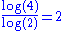 |
2 | Gosper curve Gosper curve The Gosper curve, named after Bill Gosper, also known as the flowsnake , is a space-filling curve. It is a fractal object similar in its construction to the dragon curve and the Hilbert curve.... |
 |
Its boundary is the Gosper island. |
Solution of 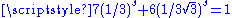 |
2 | Curve filling the Koch snowflake Koch snowflake The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described... |
Proposed by Mandelbrot in 1982, it fills the Koch snowflake Koch snowflake The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described... . It is based on 7 similarities of ratio 1/3 and 6 similarities of ratio 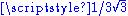 . . |
|
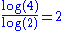 |
2 | Sierpiński tetrahedron Sierpinski triangle The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral... |
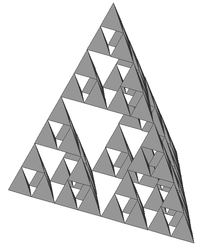 |
Each tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... is replaced by 4 tetrahedra. |
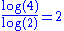 |
2 | H-fractal | Also the Mandelbrot tree which has a similar pattern. | |
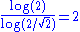 |
Pythagoras tree (fractal) |  |
Every square generates two squares with a reduction ratio of sqrt(2)/2. | |
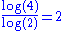 |
2 | 2D Greek cross fractal | Each segment is replaced by a cross formed by 4 segments. | |
| Measured | 2.01 ±0.01 | Rössler attractor Rössler attractor The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor... |
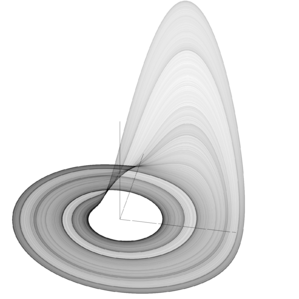 |
The fractal dimension of the Rössler attractor is slightly above 2. For a=0.1, b=0.1 and c=14 it has been estimated between 2.01 and 2.02. |
| Measured | 2.06 ±0.01 | Lorenz attractor Lorenz attractor The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape... |
For parameters v=40, =16 and b=4 . See McGuinness (1983) =16 and b=4 . See McGuinness (1983) |
|
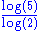 |
2.3219 | Fractal pyramid | Each pyramid is replaced by 5 pyramids, twice smaller. Must not be confused with the Sierpinski tetrahedron, since it is based on a square pyramid. | |
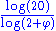 |
2.3296 | Dodecahedron fractal | Each dodecahedron is replaced by 20 dodecahedra.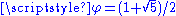 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
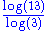 |
2.3347 | 3D quadratic Koch surface (type 1) | .png) |
Extension in 3D of the quadratic Koch curve (type 1). The illustration shows the second iteration. |
| 2.4739 | Apollonian sphere packing Apollonian sphere packing Apollonian sphere packing is the three dimensional equivalent of the Apollonian gasket. The principle of construction is very similar: with any four spheres that are cotangent to each other, it is then possible to construct two more spheres that are cotangent to four of them.The fractal dimension... |
The interstice left by the Apollonian spheres. Apollonian gasket in 3D. Dimension calculated by M. Borkovec, W. De Paris, and R. Peikert. | ||
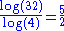 |
2.50 | 3D quadratic Koch surface (type 2) | Extension in 3D of the quadratic Koch curve (type 2). The illustration shows the second iteration. | |
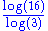 |
2.5237 | Cantor tesseract | no image available | Cantor set in 4 dimensions. Generalization: in a space of dimension n, the Cantor set has a Hausdorff dimension of  . . |
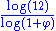 |
2.5819 | Icosahedron fractal | Each icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... is replaced by 12 icosahedra. 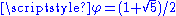 (golden ratio (golden ratioGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... ). |
|
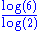 |
2.5849 | 3D Greek cross fractal | Each segment is replaced by a cross formed by 6 segments. | |
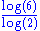 |
2.5849 | Octahedron fractal | Each octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... is replaced by 6 octahedra. |
|
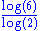 |
2.5849 | von Koch surface | 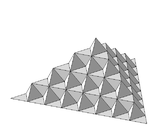 |
Each equilateral triangular face is cut into 4 equal triangles. Using the central triangle as the base, form a tetrahedron. Replace the triangular base with the tetrahedral "tent". |
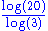 |
2.7268 | Menger sponge Menger sponge In mathematics, the Menger sponge is a fractal curve. It is a universal curve, in that it has topological dimension one, and any other curve is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge... |
And its surface has a fractal dimension of 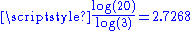 , which is the same as that by volume. , which is the same as that by volume. |
|
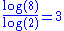 |
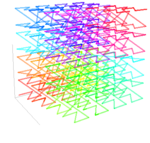
3 | 3D Hilbert curve Hilbert curve A Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling curves discovered by Giuseppe Peano in 1890.... |
 |
A Hilbert curve extended to 3 dimensions. |
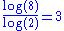 |
3 | 3D Lebesgue curve Z-order (curve) In mathematical analysis and computer science, Z-order, Morton order, or Morton code is a space-filling curve which maps multidimensional data to one dimension while preserving locality of the data points. It was introduced in 1966 by G. M. Morton... |
 |
A Lebesgue curve extended to 3 dimensions. |
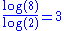 |
3 | 3D Moore curve Moore curve A Moore curve is a continuous fractal space-filling curve which is a variant of the Hilbert curve. Precisely, it is the loop version of the Hilbert curve, and it may be thought as the union of four copies of the Hilbert curves combined in such a way to make the endpoints coincide.Because the Moore... |
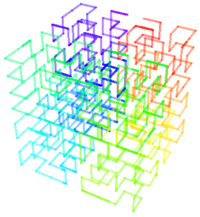 |
A Moore curve extended to 3 dimensions. |
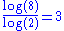 |
3 | 3D H-fractal | A H-fractal extended to 3 dimensions. | |
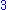 |
Mandelbulb Mandelbulb The Mandelbulb is a three-dimensional analogue of the Mandelbrot set, constructed by Daniel White and Paul Nylander using spherical coordinates.... |
Extension of the Mandelbrot set (power 8) in 3 dimensions |
Random and natural fractals
| Hausdorf dimension (exact value) |
Hausdorf dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
| 1/2 | 0.5 | Zeros of a Wiener process Wiener process In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown... |
 |
The zeros of a Wiener process (Brownian motion) are a nowhere dense set Nowhere dense set In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it... of Lebesgue measure Lebesgue measure In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called... 0 with a fractal structure. |
Solution of 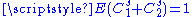 where where 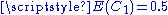 and and 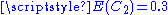 |
0.7499 | a random Cantor set Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.... with 50% - 30% |
Generalization : At each iteration, the length of the left interval is defined with a random variable 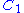 , a variable percentage of the length of the original interval. Same for the right interval, with a random variable , a variable percentage of the length of the original interval. Same for the right interval, with a random variable 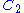 . Its Hausdorff Dimension . Its Hausdorff Dimension  satisfies : satisfies : 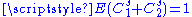 . ( . (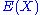 is the expected value is the expected valueExpected value In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on... of 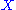 ). ). |
|
Solution of 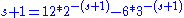 |
1.144... | von Koch curve with random interval | The length of the middle interval is a random variable with uniform distribution on the interval (0,1/3). | |
| Measured | 1.25 | Coastline of Great Britain How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2... |
Fractal dimension of the west coast of Great Britain, as measured by Lewis Fry Richardson Lewis Fry Richardson Lewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them... and cited by Benoît Mandelbrot Benoît Mandelbrot Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child... . |
|
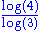 |
1.2619 | von Koch curve with random orientation | One introduces here an element of randomness which does not affect the dimension, by choosing, at each iteration, to place the equilateral triangle above or below the curve. | |
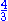 |
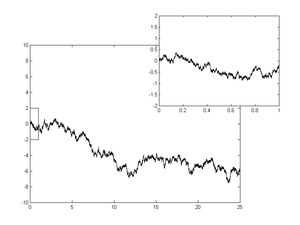
1.333 | Boundary of Brownian motion | (cf. Mandelbrot, Lawler, Schramm Oded Schramm Oded Schramm was an Israeli-American mathematician known for the invention of the Schramm–Loewner evolution and for working at the intersection of conformal field theory and probability theory.-Biography:... , Werner Wendelin Werner Wendelin Werner is a German-born French mathematician working in the area of self-avoiding random walks, Schramm-Loewner evolution, and related theories in probability theory and mathematical physics. In 2006, at the 25th International Congress of Mathematicians in Madrid, Spain he received the... ). |
|
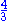 |
1.333 | 2D polymer | Similar to the brownian motion in 2D with non self-intersection. | |
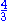 |
1.333 | Percolation front in 2D, Corrosion front in 2D | Fractal dimension of the percolation-by-invasion front (accessible perimeter), at the percolation threshold Percolation threshold Percolation threshold is a mathematical term related to percolation theory, which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist while above it, there exists a giant component of the order of system size... (59.3%). It’s also the fractal dimension of a stopped corrosion front. |
|
| 1.40 | Clusters of clusters 2D Diffusion-limited aggregation Diffusion-limited aggregation is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by Witten and Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means... |
When limited by diffusion, clusters combine progressively to a unique cluster of dimension 1.4. | ||
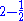 |
1.5 | Graph of a regular Brownian function (Wiener process Wiener process In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown... ) |
 |
Graph of a function f such that, for any two positive reals x and x+h, the difference of their images 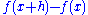 has the centered gaussian distribution with variance = h. Generalization : The fractional Brownian motion of index has the centered gaussian distribution with variance = h. Generalization : The fractional Brownian motion of index  follows the same definition but with a variance follows the same definition but with a variance 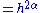 , in that case its Hausdorff dimension = , in that case its Hausdorff dimension = . . |
| Measured | 1.52 | Coastline of Norway Fjord Geologically, a fjord is a long, narrow inlet with steep sides or cliffs, created in a valley carved by glacial activity.-Formation:A fjord is formed when a glacier cuts a U-shaped valley by abrasion of the surrounding bedrock. Glacial melting is accompanied by rebound of Earth's crust as the ice... |
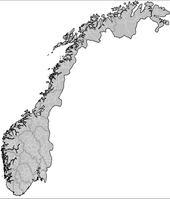 |
See J. Feder. |
| Measured | 1.55 | Random walk with no self-intersection | Self-avoiding random walk in a square lattice, with a « go-back » routine for avoiding dead ends. | |
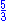 |
1.66 | 3D polymer | Similar to the brownian motion in a cubic lattice, but without self-intersection. | |
| 1.70 | 2D DLA Cluster Diffusion-limited aggregation Diffusion-limited aggregation is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by Witten and Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means... |
In 2 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 1.70. | ||
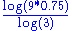 |
1.7381 | Fractal percolation with 75% probability | The fractal percolation model is constructed by the progressive replacement of each square by a 3x3 grid in which is placed a random collection of sub-squares, each sub-square being retained with probability p. The "almost sure" Hausdorff dimension equals 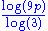 . . |
|
| 7/4 | 1.75 | 2D percolation cluster hull | The hull or boundary of a percolation cluster. Can also be generated by a hull-generating walk, or by Schramm-Loewner Evolution. | |
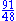 |
1.8958 | 2D percolation cluster | In a square lattice, under the site percolation threshold Percolation threshold Percolation threshold is a mathematical term related to percolation theory, which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist while above it, there exists a giant component of the order of system size... (59.3%) the percolation-by-invasion cluster has a fractal dimension of 91/48. Beyond that threshold, the cluster is infinite and 91/48 becomes the fractal dimension of the « clearings ». |
|
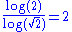 |
2 | Brownian motion Brownian motion Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications... |
Or random walk. The Hausdorff dimensions equals 2 in 2D, in 3D and in all greater dimensions (K.Falconer "The geometry of fractal sets"). | |
| Measured | Around 2 | Distribution of galaxy cluster Galaxy cluster A galaxy cluster is a compact cluster of galaxies. Basic difference between a galaxy group and a galaxy cluster is that there are many more galaxies in a cluster than in a group. Also, galaxies in a cluster are more compact and have higher velocity dispersion. One of the key features of cluster is... s |
 |
From the 2005 results of the Sloan Digital Sky Survey. |
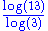 |
2.33 | Cauliflower Cauliflower Cauliflower is one of several vegetables in the species Brassica oleracea, in the family Brassicaceae. It is an annual plant that reproduces by seed... |
Every branch carries around 13 branches 3 times smaller. | |
| 2.5 | Balls of crumpled paper | When crumpling sheets of different sizes but made of the same type of paper and with the same aspect ratio (for example, different sizes in the ISO 216 ISO 216 ISO 216 specifies international standard paper sizes used in most countries in the world today. It defines the "A" and "B" series of paper sizes, including A4, the most commonly available size... A series), then the diameter of the balls so obtained elevated to a non-integer exponent between 2 and 3 will be approximately proportional to the area of the sheets from which the balls have been made. Creases will form at all size scales (see Universality (dynamical systems) Universality (dynamical systems) In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together... ). |
||
| 2.50 | 3D DLA Cluster Diffusion-limited aggregation Diffusion-limited aggregation is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by Witten and Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means... |
In 3 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 2.50. | ||
| 2.50 | Lichtenberg figure Lichtenberg figure Lichtenberg figures are branching electric discharges that sometimes appear on the surface or the interior of insulating materials. They are named after the German physicist Georg Christoph Lichtenberg, who originally discovered and studied them... |
 |
Their appearance and growth appear to be related to the process of diffusion-limited aggregation or DLA. | |
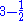 |
2.5 | regular Brownian Brownian motion Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications... surface |
A function  , gives the height of a point , gives the height of a point 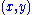 such that, for two given positive increments such that, for two given positive increments 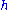 and and 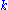 , then , then 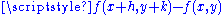 has a centered Gaussian distribution with variance = has a centered Gaussian distribution with variance = 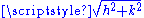 . Generalization : The fractional Brownian surface of index . Generalization : The fractional Brownian surface of index  follows the same definition but with a variance = follows the same definition but with a variance = 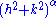 , in that case its Hausdorff dimension = , in that case its Hausdorff dimension =  . . |
|
| Measured | 2.52 | 3D percolation Percolation theory In mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:... cluster |
In a cubic lattice, at the site percolation threshold Percolation threshold Percolation threshold is a mathematical term related to percolation theory, which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist while above it, there exists a giant component of the order of system size... (31.1%), the 3D percolation-by-invasion cluster has a fractal dimension of around 2.52. Beyond that threshold, the cluster is infinite. |
|
| Measured | 2.66 | Broccoli Broccoli Broccoli is a plant in the cabbage family, whose large flower head is used as a vegetable.-General:The word broccoli, from the Italian plural of , refers to "the flowering top of a cabbage".... |
||
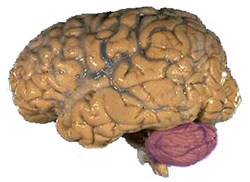
| 2.79 | Surface of human brain Cerebral cortex The cerebral cortex is a sheet of neural tissue that is outermost to the cerebrum of the mammalian brain. It plays a key role in memory, attention, perceptual awareness, thought, language, and consciousness. It is constituted of up to six horizontal layers, each of which has a different... |
 |
||
| 2.97 | Lung surface | The alveoli of a lung form a fractal surface close to 3. | ||
| Calculated | 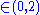 |
Multiplicative cascade Multiplicative Cascade In mathematics, a multiplicative cascade is a fractal/multifractal distribution of points produced via an iterative and multiplicative random process.Model I :Model II :Model III :... |
This is an example of a multifractal distribution. However by choosing its parameters in a particular way we can force the distribution to become a monofractal. |
See also
- Fractal dimensionFractal dimensionIn fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
- Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
- Scale invarianceScale invarianceIn physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
Further reading
- Benoît Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman & Co; ISBN 0-7167-1186-9 (September 1982).
- Heinz-Otto Peitgen, The Science of Fractal Images, Dietmar Saupe (editor), Springer Verlag, ISBN 0-387-96608-0 (August 1988)
- Michael F. Barnsley, Fractals Everywhere, Morgan Kaufmann; ISBN 0-12-079061-0
- Bernard Sapoval, « Universalités et fractales », collection Champs, Flammarion. ISBN 2080814664 (2001).

