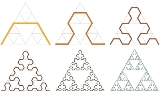
Sierpinski arrowhead curve
Encyclopedia
The Sierpiński arrowhead curve is a fractal curve similar in appearance and identical in limit to the Sierpiński triangle
.
(L-system
).
Here, F means “draw forward”, + means “turn left 60°”, and − means “turn right 60°” (see turtle graphics
).
Like many two-dimensional fractal curves, the Sierpiński arrowhead curve can be extended to three dimensions:

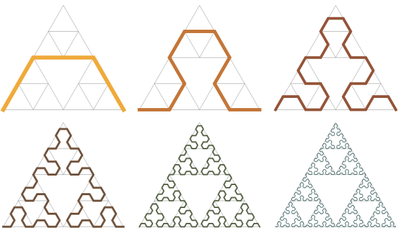
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
.

Representation as Lindenmayer system
The Sierpiński arrowhead curve can be expressed by a rewrite systemRewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
(L-system
L-system
An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
).
- Alphabet: X, Y
- Constants: F, +, −
- Axiom: XF
- Production rules:
- X → YF + XF + Y
- Y → XF − YF − X
Here, F means “draw forward”, + means “turn left 60°”, and − means “turn right 60°” (see turtle graphics
Turtle graphics
Turtle graphics is a term in computer graphics for a method of programming vector graphics using a relative cursor upon a Cartesian plane...
).
Like many two-dimensional fractal curves, the Sierpiński arrowhead curve can be extended to three dimensions:

Literature
- Peitgen et al., Chaos and Fractals, Springer-Verlag, 1992.
- Roger T. Stevens, Fractal Programming in C, M&T Books, 1989.
See also
- List of fractals by Hausdorff dimension
- Sierpiński curveSierpinski curveSierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit n \rightarrow \infty completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling...

