Koch snowflake - AbsoluteAstronomy.com

The Koch snowflake is a mathematical

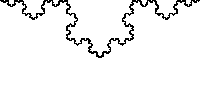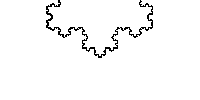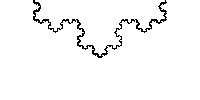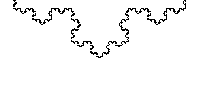
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

and one of the earliest fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

curves to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire") by the Swedish

Sweden

Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....

mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

Helge von Koch

Niels Fabian Helge von Koch was a Swedish mathematician who gave his name to the famous fractal known as the Koch snowflake, one of the earliest fractal curves to be described....

Construction

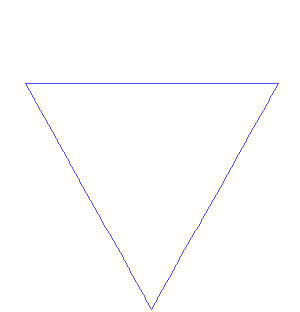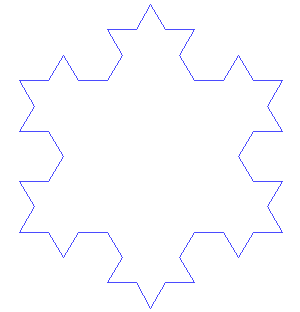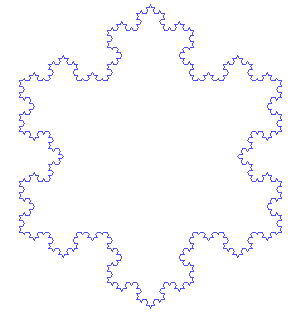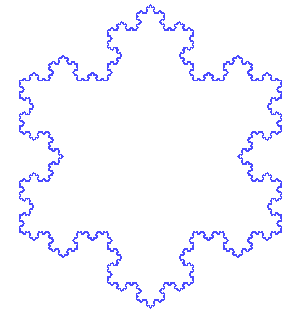
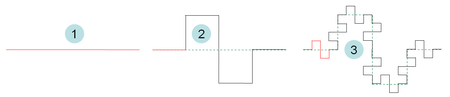
The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows:

divide the line segment into three segments of equal length.
draw an equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...

triangle that has the middle segment from step 1 as its base and points outward.
remove the line segment that is the base of the triangle from step 2.

After one iteration of this process, the resulting shape is the outline of a hexagram.

The Koch snowflake is the limit approached as the above steps are followed over and over again. The Koch curve originally described by Koch

Helge von Koch

Niels Fabian Helge von Koch was a Swedish mathematician who gave his name to the famous fractal known as the Koch snowflake, one of the earliest fractal curves to be described....

is constructed with only one of the three sides of the original triangle. In other words, three Koch curves make a Koch snowflake.

Properties

The Koch curve has an infinite length because each time the steps above are performed on each line segment of the figure there are four times as many line segments, the length of each being one-third the length of the segments in the previous stage. Hence, the total length increases by one third and thus the length at step n will be (4/3)ⁿ of the original triangle perimeter: the fractal dimension

Fractal dimension

In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...

is log 4/log 3 ≈ 1.26, greater than the dimension of a line (1) but less than Peano's space-filling curve

Space-filling curve

In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...

(2).

The Koch curve is continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

everywhere but differentiable

Differentiable function

In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...

nowhere.

Taking s as the side length, the original triangle area is

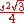. The side length of each successive small triangle is 1/3 of those in the previous iteration; because the area of the added triangles is proportional to the square of its side length, the area of each triangle added in the nth step is 1/9 of that in the (n-1)th step. In each iteration after the first, 4 times as many triangles are added as in the previous iteration; because the first iteration adds 3 triangles then the nth iteration will add

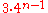triangles. Combining these two formulae gives the iteration formula: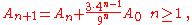

where

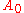is area of the original triangle. Substituting in

and expanding yields:

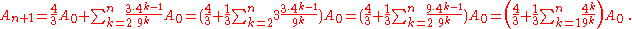
In the limit, as n goes to infinity, the limit of the sum of the powers of 4/9 is 4/5, so

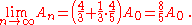
So the area of a Koch snowflake is 8/5 of the area of the original triangle, or

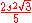. Therefore the infinite perimeter of the Koch triangle encloses a finite area.
It is possible to tessellate the plane by copies of Koch snowflakes in two different sizes. However, such a tessellation is not possible using only snowflakes of the same size as each other. Since each Koch snowflake in the tesselation can be subdivided into seven smaller snowflakes of two different sizes, it is also possible to find tessellations that use more than two sizes at once.

Thue-Morse Sequence and Turtle graphics

A Turtle Graphic

Turtle graphics

Turtle graphics is a term in computer graphics for a method of programming vector graphics using a relative cursor upon a Cartesian plane...

is the curve that is generated if an automaton is programmed with a sequence.
If the Thue–Morse sequence

Thue–Morse sequence

In mathematics, the Thue–Morse sequence, or Prouhet–Thue–Morse sequence, is a binary sequence that begins:Any other ordered pair of symbols may be used instead of 0 and 1; the logical structure of the Thue–Morse sequence does not depend on the symbols that are used to represent it.- Direct...

members are used in order to select program states:

If t(n) = 0, move ahead by one unit,
If t(n) = 1, rotate counterclockwise by an angle of π/3,

the resulting curve converges to the Koch snowflake.

Representation as Lindenmayer system

The Koch Curve can be expressed by a rewrite system (Lindenmayer system).

Alphabet : F

Constants : +, −

Axiom : F++F++F

Production rules:

F → F−F++F−F

Here, F means "draw forward", + means "turn right 60°", and − means "turn left 60°".

Variants of the Koch curve

Following von Koch's concept, several variants of the Koch curve were designed, considering right angles (quadratic), other angles (Césaro) or circles and their extensions to higher dimensions (Sphereflake):

Variant	Illustration	Construction
1D, 85° angle		The Cesaro fractal is a variant of the Koch curve with an angle between 60° and 90° (here 85°).
1D, 90° angle
1D, 90° angle
2D, triangles
2D, 90° angle		Extension of the quadratic type 1 curve. The illustration at left shows the fractal after the second iteration .
2D, 90° angle		Extension of the quadratic type 2 curve. The illustration at left shows the fractal after the first iteration.
2D, spheres		Eric Haines Eric Haines Eric Haines is an United States software engineer, expert in computer graphics, specifically in image rendering. he is with Autodesk, Inc., lead software engineer. He is a co-author of the book Real-Time Rendering.Eric Haines earned M.S... has developed the sphereflake fractal, which is a three-dimensional version of the Koch snowflake, using spheres.

External links