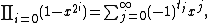Thue–Morse sequence
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Thue–Morse sequence, or Prouhet–Thue–Morse sequence, is a binary sequence that begins:
- 0 1 10 1001 10010110 1001011001101001....
Any other ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of symbols may be used instead of 0 and 1; the logical structure of the Thue–Morse sequence does not depend on the symbols that are used to represent it.
Direct definition
To compute the nth element tn, write the number n in binary. If the number of ones in this binary expansion is odd then tn = 1, if even then tn = 0. For this reason John H. Conway et al. call numbers n satisfying tn = 1 odious numbers and numbers for which tn = 0 evil numbers.Recurrence relation
The Thue–Morse sequence is the sequence tn satisfying| t0 | = 0, |
| t2n | = tn, and |
| t2n+1 | = 1−tn. |
for all positive integers n.
L-system
The Thue–Morse sequence is the output of the following Lindenmayer system:variables 0 1
constants none
start 0
rules (0 → 01), (1 → 10)
Characterization using bitwise negation
The Thue–Morse sequence in the form given above, as a sequence of bitBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s, can be defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
using the operation of bitwise negation.
So, the first element is 0.
Then once the first 2n elements have been specified, forming a string s, then the next 2n elements must form the bitwise negation of s.
Now we have defined the first 2n+1 elements, and we recurse.
Spelling out the first few steps in detail:
- We start with 0.
- The bitwise negation of 0 is 1.
- Combining these, the first 2 elements are 01.
- The bitwise negation of 01 is 10.
- Combining these, the first 4 elements are 0110.
- The bitwise negation of 0110 is 1001.
- Combining these, the first 8 elements are 01101001.
- And so on.
So
- T0 = 0.
- T1 = 01.
- T2 = 0110.
- T3 = 01101001.
- T4 = 0110100110010110.
- T5 = 01101001100101101001011001101001.
- T6 = 0110100110010110100101100110100110010110011010010110100110010110.
- And so on.
Infinite product
The sequence can also be defined by:where tj is the jth element if we start at j = 0.
Some properties

That is, there are many instances of XX, where X is some string.
However, there are no cubes: instances of XXX.
There are also no overlapping squares: instances of 0X0X0 or 1X1X1.
Notice that T2n is palindrome
Palindromic number
A palindromic number or numeral palindrome is a 'symmetrical' number like 16461, that remains the same when its digits are reversed. The term palindromic is derived from palindrome, which refers to a word like rotor that remains unchanged under reversal of its letters...
for any n > 1. Further, let qn be a word obtain from T2n by counting ones between consecutive zeros. For instance, q1 = 2 and q2 = 2102012 and so on. The words Tn do not contain overlapping squares in consequence, the words qn are palindrome squarefree words.
The statement above that the Thue–Morse sequence is "filled with squares" can be made precise:
It is a recurrent sequence, meaning that given any finite string X in the sequence, there is some length nX (often much longer than the length of X) such that X appears in every block of length n.
The easiest way to make a recurrent sequence is to form a periodic sequence
Periodic sequence
In mathematics, a periodic sequence is a sequence for which the same terms are repeated over and over:The number p of repeated terms is called the period.-Definition:A periodic sequence is a sequence a1, a2, a3, ... satisfying...
, one where the sequence repeats entirely after a given number m of steps.
Then nX can be set to any multiple of m that is larger than twice the length of X.
But the Morse sequence is recurrent without being periodic, not even eventually periodic (meaning periodic after some nonperiodic initial segment).
One can define a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f from the set of binary sequences to itself by replacing every 0 in a sequence with 01 and every 1 with 10.
Then if T is the Thue–Morse sequence, then f(T) is T again; that is, T is a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of f.
In fact, T is essentially the only fixed point of f; the only other fixed point is the bitwise negation of T, which is simply the Thue–Morse sequence on (1,0) instead of on (0,1).
This property may be generalized to the concept of an automatic sequence
Automatic sequence
An automatic sequence is an infinite sequence of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k...
.
In combinatorial game theory
The set of evil numbers (numbers with
with 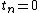 ) forms a subspace of the nonnegative integers under nim-addition (bitwise
) forms a subspace of the nonnegative integers under nim-addition (bitwiseBitwise operation
A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
exclusive or). For the game of Kayles
Kayles
In combinatorial game theory, Kayles is a simple impartial game. In the notation of octal games, Kayles is denoted 0.77.- Rules :Kayles is played with a row of tokens, which represent bowling pins. The row may be of any length...
, the evil numbers form the sparse space—the subspace of nim-values which occur for few (finitely many) positions in the game—and the odious numbers are the common coset.
The Prouhet–Tarry–Escott problem
The Prouhet–Tarry–Escott problem can be defined as: given a positive integer N and a non-negative integer k, partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
the set S = { 0, 1, ..., N-1 } into two disjoint subsets S0 and S1 that have equal sums of powers up to k, that is:
 for all integers i from 1 to k.
for all integers i from 1 to k.This has a solution if N is a multiple of 2k+1, given by:
- S0 consists of the integers n in S for which tn = 0,
- S1 consists of the integers n in S for which tn = 1.
For example, for N = 8 and k = 2,
The condition requiring that N be a multiple of 2k+1 is not strictly necessary: there are some further cases for which a solution exists. However, it guarantees a stronger property: if the condition is satisfied, then the set of kth powers of any set of N numbers in arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
can be partitioned into two sets with equal sums. This follows directly from the expansion given by the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
applied to the binomial representing the nth element of an arithmetic progression.
Fractals and Turtle graphics
A Turtle GraphicsTurtle graphics
Turtle graphics is a term in computer graphics for a method of programming vector graphics using a relative cursor upon a Cartesian plane...
is the curve that is generated if an automaton is programmed with a sequence.
If the Thue–Morse Sequence members are used in order to select program states:
- If t(n) = 0, move ahead by one unit,
- If t(n) = 1, rotate counterclockwise by an angle of π/3,
the resulting curve converges to the Koch snowflake
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
, a fractal curve of
infinite length containing a finite area. This illustrates the fractal nature of the Thue–Morse Sequence.
History
The Thue–Morse sequence was first studied by Eugène Prouhet in 1851, who applied it to number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
However, Prouhet did not mention the sequence explicitly; this was left to Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
in 1906, who used it to found the study of combinatorics on words
Combinatorics on words
Combinatorics on words is a branch of mathematics which applies combinatorics to words and formal languages. The study of combinatorics on words arose independently within several branches of mathematics, e.g. number theory, group theory and probability...
.
The sequence was only brought to worldwide attention with the work of Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
in 1921, when he applied it to differential geometry.
The sequence has been discovered independently many times, not always by professional research mathematicians; for example, Max Euwe
Max Euwe
Machgielis Euwe was a Dutch chess Grandmaster, mathematician, and author. He was the fifth player to become World Chess Champion . Euwe also served as President of FIDE, the World Chess Federation, from 1970 to 1978.- Early years :Euwe was born in Watergraafsmeer, near Amsterdam...
, a chess grandmaster, who held the world championship title from 1935 to 1937, and mathematics teacher
Teacher
A teacher or schoolteacher is a person who provides education for pupils and students . The role of teacher is often formal and ongoing, carried out at a school or other place of formal education. In many countries, a person who wishes to become a teacher must first obtain specified professional...
, discovered it in 1929 in an application to chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
: by using its cube-free property (see above), he showed how to circumvent a rule aimed at preventing infinitely protracted games by declaring repetition of moves a draw.
External links
- Allouche, J.-P.; Shallit, J. O. The Ubiquitous Prouhet-Thue-Morse Sequence. (contains many applications and some history)
- Thue–Morse Sequence over (1,2)
- Odious numbers
- Evil numbers
- When Thue-Morse meets Koch. A paper showing an astonishing similarity between the Thue–Morse Sequence and the Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
- Reducing the influence of DC offset drift in analog IPs using the Thue-Morse Sequence. A technical application of the Thue–Morse Sequence
- MusiNum - The Music in the Numbers. Freeware to generate self similar music based on the Thue–Morse Sequence and related number sequences.