
Automatic sequence
Encyclopedia
An automatic sequence is an infinite sequence
of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k. A k-automatic set is a set of non-negative integers for which the sequence of values of its characteristic function is an automatic sequence: that is, membership of n in the set can be determined by a finite state automaton on the digits of n in base k.
, and A = (E, φ, e) be a deterministic automaton where
also let A be a finite set, and π:E → A a projection
towards A.
For each n, take m(n) = π(φ(e, )) where
)) where  is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.
is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.
of the free monoid E* with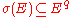 , and
, and  such that σ(e) begins by e. Let also be A and π as before. Then if
such that σ(e) begins by e. Let also be A and π as before. Then if  is a fixpoint of σ, that is to say
is a fixpoint of σ, that is to say  = σ(
= σ( ), then m = π(
), then m = π( ) is a q-automatic sequence over A.
) is a q-automatic sequence over A.
for n, that is (1)n. Since a finite state automaton must eventually return to a previously visited state, all 1-automatic sequences are eventually periodic.
for which the base-b expansion is an automatic sequence. It is conjectured that all such numbers are either rational
or transcendental
.
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k. A k-automatic set is a set of non-negative integers for which the sequence of values of its characteristic function is an automatic sequence: that is, membership of n in the set can be determined by a finite state automaton on the digits of n in base k.
Automaton point of view
Let q be an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, and A = (E, φ, e) be a deterministic automaton where
- E is the finite set of stateState (computer science)In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
s - φ : E×[0,q − 1] → E is the transition function
 is the initial state
is the initial state
also let A be a finite set, and π:E → A a projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
towards A.
For each n, take m(n) = π(φ(e,
 )) where
)) where  is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.
is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.Substitution point of view
Let σ be a morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
of the free monoid E* with
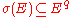 , and
, and  such that σ(e) begins by e. Let also be A and π as before. Then if
such that σ(e) begins by e. Let also be A and π as before. Then if  is a fixpoint of σ, that is to say
is a fixpoint of σ, that is to say  = σ(
= σ( ), then m = π(
), then m = π( ) is a q-automatic sequence over A.
) is a q-automatic sequence over A.1-automatic sequences
k-automatic sequences are normally only defined for k ≥ 2. The concept can be extended to k = 1 by defining a 1-automatic sequence to be a sequence whose n-th term depends on the unary notationUnary numeral system
The unary numeral system is the bijective base-1 numeral system. It is the simplest numeral system to represent natural numbers: in order to represent a number N, an arbitrarily chosen symbol representing 1 is repeated N times. For example, using the symbol | , the number 6 is represented as ||||||...
for n, that is (1)n. Since a finite state automaton must eventually return to a previously visited state, all 1-automatic sequences are eventually periodic.
Properties
For given k and r, a set is k-automatic if and only if it is kr-automatic. Otherise, if h and k are multiplicatively independent, then a set is both h-automatic and k-automatic if and only if it is 1-automatic, that is, ultimately periodic.Examples
The following sequences are automatic:- Thue-Morse sequenceThue-Morse sequenceIn mathematics, the Thue–Morse sequence, or Prouhet–Thue–Morse sequence, is a binary sequence that begins:Any other ordered pair of symbols may be used instead of 0 and 1; the logical structure of the Thue–Morse sequence does not depend on the symbols that are used to represent it.- Direct...
: take E = A = {0, 1}, e = 0, π = id, and σ such that σ(0) = 01, σ(1) = 10; we get the fixpoint 01101001100101101001011001101001... , which is in fact the Thue-Morse word. The n-th term is the parity of the base 2 representation of n and the sequence is thus 2-automatic. - Rudin–Shapiro sequenceRudin–Shapiro sequenceIn mathematics the Rudin–Shapiro sequence, also known as the Golay–Rudin–Shapiro sequence is an infinite automatic sequence named after Marcel Golay, Walter Rudin and Harold S. Shapiro, who independently investigated its properties.-Definition:...
- Baum–Sweet sequenceBaum–Sweet sequenceIn mathematics the Baum–Sweet sequence is an infinite automatic sequence of 0s and 1s defined by the rule:for n ≥ 0.For example, b4 = 1 because the binary representation of 4 is 100, which only contains one block of consecutive 0s of length 2; whereas b5 = 0 because the binary representation of...
- Regular paperfolding sequenceRegular paperfolding sequenceIn mathematics the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite automatic sequence of 0s and 1s defined as the limit of the following process:...
Automatic real number
An automatic real number is a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
for which the base-b expansion is an automatic sequence. It is conjectured that all such numbers are either rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
or transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.

