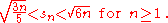Rudin–Shapiro sequence
Encyclopedia
In mathematics
the Rudin–Shapiro sequence, also known as the Golay–Rudin–Shapiro sequence is an infinite automatic sequence
named after Marcel Golay, Walter Rudin
and Harold S. Shapiro
, who independently investigated its properties.


where the εi are the digits in the binary expansion of n. Thus an counts the number of (possibly overlapping) occurrences of the sub-string 11 in the binary expansion of n, and bn is +1 if an is even and −1 if an is odd.
For example, a6 = 1 and b6 = −1 because the binary representation of 6 is 110, which contains one occurrence of 11; whereas a7 = 2 and b7 = +1 because the binary representation of 7 is 111, which contains two (overlapping) occurrences of 11.
Starting at n = 0, the first few terms of the an sequence are:
and the corresponding terms bn of the Rudin–Shapiro sequence are:
.
The values of the terms an and bn in the Rudin–Shapiro sequence can be found recursively as follows. If n = m.2k where m is odd then
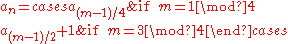
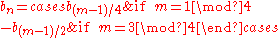
Thus a108 = a13 + 1 = a3 + 1 = a1 + 2 = a0 + 2 = 2, which can be verified by observing that the binary representation of 108, which is 1101100, contains two sub-strings 11. And so b108 = (−1)2 = +1.
The Rudin-Shapiro word +1 +1 +1 −1 +1 +1 −1 +1 +1 +1 +1 −1 −1 −1 +1 −1 ..., which is created by concatenating the terms of the Rudin–Shapiro sequence, is a fixed point of the morphism or string substitution rules
as follows:
It can be seen from the morphism rules that the Rudin–Shapiro string contains at most four consecutive +1s and at most four consecutive −1s.
The sequence of partial sums of the Rudin–Shapiro sequence, defined by

with values
can be shown to satisfy the inequality
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Rudin–Shapiro sequence, also known as the Golay–Rudin–Shapiro sequence is an infinite automatic sequence
Automatic sequence
An automatic sequence is an infinite sequence of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k...
named after Marcel Golay, Walter Rudin
Walter Rudin
Walter Rudin was an American mathematician, for most of his career a Professor of Mathematics at the University of Wisconsin–Madison....
and Harold S. Shapiro
Harold S. Shapiro
Harold Seymour Shapiro is a professor emeritus of mathematics at the Royal Institute of Technology in Stockholm, Sweden, best...
, who independently investigated its properties.
Definition
Each term of the Rudin-Shapiro sequence is either +1 or −1. The nth term of the sequence, bn, is defined by the rules:

where the εi are the digits in the binary expansion of n. Thus an counts the number of (possibly overlapping) occurrences of the sub-string 11 in the binary expansion of n, and bn is +1 if an is even and −1 if an is odd.
For example, a6 = 1 and b6 = −1 because the binary representation of 6 is 110, which contains one occurrence of 11; whereas a7 = 2 and b7 = +1 because the binary representation of 7 is 111, which contains two (overlapping) occurrences of 11.
Starting at n = 0, the first few terms of the an sequence are:
- 0, 0, 0, 1, 0, 0, 1, 2, 0, 0, 0, 1, 1, 1, 2, 3, ...
and the corresponding terms bn of the Rudin–Shapiro sequence are:
- +1, +1, +1, −1, +1, +1, −1, +1, +1, +1, +1, −1, −1, −1, +1, −1, ...
Properties
The Rudin–Shapiro sequence can be generated by a four state automatonFinite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
.
The values of the terms an and bn in the Rudin–Shapiro sequence can be found recursively as follows. If n = m.2k where m is odd then
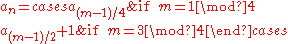
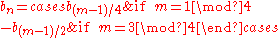
Thus a108 = a13 + 1 = a3 + 1 = a1 + 2 = a0 + 2 = 2, which can be verified by observing that the binary representation of 108, which is 1101100, contains two sub-strings 11. And so b108 = (−1)2 = +1.
The Rudin-Shapiro word +1 +1 +1 −1 +1 +1 −1 +1 +1 +1 +1 −1 −1 −1 +1 −1 ..., which is created by concatenating the terms of the Rudin–Shapiro sequence, is a fixed point of the morphism or string substitution rules
- +1 +1 → +1 +1 +1 −1
- +1 −1 → +1 +1 −1 +1
- −1 +1 → −1 −1 +1 −1
- −1 −1 → −1 −1 −1 +1
as follows:
- +1 +1 → +1 +1 +1 −1 → +1 +1 +1 −1 +1 +1 −1 +1 → +1 +1 +1 −1 +1 +1 −1 +1 +1 +1 +1 −1 −1 −1 +1 −1 ...
It can be seen from the morphism rules that the Rudin–Shapiro string contains at most four consecutive +1s and at most four consecutive −1s.
The sequence of partial sums of the Rudin–Shapiro sequence, defined by

with values
- 1, 2, 3, 2, 3, 4, 3, 4, 5, 6, 7, 6, 5, 4, 5, 4, ...
can be shown to satisfy the inequality