
Regular paperfolding sequence
Encyclopedia
In mathematics
the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite automatic sequence
of 0s and 1s defined as the limit of the following process:
At each stage an alternating sequence of 1s and 0s is inserted between the terms of the previous sequence. The sequence takes its name from the fact that it represents the sequence of left and right folds along a strip of paper that is folded repeatedly in half in the same direction. If each fold is then opened out to create right angled corner, the resulting shape approaches the dragon curve
fractal.
 Starting at n = 1, the first few terms of the regular paperfolding sequence are:
Starting at n = 1, the first few terms of the regular paperfolding sequence are:
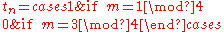
Thus t12 = t3 = 0 but t13 = 1.
The paperfolding word 1101100111001001..., which is created by concatenating the terms of the regular paperfolding sequence, is a fixed point of the morphism or string substitution rules
as follows:
It can be seen from the morphism rules that the paperfolding word contains at most three consecutive 0s and at most three consecutive 1s.
The paperfolding sequence also satisfies the symmetry relation:
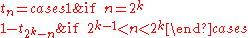
which shows that the paperfolding word can be constructed as the limit of another iterated process as follows:
In each iteration of this process, a 1 is placed at the end of the previous iteration's string, then this string is repeated in reverse order, replacing 0 by 1 and vice versa.

From the construction of the paperfolding sequence it can be seen that G satisfies the functional relation

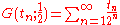
This number is known as the paperfolding constant and has the value

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite automatic sequence
Automatic sequence
An automatic sequence is an infinite sequence of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k...
of 0s and 1s defined as the limit of the following process:
- 1
- 1 1 0
- 1 1 0 1 1 0 0
- 1 1 0 1 1 0 0 1 1 1 0 0 1 0 0
At each stage an alternating sequence of 1s and 0s is inserted between the terms of the previous sequence. The sequence takes its name from the fact that it represents the sequence of left and right folds along a strip of paper that is folded repeatedly in half in the same direction. If each fold is then opened out to create right angled corner, the resulting shape approaches the dragon curve
Dragon curve
A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
fractal.

- 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, ...
Properties
The value of any given term tn in the regular paperfolding sequence can be found recursively as follows. If n = m·2k where m is odd then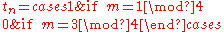
Thus t12 = t3 = 0 but t13 = 1.
The paperfolding word 1101100111001001..., which is created by concatenating the terms of the regular paperfolding sequence, is a fixed point of the morphism or string substitution rules
- 11 → 1101
- 01 → 1001
- 10 → 1100
- 00 → 1000
as follows:
- 11 → 1101 → 11011001 → 1101100111001001 → 11011001110010011101100011001001 ...
It can be seen from the morphism rules that the paperfolding word contains at most three consecutive 0s and at most three consecutive 1s.
The paperfolding sequence also satisfies the symmetry relation:
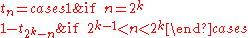
which shows that the paperfolding word can be constructed as the limit of another iterated process as follows:
- 1
- 1 1 0
- 110 1 100
- 1101100 1 1100100
- 110110011100100 1 110110001100100
In each iteration of this process, a 1 is placed at the end of the previous iteration's string, then this string is repeated in reverse order, replacing 0 by 1 and vice versa.
Generating function
The generating function of the paperfolding sequence is given by
From the construction of the paperfolding sequence it can be seen that G satisfies the functional relation

Paperfolding constant
Substituting x = ½ into the generating function gives a real number between 0 and 1 whose binary expansion is the paperfolding word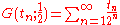
This number is known as the paperfolding constant and has the value


