Fractal dimension - AbsoluteAstronomy.com

In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal dimensions are the Rényi dimension, the Hausdorff dimension

Hausdorff dimension

thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...

and packing dimension

Packing dimension

In mathematics, the packing dimension is one of a number of concepts that can be used to define the dimension of a subset of a metric space. Packing dimension is in some sense dual to Hausdorff dimension, since packing dimension is constructed by "packing" small open balls inside the given subset,...

. Practically, the box-counting dimension and correlation dimension

Correlation dimension

In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension....

are widely used, partly due to their ease of implementation. In a box counting algorithm the number of boxes covering the point set is a power law

Power law

A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...

function of the box size. Fractal dimension is estimated as the exponent of such power law. Although for some classical fractals all these dimensions do coincide, in general they are not equivalent.

One non-trivial example is the fractal dimension of a Koch snowflake

Koch snowflake

The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...

. It has a topological dimension, but it is by no means a rectifiable curve: the length of the curve

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

between any two points on the Koch Snowflake is infinite. No small piece of it is line-like, but rather is composed of an infinite number of segments joined at different angles. The fractal dimension of a curve can be explained intuitively thinking of a fractal line as an object too big to be a one-dimensional object, but too thin to be a two-dimensional object. Therefore its dimension might best be described in a sense by the fractal dimension, which is a number between one and two.

Specific definitions

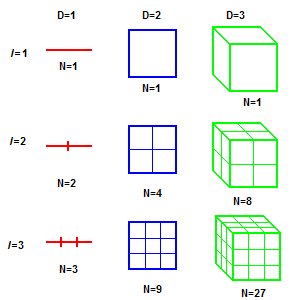
There are two main approaches to generate a fractal structure. One is growing from a unit object (Fig. 1), and the other is to construct the subsequent divisions of an original structure, like the Sierpinski triangle

Sierpinski triangle

The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...

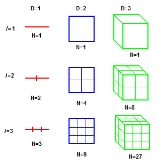
(Fig.2). Here we follow the second approach to define the dimension of fractal structures (See figure 1).

If we take an object with linear size equal to 1 residing in Euclidean dimension

, and reduce its linear size by the factor

in each spatial direction, it takes

number of self similar objects to cover the original object(Fig.(1)). However, the dimension defined by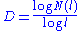

(where the logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

can be of any base) is still equal to its topological or Euclidean dimension. By applying the above equation to fractal structure, we can get the dimension of fractal structure (which Hausdorff proved being identical to the Hausdorff dimension

Hausdorff dimension

) as a non-whole number as expected.

where (ε) is the number of self-similar structures of linear size ε
needed to cover the whole structure.

For instance, the fractal dimension of the Sierpinski triangle (Fig.(2)) is given by,

Closely related to this is the box-counting dimension, which considers, if the space were divided up into a grid of boxes of size ε, how many boxes of that scale would contain part of the attractor

Attractor

An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...

? Again,

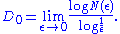
Other dimension quantities include the information dimension, which considers how the average information

Information entropy

In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...

needed to identify an occupied box scales, as the scale of boxes gets smaller:

and the correlation dimension

Correlation dimension

In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension....

, which is perhaps easiest to calculate,

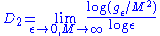
where M is the number of points used to generate a representation of the fractal or attractor, and g_ε is the number of pairs of points closer than ε to each other.

Rényi dimensions

The box-counting, information, and correlation dimensions, can be seen as special cases of a continuous spectrum of generalised or Rényi dimensions of order α, defined by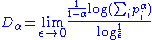

where the numerator in the limit is the Rényi entropy

Rényi entropy

In information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system...

of order α. The Rényi dimension with α=0 treats all parts of the support of the attractor equally; but for larger values of α increasing weight in the calculation is given to the parts of the attractor which are visited most frequently.

An attractor for which the Rényi dimensions are not all equal is said to be a multifractal, or to exhibit multifractal structure. This is a signature that different scaling behaviour is occurring in different parts of the attractor.

Estimating the fractal dimension of real-world data

The fractal dimension measures, described above, are derived from fractals which are formally-defined. However, organisms and real-world phenomena exhibit fractal properties (see Fractals in nature), so it can often be useful to characterise the fractal dimension of a set of sampled

Sample (statistics)

In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...

data. The fractal dimension measures cannot be derived exactly but must be estimated. This is used in a variety of research areas including physics, image analysis, acoustics, Riemann zeta zeros and even (electro)chemical processes.

Practical dimension estimates are very sensitive to numerical or experimental noise, and particularly sensitive to limitations on the amount of data. One should be cautious about claims based on fractal dimension estimates, particularly claims of low-dimensional dynamical behaviour — there is an inevitable ceiling, unless very large numbers of data points are presented. However, modelling as a multiplicative cascade

Multiplicative Cascade

In mathematics, a multiplicative cascade is a fractal/multifractal distribution of points produced via an iterative and multiplicative random process.Model I :Model II :Model III :...

leads to estimation of multifractal properties for relatively small datasets : a maximum likelihood fit of a multiplicative cascade to the dataset not only estimates the complete Renyi dimensions, but also gives reasonable estimates of the errors (see the web service http://www.maths.adelaide.edu.au/anthony.roberts/multifractal.php).

External links

http://www.trusoft-international.com TruSoft's Benoit - Fractal Analysis Software product calculates fractal dimensions and hurst exponents.
http://www.stevec.org/fracdim/ Fractal Dimension Estimator Java Applet

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.