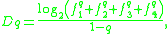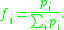Multiplicative Cascade
Encyclopedia
In mathematics, a multiplicative cascade is a fractal
/multifractal distribution of points produced via an iterative and multiplicative random process.
Model I (left plot):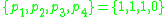
Model II (middle plot):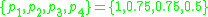
Model III (right plot):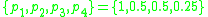
The plots above are examples of multiplicative cascade multifractals.
To create these distributions there are a few steps to take. Firstly, we must create a lattice of points which will be our underlying probability density field. Then we will populate this lattice with randomly placed points, insisting that the probability that the points be placed are proportional to the cell probability.
The fractal is constructed as follows: The space is split into four equal parts. Each part is then assigned a probability from the set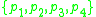
without replacement, where 
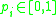. Each subspace is then divided again and assigned probabilities randomly from the same set and this is continued to the Nth level.
At the Nth level the probability of a cell being occupied is the product of the cell's pi and its parents and ancestors up to level 1 i.e. all the cells above it. In constructing this model down to level 8 we produce a 48 array of cells each with its own probability. To then place particle in the space we invoke a Monte Carlo rejection scheme
. Choosing x and y coordinates randomly we simply test if a random number between 0 and 1 is less or greater than the cell probability. To produce the plots above we dust the probability density field with 5,000 points in a space of 256 × 256.
An example of the probability density field:
The fractals are generally not scale-invariant and therefore cannot be considered standard fractals. They can however be considered multifractals. The Renyi (generalized) dimensions can be theoretically predicted. It can be shown that as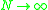
,
where N is the level of the grid refinement and,
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
/multifractal distribution of points produced via an iterative and multiplicative random process.
Model I (left plot):
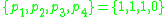
Model II (middle plot):
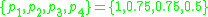
Model III (right plot):
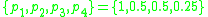
The plots above are examples of multiplicative cascade multifractals.
To create these distributions there are a few steps to take. Firstly, we must create a lattice of points which will be our underlying probability density field. Then we will populate this lattice with randomly placed points, insisting that the probability that the points be placed are proportional to the cell probability.
The fractal is constructed as follows: The space is split into four equal parts. Each part is then assigned a probability from the set
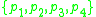without replacement, where 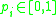. Each subspace is then divided again and assigned probabilities randomly from the same set and this is continued to the Nth level.At the Nth level the probability of a cell being occupied is the product of the cell's pi and its parents and ancestors up to level 1 i.e. all the cells above it. In constructing this model down to level 8 we produce a 48 array of cells each with its own probability. To then place particle in the space we invoke a Monte Carlo rejection scheme
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
. Choosing x and y coordinates randomly we simply test if a random number between 0 and 1 is less or greater than the cell probability. To produce the plots above we dust the probability density field with 5,000 points in a space of 256 × 256.
An example of the probability density field:
The fractals are generally not scale-invariant and therefore cannot be considered standard fractals. They can however be considered multifractals. The Renyi (generalized) dimensions can be theoretically predicted. It can be shown that as
,
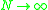where N is the level of the grid refinement and,
See also
- Fractal dimensionFractal dimensionIn fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
- Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
- Scale invarianceScale invarianceIn physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...