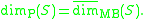Packing dimension
Encyclopedia
In mathematics
, the packing dimension is one of a number of concepts that can be used to define the dimension
of a subset
of a metric space
. Packing dimension is in some sense dual
to Hausdorff dimension
, since packing dimension is constructed by "packing" small open balls inside the given subset, whereas Hausdorff dimension is constructed by covering the given subset by such small open balls.
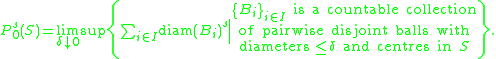
Unfortunately, this is just a pre-measure
and not a true measure
on subsets of X, as can be seen by considering dense
, countable
subsets. However, the pre-measure leads to a bona fide measure: the s-dimensional packing measure of S is defined to be
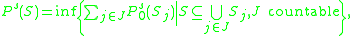
i.e., the packing measure of S is the infimum
of the packing pre-measures of countable covers of S.
Having done this, the packing dimension dimP(S) of S is defined analogously to the Hausdorff dimension:
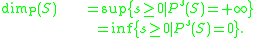
s more general than "diameter to the s": for any function h : [0, +∞) → [0, +∞], let the packing pre-measure of S with dimension function h be given by
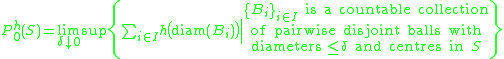
and define the packing measure of S with dimension function h by

The function h is said to be an exact (packing) dimension function for S if Ph(S) is both finite and strictly positive.
Note, however, that the packing dimension is not equal to the box dimension. For example, the set of rationals
Q has box dimension one and packing dimension zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the packing dimension is one of a number of concepts that can be used to define the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. Packing dimension is in some sense dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
, since packing dimension is constructed by "packing" small open balls inside the given subset, whereas Hausdorff dimension is constructed by covering the given subset by such small open balls.
Definitions
Let (X, d) be a metric space with a subset S ⊆ X and let s ≥ 0. The s-dimensional packing pre-measure of S is defined to be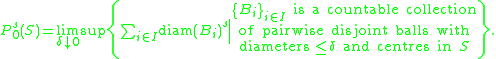
Unfortunately, this is just a pre-measure
Pre-measure
In mathematics, a pre-measure is a function that is, in some sense, a precursor to a bona fide measure on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory, where they can be used to define measures such as Hausdorff measure and packing measure on metric...
and not a true measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on subsets of X, as can be seen by considering dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
, countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
subsets. However, the pre-measure leads to a bona fide measure: the s-dimensional packing measure of S is defined to be
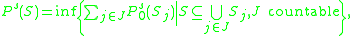
i.e., the packing measure of S is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the packing pre-measures of countable covers of S.
Having done this, the packing dimension dimP(S) of S is defined analogously to the Hausdorff dimension:
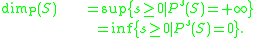
Generalizations
One can consider dimension functionDimension function
In mathematics, the notion of an dimension function is a tool in the study of fractals and other subsets of metric spaces...
s more general than "diameter to the s": for any function h : [0, +∞) → [0, +∞], let the packing pre-measure of S with dimension function h be given by
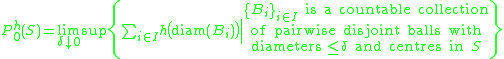
and define the packing measure of S with dimension function h by

The function h is said to be an exact (packing) dimension function for S if Ph(S) is both finite and strictly positive.
Properties
- If S is a subset of n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with its usual metric, then the packing dimension of S is equal to the upper modified box dimension of S:
- This result is interesting because it shows how a dimension derived from a measure (packing dimension) agrees with one derived without using a measure (the modified box dimension).
Note, however, that the packing dimension is not equal to the box dimension. For example, the set of rationals
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
Q has box dimension one and packing dimension zero.