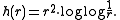Dimension function
Encyclopedia
In mathematics
, the notion of an (exact) dimension function (also known as a gauge function) is a tool in the study of fractal
s and other subsets of metric space
s. Dimension functions are a generalisation of the simple "diameter
to the dimension
" power law
used in the construction of s-dimensional Hausdorff measure
.
E of X. Given a number s ≥ 0, the s-dimensional Hausdorff measure of E, denoted μs(E), is defined by
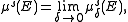
where
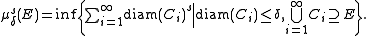
μδs(E) can be thought of as an approximation to the "true" s-dimensional area/volume of E given by calculating the minimal s-dimensional area/volume of a covering of E by sets of diameter at most δ.
As a function of increasing s, μs(E) is non-increasing. In fact, for all values of s, except possibly one, Hs(E) is either 0 or +∞; this exceptional value is called the Hausdorff dimension of E, here denoted dimH(E). Intuitively speaking, μs(E) = +∞ for s < dimH(E) for the same reason as the 1-dimensional linear length
of a 2-dimensional disc
in the Euclidean plane is +∞; likewise, μs(E) = 0 for s > dimH(E) for the same reason as the 3-dimensional volume
of a disc in the Euclidean plane is zero.
The idea of a dimension function is to use different functions of diameter than just diam(C)s for some s, and to look for the same property of the Hausdorff measure being finite and non-zero.
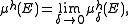
where
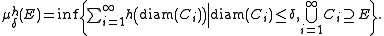
Then h is called an (exact) dimension function (or gauge function) for E if μh(E) is finite and strictly positive. There are many conventions as to the properties that h should have: Rogers (1998), for example, requires that h should be monotonically increasing for t ≥ 0, strictly positive for t > 0, and continuous
on the right for all t ≥ 0.
is constructed in a very similar way to Hausdorff dimension, except that one "packs" E from inside with pairwise disjoint balls of diameter at most δ. Just as before, one can consider functions h : [0, +∞) → [0, +∞] more general than h(δ) = δs and call h an exact dimension function for E if the h-packing measure of E is finite and strictly positive.
, a sample path X of Brownian motion
in the Euclidean plane has Hausdorff dimension equal to 2, but the 2-dimensional Hausdorff measure μ2(X) is zero. The exact dimension function h is given by the logarithm
ic correction
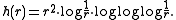
I.e., with probability one, 0 < μh(X) < +∞ for a Brownian path X in R2. For Brownian motion in Euclidean n-space Rn with n ≥ 3, the exact dimension function is
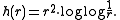
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of an (exact) dimension function (also known as a gauge function) is a tool in the study of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s and other subsets of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. Dimension functions are a generalisation of the simple "diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
to the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
" power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
used in the construction of s-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
.
Motivation: s-dimensional Hausdorff measure
Consider a metric space (X, d) and a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
E of X. Given a number s ≥ 0, the s-dimensional Hausdorff measure of E, denoted μs(E), is defined by
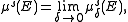
where
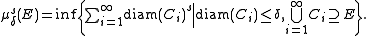
μδs(E) can be thought of as an approximation to the "true" s-dimensional area/volume of E given by calculating the minimal s-dimensional area/volume of a covering of E by sets of diameter at most δ.
As a function of increasing s, μs(E) is non-increasing. In fact, for all values of s, except possibly one, Hs(E) is either 0 or +∞; this exceptional value is called the Hausdorff dimension of E, here denoted dimH(E). Intuitively speaking, μs(E) = +∞ for s < dimH(E) for the same reason as the 1-dimensional linear length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
of a 2-dimensional disc
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
in the Euclidean plane is +∞; likewise, μs(E) = 0 for s > dimH(E) for the same reason as the 3-dimensional volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a disc in the Euclidean plane is zero.
The idea of a dimension function is to use different functions of diameter than just diam(C)s for some s, and to look for the same property of the Hausdorff measure being finite and non-zero.
Definition
Let (X, d) be a metric space and E ⊆ X. Let h : [0, +∞) → [0, +∞] be a function. Define μh(E) by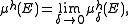
where
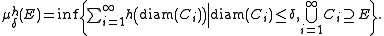
Then h is called an (exact) dimension function (or gauge function) for E if μh(E) is finite and strictly positive. There are many conventions as to the properties that h should have: Rogers (1998), for example, requires that h should be monotonically increasing for t ≥ 0, strictly positive for t > 0, and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the right for all t ≥ 0.
Packing dimension
Packing dimensionPacking dimension
In mathematics, the packing dimension is one of a number of concepts that can be used to define the dimension of a subset of a metric space. Packing dimension is in some sense dual to Hausdorff dimension, since packing dimension is constructed by "packing" small open balls inside the given subset,...
is constructed in a very similar way to Hausdorff dimension, except that one "packs" E from inside with pairwise disjoint balls of diameter at most δ. Just as before, one can consider functions h : [0, +∞) → [0, +∞] more general than h(δ) = δs and call h an exact dimension function for E if the h-packing measure of E is finite and strictly positive.
Example
Almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
, a sample path X of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
in the Euclidean plane has Hausdorff dimension equal to 2, but the 2-dimensional Hausdorff measure μ2(X) is zero. The exact dimension function h is given by the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic correction
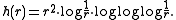
I.e., with probability one, 0 < μh(X) < +∞ for a Brownian path X in R2. For Brownian motion in Euclidean n-space Rn with n ≥ 3, the exact dimension function is