Lévy C curve
Encyclopedia
In mathematics
, the Lévy C curve is a self-similar fractal
that was first described and whose differentiability properties were analysed by Ernesto Cesàro
in 1906 and G. Farber in 1910, but now bears the name of French
mathematician
Paul Pierre Lévy
, who was the first to describe its self-similarity properties, as well as to provide a geometrical construction showing it as a representative curve in the same class as the Koch curve
. It is a special case of a period-doubling curve, a de Rham curve
.
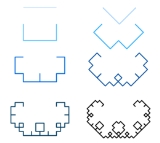
If using a Lindenmayer system then the construction of the C curve starts with a straight line. An isosceles triangle with angles of 45°, 90° and 45° is built using this line as its hypotenuse
. The original line is then replaced by the other two sides of this triangle.
At the second stage, the two new lines each form the base for another right-angled isosceles triangle, and are replaced by the other two sides of their respective triangle. So, after two stages, the curve takes the appearance of three sides of a rectangle with the same length as the original line, but only half as wide.
At each subsequent stage, each straight line segment in the curve is replaced by the other two sides of a right-angled isosceles triangle built on it. After n stages the curve consists of 2n line segments, each of which is smaller than the original line by a factor of 2n/2.
This L-system can be described as follows:
|Variables:||F
|-
|Constants:||+ −
|-
|Start:||F
|-
|Rules:||F → +F−−F+
|}
where "F" means "draw forward", "+" means "turn clockwise 45°", and "−" means "turn anticlockwise 45°".
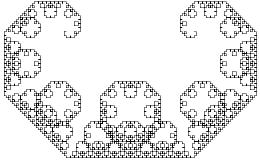
The fractal curve that is the limit of this "infinite" process is the Lévy C curve. It takes its name from its resemblance to a highly ornamented version of the letter "C". The curve resembles the finer details of the Pythagoras tree.
The Hausdorff dimension
of the C curve equals 2 (it contains open sets), whereas the boundary has dimension about 1.9340 http://mathworld.wolfram.com/LevyFractal.html.
.jpg)
If using an iterated function system
(IFS, or the chaos game
IFS-method actually), then the construction of the C curve is a bit easier. It will need a set of two "rules" which are: Two point
s in a plane
(the translators
), each associated with a scale factor
of 1/√2. The first rule is a rotation of 45° and the second −45°. This set will iterate a point [x, y] from randomly choosing any of the two rules and use the parameters associated with the rule to scale/rotate and translate the point using a 2D-transform
function.
Put into formulae:
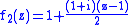
from the initial set of points
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lévy C curve is a self-similar fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
that was first described and whose differentiability properties were analysed by Ernesto Cesàro
Ernesto Cesàro
Ernesto Cesàro was an Italian mathematician who worked in the field of differential geometry.Cesàro was born in Naples. He is known also for his 'averaging' method for the summation of divergent series, known as the Cesàro mean.-Books by E. Cesaro:* * Ernesto Cesàro (March 12, 1859 – September...
in 1906 and G. Farber in 1910, but now bears the name of French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Paul Pierre Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
, who was the first to describe its self-similarity properties, as well as to provide a geometrical construction showing it as a representative curve in the same class as the Koch curve
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
. It is a special case of a period-doubling curve, a de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
.
L-system construction
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
. The original line is then replaced by the other two sides of this triangle.
At the second stage, the two new lines each form the base for another right-angled isosceles triangle, and are replaced by the other two sides of their respective triangle. So, after two stages, the curve takes the appearance of three sides of a rectangle with the same length as the original line, but only half as wide.
At each subsequent stage, each straight line segment in the curve is replaced by the other two sides of a right-angled isosceles triangle built on it. After n stages the curve consists of 2n line segments, each of which is smaller than the original line by a factor of 2n/2.
This L-system can be described as follows:
|Variables:||F
|-
|Constants:||+ −
|-
|Start:||F
|-
|Rules:||F → +F−−F+
|}
where "F" means "draw forward", "+" means "turn clockwise 45°", and "−" means "turn anticlockwise 45°".
The fractal curve that is the limit of this "infinite" process is the Lévy C curve. It takes its name from its resemblance to a highly ornamented version of the letter "C". The curve resembles the finer details of the Pythagoras tree.
The Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of the C curve equals 2 (it contains open sets), whereas the boundary has dimension about 1.9340 http://mathworld.wolfram.com/LevyFractal.html.
Variations
The standard C curve is built using 45° isosceles triangles. Variations of the C curve can be constructed by using isosceles triangles with angles other than 45°. As long as the angle is less than 60°, the new lines introduced at each stage are each shorter than the lines that they replace, so the construction process tends towards a limit curve. Angles less than 45° produce a fractal that is less tightly "curled".IFS construction
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
(IFS, or the chaos game
Chaos game
In mathematics, the term chaos game, as coined by Michael Barnsley, originally referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it...
IFS-method actually), then the construction of the C curve is a bit easier. It will need a set of two "rules" which are: Two point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s in a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
(the translators
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
), each associated with a scale factor
Scale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
of 1/√2. The first rule is a rotation of 45° and the second −45°. This set will iterate a point [x, y] from randomly choosing any of the two rules and use the parameters associated with the rule to scale/rotate and translate the point using a 2D-transform
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
function.
Put into formulae:
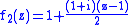
from the initial set of points
.
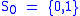