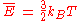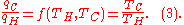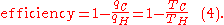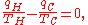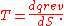Thermodynamic temperature
Encyclopedia
Thermodynamic temperature is the absolute measure of temperature
and is one of the principal parameters of thermodynamics
. Thermodynamic temperature is an "absolute" scale
because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero
, is the temperature at which the particle constituents of matter
have minimal motion and can become no colder.
At its simplest, temperature arises from the kinetic energy
of the vibrational motions of matter's
particle constituents (molecule
s, atom
s, and subatomic particle
s). The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, contribute the total thermal energy
(loosely, the heat
energy) within a substance. Thus, thermal energy may be stored in a number of ways within a substance, but only the kinetic energy of particles contributes to the substance's temperature.
. These motions comprise the kinetic
energy
in a substance. More specifically, the thermodynamic temperature of any bulk quantity of matter is the measure of the average kinetic energy of a certain kind of vibrational motion of its constituent particles called translational motions. Translational motions are ordinary, whole-body movements in three-dimensional space
whereby particles move about and exchange energy in collisions. Figure 1 below shows translational motion in gases; Figure 4 below shows translational motion in solids. Thermodynamic temperature's null
point, absolute zero, is the temperature at which the particle constituents of matter are as close as possible to complete rest; that is, they have minimal motion, retaining only quantum mechanical
motion. Zero kinetic energy remains in a substance at absolute zero (see Heat energy at absolute zero, below).
Throughout the scientific world where measurements are made in SI
units, thermodynamic temperature is measured in kelvin
s (symbol: K). Many engineering fields in the U.S.
however, measure thermodynamic temperature using the Rankine scale.
By international agreement, the unit kelvin and its scale are defined by two points: absolute zero, and the triple point
of Vienna Standard Mean Ocean Water (water with a specified blend of hydrogen and oxygen isotopes). Absolute zero, the lowest possible temperature, is defined as being precisely 0 K and −273.15 °C
. The triple point
of water is defined as being precisely 273.16 K and 0.01 °C. This definition does three things:
Temperatures expressed in kelvins are converted to degrees Rankine simply by multiplying by 1.8 as follows: T°R = 1.8TK, where TK and T°R are temperatures in kelvin and degrees Rankine respectively. Temperatures expressed in degrees Rankine are converted to kelvins by dividing by 1.8 as follows: TK = .
(known as SPRTs, PRTs or Platium RTDs) and monochromatic radiation thermometers
.
of the vibrational motions of matter's
particle constituents (molecule
s, atom
s, and subatomic particle
s). The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, contribute the total thermal energy
(loosely, the heat
energy) within a substance. Thus, thermal energy may be stored in a number of ways within a substance, but only the kinetic energy of particles contributes to the substance's temperature. The heat capacity
, which relates heat input and temperature change, is discussed below.
The relationship of kinetic energy, mass, and velocity is given by the formula Ek = mv2. Accordingly, particles with one unit of mass moving at one unit of velocity have precisely the same kinetic energy, and precisely the same temperature, as those with four times the mass but half the velocity.
The thermodynamic temperature of any bulk quantity of a substance (a statistically significant quantity of particles) is directly proportional to the mean average kinetic energy of a specific kind of particle motion known as translational motion. These simple movements in the three x, y, and z–axis dimensions of space means the particles move in the three spatial degrees of freedom
. This particular form of kinetic energy is sometimes referred to as kinetic temperature. Translational motion is but one form of heat energy and is what gives gases not only their temperature, but also their pressure and the vast majority of their volume. This relationship between the temperature, pressure, and volume of gases is established by the ideal gas law
's formula pV = nRT and is embodied in the gas laws
.
The extent to which the kinetic energy of translational motion of an individual atom or molecule (particle) in a gas contributes to the pressure and volume of that gas is a proportional function of thermodynamic temperature as established by the Boltzmann constant (symbol: kB). The Boltzmann constant also relates the thermodynamic temperature of a gas to the mean kinetic energy of an individual particle's translational motion as follows:
where:
While the Boltzmann constant is useful for finding the mean kinetic energy of a particle, it's important to note that even when a substance is isolated and in thermodynamic equilibrium
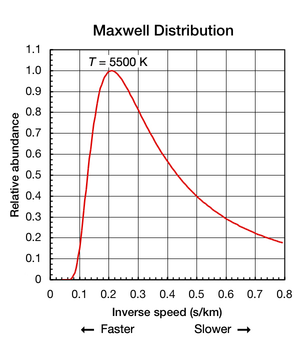
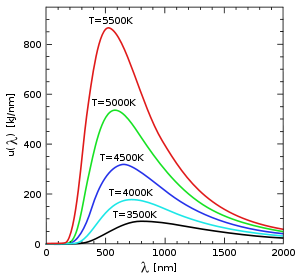
(all parts are at a uniform temperature and no heat is going into or out of it), the translational motions of individual atoms and molecules occurs across a wide range of speeds (see animation in Figure 1 above). At any one instant, the proportion of particles moving at a given speed within this range is determined by probability as described by the Maxwell–Boltzmann distribution. The graph shown here in Fig. 2 shows the speed distribution of 5500 K helium atoms. They have a most probable speed of 4.780 km/s. However, a certain proportion of atoms at any given instant are moving faster while others are moving relatively slowly; some are momentarily at a virtual standstill (off the x–axis to the right). This graph uses inverse speed for its x–axis so the shape of the curve can easily be compared to the curves in Figure 5 below. In both graphs, zero on the x–axis represents infinite temperature. Additionally, the x and y–axis on both graphs are scaled proportionally.
produces Brownian motion
that can be seen with an ordinary microscope. The translational motions of elementary particles are very fast and temperatures close to absolute zero are required to directly observe them. For instance, when scientists at the NIST
achieved a record-setting cold temperature of 700 nK (billionths of a kelvin) in 1994, they used optical lattice
laser equipment to adiabatically
cool caesium
atoms. They then turned off the entrapment lasers and directly measured atom velocities of 7 mm per second in order to calculate their temperature. Formulas for calculating the velocity and speed of translational motion are given in the following footnote.
There are other forms of heat energy besides the kinetic energy of translational motion. As can be seen in the animation at right, molecule
s are complex objects; they are a population of atoms and thermal agitation can strain their internal chemical bond
s in three different ways: via rotation, bond length, and bond angle movements. These are all types of internal degrees of freedom. This makes molecules distinct from monatomic substances (consisting of individual atoms) like the noble gas
es helium
and argon
, which have only the three translational degrees of freedom. Kinetic energy is stored in molecules' internal degrees of freedom, which gives them an internal temperature. Even though these motions are called internal, the external portions of molecules still move—rather like the jiggling of a stationary water balloon
. This permits the two-way exchange of kinetic energy between internal motions and translational motions with each molecular collision. Accordingly, as heat is removed from molecules, both their kinetic temperature (the kinetic energy of translational motion) and their internal temperature simultaneously diminish in equal proportions. This phenomenon is described by the equipartition theorem
, which states that for any bulk quantity of a substance in equilibrium, the kinetic energy of particle motion is evenly distributed among all the active degrees of freedom available to the particles. Since the internal temperature of molecules are usually equal to their kinetic temperature, the distinction is usually of interest only in the detailed study of non-local thermodynamic equilibrium (LTE) phenomena such as combustion
, the sublimation of solids, and the diffusion
of hot gases in a partial vacuum.
The kinetic energy stored internally in molecules causes substances to contain more heat energy at any given temperature and to absorb additional heat energy for a given temperature increase. This is because any kinetic energy that is, at a given instant, bound in internal motions is not at that same instant contributing to the molecules' translational motions. This extra kinetic energy simply increases the amount of heat energy a substance absorbs for a given temperature rise. This property is known as a substance's specific heat capacity.
Different molecules absorb different amounts of heat energy for each incremental increase in temperature; that is, they have different specific heat capacities. High specific heat capacity arises, in part, because certain substances' molecules possess more internal degrees of freedom than others do. For instance, room-temperature nitrogen
, which is a diatomic
molecule, has five active degrees of freedom: the three comprising translational motion plus two rotational degrees of freedom internally. Not surprisingly, in accordance with the equipartition theorem, nitrogen has five-thirds the specific heat capacity per mole
(a specific number of molecules) as do the monatomic gases. Another example is gasoline
(see table showing its specific heat capacity). Gasoline can absorb a large amount of heat energy per mole with only a modest temperature change because each molecule comprises an average of 21 atoms and therefore has many internal degrees of freedom. Even larger, more complex molecules can have dozens of internal degrees of freedom.
.gif)
Heat conduction
is the diffusion of heat energy from hot parts of a system to cold. A system can be either a single bulk entity or a plurality of discrete bulk entities. The term bulk in this context means a statistically significant quantity of particles (which can be a microscopic amount). Whenever heat energy diffuses within an isolated system, temperature differences within the system decrease (and entropy
increases).
One particular heat conduction mechanism occurs when translational motion, the particle motion underlying temperature, transfers momentum
from particle to particle in collisions. In gases, these translational motions are of the nature shown above in Fig. 1. As can be seen in that animation, not only does momentum (heat) diffuse throughout the volume of the gas through serial collisions, but entire molecules or atoms can move forward into new territory, bringing their kinetic energy with them. Consequently, temperature differences equalize throughout gases very quickly—especially for light atoms or molecules; convection
speeds this process even more.
Translational motion in solids however, takes the form of phonon
s (see Fig. 4 at right). Phonons are constrained, quantized wave packets traveling at the speed of sound for a given substance. The manner in which phonons interact within a solid determines a variety of its properties, including its thermal conductivity. In electrically insulating solids, phonon-based heat conduction is usually inefficient and such solids are considered thermal insulators (such as glass, plastic, rubber, ceramic, and rock). This is because in solids, atoms and molecules are locked into place relative to their neighbors and are not free to roam.
Metal
s however, are not restricted to only phonon-based heat conduction. Heat energy conducts through metals extraordinarily quickly because instead of direct molecule-to-molecule collisions, the vast majority of heat energy is mediated via very light, mobile conduction electron
s. This is why there is a near-perfect correlation between metals' thermal conductivity
and their electrical conductivity. Conduction electrons imbue metals with their extraordinary conductivity because they are delocalized
(i.e., not tied to a specific atom) and behave rather like a sort of quantum gas due to the effects of zero-point energy
(for more on ZPE, see Note 1 below). Furthermore, electrons are relatively light with a rest mass only th that of a proton
. This is about the same ratio as a .22 Short
bullet (29 grains
or 1.88 g
) compared to the rifle that shoots it. As Isaac Newton
wrote with his third law of motion,
However, a bullet accelerates faster than a rifle given an equal force. Since kinetic energy increases as the square of velocity, nearly all the kinetic energy goes into the bullet, not the rifle, even though both experience the same force from the expanding propellant gases. In the same manner, because they are much less massive, heat energy is readily borne by mobile conduction electrons. Additionally, because they're delocalized and very fast, kinetic heat energy conducts extremely quickly through metals with abundant conduction electrons.
Thermal radiation
is a byproduct of the collisions arising from atoms' various vibrational motions. These collisions cause the atoms' electrons to emit thermal photon
s (known as black-body radiation). Photons are emitted anytime an electric charge is accelerated (as happens when two atoms' electron clouds collide). Even individual molecules with internal temperatures greater than absolute zero also emit black-body radiation from their atoms. In any bulk quantity of a substance at equilibrium, black-body photons are emitted across a range of wavelength
s in a spectrum that has a bell curve-like shape called a Planck curve
(see graph in Fig. 5 at right). The top of a Planck curve (the peak emittance wavelength
) is located in a particular part of the electromagnetic spectrum
depending on the temperature of the black-body. Substances at extreme cryogenic
temperatures emit at long radio wavelengths whereas extremely hot temperatures produce short gamma ray
s (see Table of common temperatures).
Black-body radiation diffuses heat energy throughout a substance as the photons are absorbed by neighboring atoms, transferring momentum in the process. Black-body photons also easily escape from a substance and can be absorbed by the ambient environment; kinetic energy is lost in the process.
As established by the Stefan–Boltzmann law, the intensity of black-body radiation increases as the fourth power of absolute temperature. Thus, a black-body at 824 K (just short of glowing dull red) emits 60 times the radiant power
as it does at 296 K (room temperature). This is why one can so easily feel the radiant heat from hot objects at a distance. At higher temperatures, such as those found in an incandescent lamp
, black-body radiation can be the principal mechanism by which heat energy escapes a system.
, and some notable points between them are shown in the table below.
A The 2500 K value is approximate.
B For a true blackbody (which tungsten filaments are not). Tungsten filaments’ emissivity is greater at shorter wavelengths, which makes them appear whiter.
C Effective photosphere temperature.
D For a true blackbody (which the plasma was not). The Z machine’s dominant emission originated from 40 MK electrons (soft x–ray emissions) within the plasma.
The kinetic energy of particle motion is just one contributor to the total heat energy in a substance; another is phase transition
s, which are the potential energy
of molecular bonds that can form in a substance as it cools (such as during condensing
and freezing
). The heat energy required for a phase transition is called latent heat
. This phenomenon may more easily be grasped by considering it in the reverse direction: latent heat is the energy required to break chemical bonds (such as during evaporation
and melting
). Most everyone is familiar with the effects of phase transitions; for instance, steam
at 100 °C can cause severe burns much faster than the 100 °C air from a hair dryer
. This occurs because a large amount of latent heat is liberated as steam condenses into liquid water on the skin.
Even though heat energy is liberated or absorbed during phase transitions, pure chemical element
s, compounds
, and eutectic
alloy
s exhibit no temperature change whatsoever while they undergo them (see Fig. 7, below right). Consider one particular type of phase transition: melting. When a solid is melting, crystal lattice
chemical bond
s are being broken apart; the substance is transitioning from what is known as a more ordered state to a less ordered state. In Fig. 7, the melting of ice is shown within the lower left box heading from blue to green.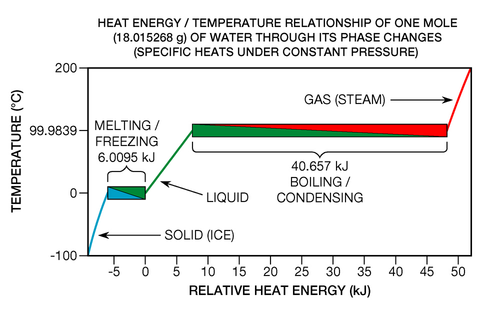
At one specific thermodynamic point, the melting point
(which is 0 °C across a wide pressure range in the case of water), all the atoms or molecules are, on average, at the maximum energy threshold their chemical bonds can withstand without breaking away from the lattice. Chemical bonds are quantized
forces: they either hold fast, or break; there is no in-between state. Consequently, when a substance is at its melting point, every joule
of added heat energy only breaks the bonds of a specific quantity of its atoms or molecules, converting them into a liquid of precisely the same temperature; no kinetic energy is added to translational motion (which is what gives substances their temperature). The effect is rather like popcorn
: at a certain temperature, additional heat energy can't make the kernels any hotter until the transition (popping) is complete. If the process is reversed (as in the freezing of a liquid), heat energy must be removed from a substance.
As stated above, the heat energy required for a phase transition is called latent heat. In the specific cases of melting and freezing, it's called enthalpy of fusion or heat of fusion. If the molecular bonds in a crystal lattice are strong, the heat of fusion can be relatively great, typically in the range of 6 to 30 kJ per mole for water and most of the metallic elements. If the substance is one of the monatomic gases, (which have little tendency to form molecular bonds) the heat of fusion is more modest, ranging from 0.021 to 2.3 kJ per mole. Relatively speaking, phase transitions can be truly energetic events. To completely melt ice at 0 °C into water at 0 °C, one must add roughly 80 times the heat energy as is required to increase the temperature of the same mass of liquid water by one degree Celsius. The metals' ratios are even greater, typically in the range of 400 to 1200 times. And the phase transition of boiling
is much more energetic than freezing. For instance, the energy required to completely boil or vaporize water (what is known as enthalpy of vaporization
) is roughly 540 times that required for a one-degree increase.
Water's sizable enthalpy of vaporization is why one's skin can be burned so quickly as steam condenses on it (heading from red to green in Fig. 7 above). In the opposite direction, this is why one's skin feels cool as liquid water on it evaporates (a process that occurs at a sub-ambient wet-bulb temperature
that is dependent on relative humidity
). Water's highly energetic enthalpy of vaporization is also an important factor underlying why solar pool covers (floating, insulated blankets that cover swimming pool
s when not in use) are so effective at reducing heating costs: they prevent evaporation. For instance, the evaporation of just 20 mm of water from a 1.29-meter-deep pool chills its water 8.4 degrees Celsius (15.1 °F).
of a substance, which is its total heat energy. The term internal energy mustn't be confused with internal degrees of freedom. Whereas the internal degrees of freedom of molecules refers to one particular place where kinetic energy is bound, the internal energy of a substance comprises all forms of heat energy.
Note that whereas absolute zero is the point of zero thermodynamic temperature and is also the point at which the particle constituents of matter have minimal motion, absolute zero is not necessarily the point at which a substance contains zero heat energy; one must be very precise with what one means by heat energy. Often, all the phase changes that can occur in a substance, will have occurred by the time it reaches absolute zero. However, this is not always the case. Notably, T=0 helium
remains liquid at room pressure and must be under a pressure of at least 25 bar (2.5 MPa) to crystallize. This is because helium's heat of fusion (the energy required to melt helium ice) is so low (only 21 joules per mole) that the motion-inducing effect of zero-point energy is sufficient to prevent it from freezing at lower pressures. Only if under at least 25 bar (2.5 MPa) of pressure will this latent heat energy be liberated as helium freezes while approaching absolute zero. A further complication is that many solids change their crystal structure to more compact arrangements at extremely high pressures (up to millions of bars, or hundreds of gigapascals). These are known as solid-solid phase transitions wherein latent heat is liberated as a crystal lattice changes to a more thermodynamically favorable, compact one.
The above complexities make for rather cumbersome blanket statements regarding the internal energy in T=0 substances. Regardless of pressure though, what can be said is that at absolute zero, all solids with a lowest-energy crystal lattice such those with a closest-packed arrangement
(see Fig. 8, above left) contain minimal internal energy, retaining only that due to the ever-present background of zero-point energy. One can also say that for a given substance at constant pressure, absolute zero is the point of lowest enthalpy
(a measure of work potential that takes internal energy, pressure, and volume into consideration). Lastly, it is always true to say that all T=0 substances contain zero kinetic heat energy.
of temperature/pressure proportionality, solutions to everyday problems are straightforward; for instance, calculating how a temperature change affects the pressure inside an automobile tire. If the tire has a relatively cold pressure of 200 kPa
-gage, then in absolute terms (relative to a vacuum), its pressure is 300 kPa-absolute. Room temperature ("cold" in tire terms) is 296 K. If the tire pressure is 20 °C hotter (20 kelvins), the solution is calculated as = 6.8% greater thermodynamic temperature and absolute pressure; that is, a pressure of 320 kPa-absolute, which is 220 kPa-gage.
Earth's
proximity to the Sun
is why almost everything near Earth's surface is warm with a temperature substantially above absolute zero. Solar radiation constantly replenishes heat energy that Earth loses into space and a relatively stable state of near equilibrium is achieved. Because of the wide variety of heat diffusion mechanisms (one of which is black-body radiation which occurs at the speed of light), objects on Earth rarely vary too far from the global mean surface and air temperature of 287 to 288 K (14 to 15 °C). The more an object's or system's temperature varies from this average, the more rapidly it tends to come back into equilibrium with the ambient environment.
s, molecule
s, electron
s, photon
s) are at equilibrium
, so that their energies obey a Boltzmann distribution
(or its quantum mechanical
counterpart). There are many possible scales of temperature, derived from a variety of observations of physical phenomena. The thermodynamic temperature can be shown to have special properties, and in particular can be seen to be uniquely defined (up to some constant multiplicative factor) by considering the efficiency
of idealized heat engine
s. Thus the ratio
T2/T1 of two temperaturesT1 andT2 is the same in all absolute scales.
Loosely stated, temperature controls the flow of heat between two systems, and the universe
as a whole, as with any natural system, tends to progress so as to maximize entropy
. This suggests that there should be a relationship between temperature and entropy. To elucidate this, consider first the relationship between heat, work
and temperature. One way to study this is to analyze a heat engine, which is a device for converting heat into mechanical work, such as the Carnot heat engine
. Such a heat engine functions by using a temperature gradient between a high temperatureTH and a low temperature TC to generate work, and the work done (per cycle, say) by the heat engine is equal to the difference between the heat energy qH put into the system at the high temperature and the heat qC ejected at the low temperature (in that cycle). The efficiency of the engine is the work divided by the heat put into the system or
where wcy is the work done per cycle. Thus the efficiency depends only on qC/qH.
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient.
Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to say, the effiency is the function of only temperatures
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. A quick way to see this is that should this not be the case, then energy (in the form of Q) will be wasted or gained, resulting in different overall efficiencies every time a cycle is split into component cycles; clearly a cycle can be composed of any number of smaller cycles.
With this understanding of Q1, Q2 and Q3, we note also that mathematically,
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and is one of the principal parameters of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
. Thermodynamic temperature is an "absolute" scale
Scale of temperature
Scale of temperature is a way to measure temperature quantitatively.-Formal description:According to the zeroth law of thermodynamics, being in thermal equilibrium is an equivalence relation. Thus all thermal systems may be divided into a quotient set by this equivalence relation, denoted below as M...
because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
, is the temperature at which the particle constituents of matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
have minimal motion and can become no colder.
At its simplest, temperature arises from the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the vibrational motions of matter's
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
particle constituents (molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s, atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, and subatomic particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s). The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, contribute the total thermal energy
Thermal energy
Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....
(loosely, the heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
energy) within a substance. Thus, thermal energy may be stored in a number of ways within a substance, but only the kinetic energy of particles contributes to the substance's temperature.
Overview
Temperature arises from the random submicroscopic vibrations of the particle constituents of matterMatter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
. These motions comprise the kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
in a substance. More specifically, the thermodynamic temperature of any bulk quantity of matter is the measure of the average kinetic energy of a certain kind of vibrational motion of its constituent particles called translational motions. Translational motions are ordinary, whole-body movements in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
whereby particles move about and exchange energy in collisions. Figure 1 below shows translational motion in gases; Figure 4 below shows translational motion in solids. Thermodynamic temperature's null
Null (mathematics)
In mathematics, the word null means of or related to having zero members in a set or a value of zero...
point, absolute zero, is the temperature at which the particle constituents of matter are as close as possible to complete rest; that is, they have minimal motion, retaining only quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
motion. Zero kinetic energy remains in a substance at absolute zero (see Heat energy at absolute zero, below).
Throughout the scientific world where measurements are made in SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
units, thermodynamic temperature is measured in kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s (symbol: K). Many engineering fields in the U.S.
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
however, measure thermodynamic temperature using the Rankine scale.
By international agreement, the unit kelvin and its scale are defined by two points: absolute zero, and the triple point
Triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
of Vienna Standard Mean Ocean Water (water with a specified blend of hydrogen and oxygen isotopes). Absolute zero, the lowest possible temperature, is defined as being precisely 0 K and −273.15 °C
Celsius
Celsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
. The triple point
Triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
of water is defined as being precisely 273.16 K and 0.01 °C. This definition does three things:
- It fixes the magnitude of the kelvin unit as being precisely 1 part in 273.16 parts the difference between absolute zero and the triple point of water;
- It establishes that one kelvin has precisely the same magnitude as a one-degree increment on the CelsiusCelsiusCelsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
scale; and - It establishes the difference between the two scales' null points as being precisely 273.15 kelvins (0 K = −273.15 °C and 273.16 K = 0.01 °C).
Temperatures expressed in kelvins are converted to degrees Rankine simply by multiplying by 1.8 as follows: T°R = 1.8TK, where TK and T°R are temperatures in kelvin and degrees Rankine respectively. Temperatures expressed in degrees Rankine are converted to kelvins by dividing by 1.8 as follows: TK = .
Practical realization
Although the Kelvin and Celsius scales are defined using absolute zero (0 K) and the triple point of water (273.16 K and 0.01 °C), it is impractical to use this definition at temperatures that are very different from the triple point of water. ITS-90 is then designed to represent the thermodynamic temperature as closely as possible throughout its range. Many different thermometer designs are required to cover the entire range. These include helium vapor pressure thermometers, helium gas thermometers, standard platinum resistance thermometersResistance thermometer
Resistance thermometers, also called resistance temperature detectors or resistive thermal devices , are sensors used to measure temperature by correlating the resistance of the RTD element with temperature. Most RTD elements consist of a length of fine coiled wire wrapped around a ceramic or glass...
(known as SPRTs, PRTs or Platium RTDs) and monochromatic radiation thermometers
Infrared thermometer
Infrared thermometers infer temperature using a portion of the thermal radiation sometimes called blackbody radiation emitted by the object of measurement. They are sometimes called laser thermometers if a laser is used to help aim the thermometer, or non-contact thermometers to describe the...
.
The relationship of temperature, motions, conduction, and heat energy
The nature of kinetic energy, translational motion, and temperature
At its simplest, temperature arises from the kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the vibrational motions of matter's
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
particle constituents (molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s, atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, and subatomic particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s). The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, contribute the total thermal energy
Thermal energy
Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....
(loosely, the heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
energy) within a substance. Thus, thermal energy may be stored in a number of ways within a substance, but only the kinetic energy of particles contributes to the substance's temperature. The heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
, which relates heat input and temperature change, is discussed below.
The relationship of kinetic energy, mass, and velocity is given by the formula Ek = mv2. Accordingly, particles with one unit of mass moving at one unit of velocity have precisely the same kinetic energy, and precisely the same temperature, as those with four times the mass but half the velocity.
The thermodynamic temperature of any bulk quantity of a substance (a statistically significant quantity of particles) is directly proportional to the mean average kinetic energy of a specific kind of particle motion known as translational motion. These simple movements in the three x, y, and z–axis dimensions of space means the particles move in the three spatial degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
. This particular form of kinetic energy is sometimes referred to as kinetic temperature. Translational motion is but one form of heat energy and is what gives gases not only their temperature, but also their pressure and the vast majority of their volume. This relationship between the temperature, pressure, and volume of gases is established by the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
's formula pV = nRT and is embodied in the gas laws
Gas laws
The early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
.
The extent to which the kinetic energy of translational motion of an individual atom or molecule (particle) in a gas contributes to the pressure and volume of that gas is a proportional function of thermodynamic temperature as established by the Boltzmann constant (symbol: kB). The Boltzmann constant also relates the thermodynamic temperature of a gas to the mean kinetic energy of an individual particle's translational motion as follows:
where:
-
is the mean kinetic energy in jouleJouleThe joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s (J) and is pronounced “E bar” - kB = and is pronounced “Kay sub bee”
- T is the thermodynamic temperature in kelvins (K)
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
(all parts are at a uniform temperature and no heat is going into or out of it), the translational motions of individual atoms and molecules occurs across a wide range of speeds (see animation in Figure 1 above). At any one instant, the proportion of particles moving at a given speed within this range is determined by probability as described by the Maxwell–Boltzmann distribution. The graph shown here in Fig. 2 shows the speed distribution of 5500 K helium atoms. They have a most probable speed of 4.780 km/s. However, a certain proportion of atoms at any given instant are moving faster while others are moving relatively slowly; some are momentarily at a virtual standstill (off the x–axis to the right). This graph uses inverse speed for its x–axis so the shape of the curve can easily be compared to the curves in Figure 5 below. In both graphs, zero on the x–axis represents infinite temperature. Additionally, the x and y–axis on both graphs are scaled proportionally.
The high speeds of translational motion
Although very specialized laboratory equipment is required to directly detect translational motions, the resultant collisions by atoms or molecules with small particles suspended in a fluidFluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
produces Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
that can be seen with an ordinary microscope. The translational motions of elementary particles are very fast and temperatures close to absolute zero are required to directly observe them. For instance, when scientists at the NIST
National Institute of Standards and Technology
The National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
achieved a record-setting cold temperature of 700 nK (billionths of a kelvin) in 1994, they used optical lattice
Optical lattice
An optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate in the locations of potential minima...
laser equipment to adiabatically
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
cool caesium
Caesium
Caesium or cesium is the chemical element with the symbol Cs and atomic number 55. It is a soft, silvery-gold alkali metal with a melting point of 28 °C , which makes it one of only five elemental metals that are liquid at room temperature...
atoms. They then turned off the entrapment lasers and directly measured atom velocities of 7 mm per second in order to calculate their temperature. Formulas for calculating the velocity and speed of translational motion are given in the following footnote.
The internal motions of molecules and specific heat
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s are complex objects; they are a population of atoms and thermal agitation can strain their internal chemical bond
Chemical bond
A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
s in three different ways: via rotation, bond length, and bond angle movements. These are all types of internal degrees of freedom. This makes molecules distinct from monatomic substances (consisting of individual atoms) like the noble gas
Noble gas
The noble gases are a group of chemical elements with very similar properties: under standard conditions, they are all odorless, colorless, monatomic gases, with very low chemical reactivity...
es helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
and argon
Argon
Argon is a chemical element represented by the symbol Ar. Argon has atomic number 18 and is the third element in group 18 of the periodic table . Argon is the third most common gas in the Earth's atmosphere, at 0.93%, making it more common than carbon dioxide...
, which have only the three translational degrees of freedom. Kinetic energy is stored in molecules' internal degrees of freedom, which gives them an internal temperature. Even though these motions are called internal, the external portions of molecules still move—rather like the jiggling of a stationary water balloon
Water balloon
A water balloon or water bomb is a latex rubber balloon filled with water. They are commonly used in water balloon fights and as a practical joke device.-History:...
. This permits the two-way exchange of kinetic energy between internal motions and translational motions with each molecular collision. Accordingly, as heat is removed from molecules, both their kinetic temperature (the kinetic energy of translational motion) and their internal temperature simultaneously diminish in equal proportions. This phenomenon is described by the equipartition theorem
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
, which states that for any bulk quantity of a substance in equilibrium, the kinetic energy of particle motion is evenly distributed among all the active degrees of freedom available to the particles. Since the internal temperature of molecules are usually equal to their kinetic temperature, the distinction is usually of interest only in the detailed study of non-local thermodynamic equilibrium (LTE) phenomena such as combustion
Combustion
Combustion or burning is the sequence of exothermic chemical reactions between a fuel and an oxidant accompanied by the production of heat and conversion of chemical species. The release of heat can result in the production of light in the form of either glowing or a flame...
, the sublimation of solids, and the diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
of hot gases in a partial vacuum.
The kinetic energy stored internally in molecules causes substances to contain more heat energy at any given temperature and to absorb additional heat energy for a given temperature increase. This is because any kinetic energy that is, at a given instant, bound in internal motions is not at that same instant contributing to the molecules' translational motions. This extra kinetic energy simply increases the amount of heat energy a substance absorbs for a given temperature rise. This property is known as a substance's specific heat capacity.
Different molecules absorb different amounts of heat energy for each incremental increase in temperature; that is, they have different specific heat capacities. High specific heat capacity arises, in part, because certain substances' molecules possess more internal degrees of freedom than others do. For instance, room-temperature nitrogen
Nitrogen
Nitrogen is a chemical element that has the symbol N, atomic number of 7 and atomic mass 14.00674 u. Elemental nitrogen is a colorless, odorless, tasteless, and mostly inert diatomic gas at standard conditions, constituting 78.08% by volume of Earth's atmosphere...
, which is a diatomic
Diatomic
Diatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...
molecule, has five active degrees of freedom: the three comprising translational motion plus two rotational degrees of freedom internally. Not surprisingly, in accordance with the equipartition theorem, nitrogen has five-thirds the specific heat capacity per mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
(a specific number of molecules) as do the monatomic gases. Another example is gasoline
Gasoline
Gasoline , or petrol , is a toxic, translucent, petroleum-derived liquid that is primarily used as a fuel in internal combustion engines. It consists mostly of organic compounds obtained by the fractional distillation of petroleum, enhanced with a variety of additives. Some gasolines also contain...
(see table showing its specific heat capacity). Gasoline can absorb a large amount of heat energy per mole with only a modest temperature change because each molecule comprises an average of 21 atoms and therefore has many internal degrees of freedom. Even larger, more complex molecules can have dozens of internal degrees of freedom.
The diffusion of heat energy: Entropy, phonons, and mobile conduction electrons
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
is the diffusion of heat energy from hot parts of a system to cold. A system can be either a single bulk entity or a plurality of discrete bulk entities. The term bulk in this context means a statistically significant quantity of particles (which can be a microscopic amount). Whenever heat energy diffuses within an isolated system, temperature differences within the system decrease (and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
increases).
One particular heat conduction mechanism occurs when translational motion, the particle motion underlying temperature, transfers momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
from particle to particle in collisions. In gases, these translational motions are of the nature shown above in Fig. 1. As can be seen in that animation, not only does momentum (heat) diffuse throughout the volume of the gas through serial collisions, but entire molecules or atoms can move forward into new territory, bringing their kinetic energy with them. Consequently, temperature differences equalize throughout gases very quickly—especially for light atoms or molecules; convection
Convective heat transfer
Convective heat transfer, often referred to as convection, is the transfer of heat from one place to another by the movement of fluids. The presence of bulk motion of the fluid enhances the heat transfer between the solid surface and the fluid. Convection is usually the dominant form of heat...
speeds this process even more.
Translational motion in solids however, takes the form of phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s (see Fig. 4 at right). Phonons are constrained, quantized wave packets traveling at the speed of sound for a given substance. The manner in which phonons interact within a solid determines a variety of its properties, including its thermal conductivity. In electrically insulating solids, phonon-based heat conduction is usually inefficient and such solids are considered thermal insulators (such as glass, plastic, rubber, ceramic, and rock). This is because in solids, atoms and molecules are locked into place relative to their neighbors and are not free to roam.
Metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s however, are not restricted to only phonon-based heat conduction. Heat energy conducts through metals extraordinarily quickly because instead of direct molecule-to-molecule collisions, the vast majority of heat energy is mediated via very light, mobile conduction electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s. This is why there is a near-perfect correlation between metals' thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
and their electrical conductivity. Conduction electrons imbue metals with their extraordinary conductivity because they are delocalized
Delocalized electron
In chemistry, delocalized electrons are electrons in a molecule, ion or solid metal that are not associated with a single atom or one covalent bond....
(i.e., not tied to a specific atom) and behave rather like a sort of quantum gas due to the effects of zero-point energy
Zero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
(for more on ZPE, see Note 1 below). Furthermore, electrons are relatively light with a rest mass only th that of a proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
. This is about the same ratio as a .22 Short
.22 Short
.22 Short is a variety of .22 caliber rimfire ammunition. Developed in 1857 for the first Smith and Wesson revolver, the .22 rimfire was the first American metallic cartridge....
bullet (29 grains
Grain (measure)
A grain is a unit of measurement of mass that is nominally based upon the mass of a single seed of a cereal. From the Bronze Age into the Renaissance the average masses of wheat and barley grains were part of the legal definition of units of mass. However, there is no evidence of any country ever...
or 1.88 g
Gram
The gram is a metric system unit of mass....
) compared to the rifle that shoots it. As Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
wrote with his third law of motion,
However, a bullet accelerates faster than a rifle given an equal force. Since kinetic energy increases as the square of velocity, nearly all the kinetic energy goes into the bullet, not the rifle, even though both experience the same force from the expanding propellant gases. In the same manner, because they are much less massive, heat energy is readily borne by mobile conduction electrons. Additionally, because they're delocalized and very fast, kinetic heat energy conducts extremely quickly through metals with abundant conduction electrons.
The diffusion of heat energy: Black-body radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
is a byproduct of the collisions arising from atoms' various vibrational motions. These collisions cause the atoms' electrons to emit thermal photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s (known as black-body radiation). Photons are emitted anytime an electric charge is accelerated (as happens when two atoms' electron clouds collide). Even individual molecules with internal temperatures greater than absolute zero also emit black-body radiation from their atoms. In any bulk quantity of a substance at equilibrium, black-body photons are emitted across a range of wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s in a spectrum that has a bell curve-like shape called a Planck curve
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
(see graph in Fig. 5 at right). The top of a Planck curve (the peak emittance wavelength
Wien's displacement law
Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
) is located in a particular part of the electromagnetic spectrum
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
depending on the temperature of the black-body. Substances at extreme cryogenic
Cryogenics
In physics, cryogenics is the study of the production of very low temperature and the behavior of materials at those temperatures. A person who studies elements under extremely cold temperature is called a cryogenicist. Rather than the relative temperature scales of Celsius and Fahrenheit,...
temperatures emit at long radio wavelengths whereas extremely hot temperatures produce short gamma ray
Gamma ray
Gamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei...
s (see Table of common temperatures).
Black-body radiation diffuses heat energy throughout a substance as the photons are absorbed by neighboring atoms, transferring momentum in the process. Black-body photons also easily escape from a substance and can be absorbed by the ambient environment; kinetic energy is lost in the process.
As established by the Stefan–Boltzmann law, the intensity of black-body radiation increases as the fourth power of absolute temperature. Thus, a black-body at 824 K (just short of glowing dull red) emits 60 times the radiant power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
as it does at 296 K (room temperature). This is why one can so easily feel the radiant heat from hot objects at a distance. At higher temperatures, such as those found in an incandescent lamp
Incandescent light bulb
The incandescent light bulb, incandescent lamp or incandescent light globe makes light by heating a metal filament wire to a high temperature until it glows. The hot filament is protected from air by a glass bulb that is filled with inert gas or evacuated. In a halogen lamp, a chemical process...
, black-body radiation can be the principal mechanism by which heat energy escapes a system.
Table of thermodynamic temperatures
The full range of the thermodynamic temperature scale, from absolute zero to absolute hotAbsolute hot
Absolute hot is a concept of temperature that postulates the existence of a highest attainable temperature of matter. The idea has been popularized by the television series Nova...
, and some notable points between them are shown in the table below.
| kelvin | Peak emittance wavelength Wavelength In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a... of black-body photons Wien's displacement law Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph... |
|
| Absolute zero Absolute zero Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means.... (precisely by definition) |
0 K | ∞ Infinity Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity... |
| Coldest measured temperature |
450 pK | 6,400 kilometers Kilometre The kilometre is a unit of length in the metric system, equal to one thousand metres and is therefore exactly equal to the distance travelled by light in free space in of a second... |
| One millikelvin (precisely by definition) |
0.001 K | 2.897 77 meters Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... (Radio, FM band FM broadcasting FM broadcasting is a broadcasting technology pioneered by Edwin Howard Armstrong which uses frequency modulation to provide high-fidelity sound over broadcast radio. The term "FM band" describes the "frequency band in which FM is used for broadcasting"... ) |
| Water's triple point Triple point In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium... (precisely by definition) |
273.16 K | 10,608.3 nm (Long wavelength I.R. Infrared Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm... ) |
| Incandescent lamp Incandescent light bulb The incandescent light bulb, incandescent lamp or incandescent light globe makes light by heating a metal filament wire to a high temperature until it glows. The hot filament is protected from air by a glass bulb that is filled with inert gas or evacuated. In a halogen lamp, a chemical process... B |
2500 K | 1160 nm (Near infrared Infrared Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm... )C |
| Sun’s Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... visible surfaceC |
5778 K | 501.5 nm (Green light) |
| Lightning bolt’s Lightning Lightning is an atmospheric electrostatic discharge accompanied by thunder, which typically occurs during thunderstorms, and sometimes during volcanic eruptions or dust storms... channel |
28,000 K | 100 nm (Far Ultraviolet Ultraviolet Ultraviolet light is electromagnetic radiation with a wavelength shorter than that of visible light, but longer than X-rays, in the range 10 nm to 400 nm, and energies from 3 eV to 124 eV... light) |
| Sun’s core | 16 MK | 0.18 nm (X-ray X-ray X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma... s) |
| Thermonuclear weapon Nuclear weapon A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions, either fission or a combination of fission and fusion. Both reactions release vast quantities of energy from relatively small amounts of matter. The first fission bomb test released the same amount... (peak temperature) |
350 MK | 8.3 × 10−3 nm (Gamma ray Gamma ray Gamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei... s) |
| Sandia National Labs’ Z machine Z machine The Z machine is the largest X-ray generator in the world and is designed to test materials in conditions of extreme temperature and pressure. Operated by Sandia National Laboratories, it gathers data to aid in computer modeling of nuclear weapons... D |
2 GK | 1.4 × 10−3 nm (Gamma rays) |
| Core of a high–mass star on its last day Silicon burning process In astrophysics, silicon burning is a very brief sequence of nuclear fusion reactions that occur in massive stars with a minimum of about 8–11 solar masses. Silicon burning is the final stage of fusion for massive stars that have run out of the fuels that power them for their long lives in the main... |
3 GK | 1 × 10−3 nm (Gamma rays) |
| Merging binary neutron star Neutron star A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger... system |
350 GK | 8 × 10−6 nm (Gamma rays) |
| Gamma-ray burst progenitors |
1 TK | 3 × 10−6 nm (Gamma rays) |
| Relativistic Heavy Ion Collider Relativistic Heavy Ion Collider The Relativistic Heavy Ion Collider is one of two existing heavy-ion colliders, and the only spin-polarized proton collider in the world. It is located at Brookhaven National Laboratory in Upton, New York and operated by an international team of researchers... |
1 TK | 3 × 10−6 nm (Gamma rays) |
| CERN’s CERN The European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border... proton vs. nucleus collisions |
10 TK | 3 × 10−7 nm (Gamma rays) |
| Universe 5.391 × 10−44 s Planck time In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length... after the Big Bang Big Bang The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in... |
1.417 × 1032 K Planck temperature Planck temperature is the greatest physically-possible temperature, according the set of theories proposed by the German physicist Max Planck. It's part of a system of five natural units known as Planck units, based on universal physical constants.... |
1.616 × 10−26 nm (Planck frequency) |
A The 2500 K value is approximate.
B For a true blackbody (which tungsten filaments are not). Tungsten filaments’ emissivity is greater at shorter wavelengths, which makes them appear whiter.
C Effective photosphere temperature.
D For a true blackbody (which the plasma was not). The Z machine’s dominant emission originated from 40 MK electrons (soft x–ray emissions) within the plasma.
The heat of phase changes
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s, which are the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of molecular bonds that can form in a substance as it cools (such as during condensing
Condensation
Condensation is the change of the physical state of matter from gaseous phase into liquid phase, and is the reverse of vaporization. When the transition happens from the gaseous phase into the solid phase directly, the change is called deposition....
and freezing
Freezing
Freezing or solidification is a phase change in which a liquid turns into a solid when its temperature is lowered below its freezing point. The reverse process is melting....
). The heat energy required for a phase transition is called latent heat
Latent heat
Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was...
. This phenomenon may more easily be grasped by considering it in the reverse direction: latent heat is the energy required to break chemical bonds (such as during evaporation
Evaporation
Evaporation is a type of vaporization of a liquid that occurs only on the surface of a liquid. The other type of vaporization is boiling, which, instead, occurs on the entire mass of the liquid....
and melting
Melting
Melting, or fusion, is a physical process that results in the phase change of a substance from a solid to a liquid. The internal energy of a substance is increased, typically by the application of heat or pressure, resulting in a rise of its temperature to the melting point, at which the rigid...
). Most everyone is familiar with the effects of phase transitions; for instance, steam
Steam
Steam is the technical term for water vapor, the gaseous phase of water, which is formed when water boils. In common language it is often used to refer to the visible mist of water droplets formed as this water vapor condenses in the presence of cooler air...
at 100 °C can cause severe burns much faster than the 100 °C air from a hair dryer
Blowdryer
A blowdryer or hairdryer is an electromechanical device designed to blow cool or hot air over wet or damp hair, in order to accelerate the evaporation of water particles and dry the hair. Blowdryers allow to better control the shape and style of hair, by accelerating and controlling the formation...
. This occurs because a large amount of latent heat is liberated as steam condenses into liquid water on the skin.
Even though heat energy is liberated or absorbed during phase transitions, pure chemical element
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
s, compounds
Chemical compound
A chemical compound is a pure chemical substance consisting of two or more different chemical elements that can be separated into simpler substances by chemical reactions. Chemical compounds have a unique and defined chemical structure; they consist of a fixed ratio of atoms that are held together...
, and eutectic
Eutectic point
A eutectic system is a mixture of chemical compounds or elements that has a single chemical composition that solidifies at a lower temperature than any other composition. This composition is known as the eutectic composition and the temperature is known as the eutectic temperature...
alloy
Alloy
An alloy is a mixture or metallic solid solution composed of two or more elements. Complete solid solution alloys give single solid phase microstructure, while partial solutions give two or more phases that may or may not be homogeneous in distribution, depending on thermal history...
s exhibit no temperature change whatsoever while they undergo them (see Fig. 7, below right). Consider one particular type of phase transition: melting. When a solid is melting, crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
chemical bond
Chemical bond
A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
s are being broken apart; the substance is transitioning from what is known as a more ordered state to a less ordered state. In Fig. 7, the melting of ice is shown within the lower left box heading from blue to green.
Melting point
The melting point of a solid is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at standard atmospheric pressure...
(which is 0 °C across a wide pressure range in the case of water), all the atoms or molecules are, on average, at the maximum energy threshold their chemical bonds can withstand without breaking away from the lattice. Chemical bonds are quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
forces: they either hold fast, or break; there is no in-between state. Consequently, when a substance is at its melting point, every joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
of added heat energy only breaks the bonds of a specific quantity of its atoms or molecules, converting them into a liquid of precisely the same temperature; no kinetic energy is added to translational motion (which is what gives substances their temperature). The effect is rather like popcorn
Popcorn
Popcorn, or popping corn, is corn which expands from the kernel and puffs up when heated. Corn is able to pop because, like sorghum, quinoa and millet, its kernels have a hard moisture-sealed hull and a dense starchy interior. This allows pressure to build inside the kernel until an explosive...
: at a certain temperature, additional heat energy can't make the kernels any hotter until the transition (popping) is complete. If the process is reversed (as in the freezing of a liquid), heat energy must be removed from a substance.
As stated above, the heat energy required for a phase transition is called latent heat. In the specific cases of melting and freezing, it's called enthalpy of fusion or heat of fusion. If the molecular bonds in a crystal lattice are strong, the heat of fusion can be relatively great, typically in the range of 6 to 30 kJ per mole for water and most of the metallic elements. If the substance is one of the monatomic gases, (which have little tendency to form molecular bonds) the heat of fusion is more modest, ranging from 0.021 to 2.3 kJ per mole. Relatively speaking, phase transitions can be truly energetic events. To completely melt ice at 0 °C into water at 0 °C, one must add roughly 80 times the heat energy as is required to increase the temperature of the same mass of liquid water by one degree Celsius. The metals' ratios are even greater, typically in the range of 400 to 1200 times. And the phase transition of boiling
Boiling
Boiling is the rapid vaporization of a liquid, which occurs when a liquid is heated to its boiling point, the temperature at which the vapor pressure of the liquid is equal to the pressure exerted on the liquid by the surrounding environmental pressure. While below the boiling point a liquid...
is much more energetic than freezing. For instance, the energy required to completely boil or vaporize water (what is known as enthalpy of vaporization
Standard enthalpy change of vaporization
The enthalpy of vaporization, , also known as the heat of vaporization or heat of evaporation, is the energy required to transform a given quantity of a substance into a gas at a given pressure .It is often measured at the normal boiling point of a substance; although tabulated values are usually...
) is roughly 540 times that required for a one-degree increase.
Water's sizable enthalpy of vaporization is why one's skin can be burned so quickly as steam condenses on it (heading from red to green in Fig. 7 above). In the opposite direction, this is why one's skin feels cool as liquid water on it evaporates (a process that occurs at a sub-ambient wet-bulb temperature
Wet-bulb temperature
The wet-bulb temperature is a type of temperature measurement that reflects the physical properties of a system with a mixture of a gas and a vapor, usually air and water vapor. Wet bulb temperature is the lowest temperature that can be reached by the evaporation of water only. It is the...
that is dependent on relative humidity
Relative humidity
Relative humidity is a term used to describe the amount of water vapor in a mixture of air and water vapor. It is defined as the partial pressure of water vapor in the air-water mixture, given as a percentage of the saturated vapor pressure under those conditions...
). Water's highly energetic enthalpy of vaporization is also an important factor underlying why solar pool covers (floating, insulated blankets that cover swimming pool
Swimming pool
A swimming pool, swimming bath, wading pool, or simply a pool, is a container filled with water intended for swimming or water-based recreation. There are many standard sizes; the largest is the Olympic-size swimming pool...
s when not in use) are so effective at reducing heating costs: they prevent evaporation. For instance, the evaporation of just 20 mm of water from a 1.29-meter-deep pool chills its water 8.4 degrees Celsius (15.1 °F).
Internal energy
The total kinetic energy of all particle motion, including that of conduction electrons, plus the potential energy of phase changes, plus zero-point energy comprise the internal energyInternal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of a substance, which is its total heat energy. The term internal energy mustn't be confused with internal degrees of freedom. Whereas the internal degrees of freedom of molecules refers to one particular place where kinetic energy is bound, the internal energy of a substance comprises all forms of heat energy.
Heat energy at absolute zero
As a substance cools, different forms of heat energy and their related effects simultaneously decrease in magnitude: the latent heat of available phase transitions are liberated as a substance changes from a less ordered state to a more ordered state; the translational motions of atoms and molecules diminish (their kinetic temperature decreases); the internal motions of molecules diminish (their internal temperature decreases); conduction electrons (if the substance is an electrical conductor) travel somewhat slower; and black-body radiation's peak emittance wavelength increases (the photons' energy decreases). When the particles of a substance are as close as possible to complete rest and retain only ZPE-induced quantum mechanical motion, the substance is at the temperature of absolute zero (T=0).Note that whereas absolute zero is the point of zero thermodynamic temperature and is also the point at which the particle constituents of matter have minimal motion, absolute zero is not necessarily the point at which a substance contains zero heat energy; one must be very precise with what one means by heat energy. Often, all the phase changes that can occur in a substance, will have occurred by the time it reaches absolute zero. However, this is not always the case. Notably, T=0 helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
remains liquid at room pressure and must be under a pressure of at least 25 bar (2.5 MPa) to crystallize. This is because helium's heat of fusion (the energy required to melt helium ice) is so low (only 21 joules per mole) that the motion-inducing effect of zero-point energy is sufficient to prevent it from freezing at lower pressures. Only if under at least 25 bar (2.5 MPa) of pressure will this latent heat energy be liberated as helium freezes while approaching absolute zero. A further complication is that many solids change their crystal structure to more compact arrangements at extremely high pressures (up to millions of bars, or hundreds of gigapascals). These are known as solid-solid phase transitions wherein latent heat is liberated as a crystal lattice changes to a more thermodynamically favorable, compact one.
The above complexities make for rather cumbersome blanket statements regarding the internal energy in T=0 substances. Regardless of pressure though, what can be said is that at absolute zero, all solids with a lowest-energy crystal lattice such those with a closest-packed arrangement
Close-packing
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement . Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a regular lattice...
(see Fig. 8, above left) contain minimal internal energy, retaining only that due to the ever-present background of zero-point energy. One can also say that for a given substance at constant pressure, absolute zero is the point of lowest enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
(a measure of work potential that takes internal energy, pressure, and volume into consideration). Lastly, it is always true to say that all T=0 substances contain zero kinetic heat energy.
Practical applications for thermodynamic temperature
Thermodynamic temperature is useful not only for scientists, it can also be useful for lay-people in many disciplines involving gases. By expressing variables in absolute terms and applying Gay–Lussac's lawGay-Lussac's law
The expression Gay-Lussac's law is used for each of the two relationships named after the French chemist Joseph Louis Gay-Lussac and which concern the properties of gases, though it is more usually applied to his law of combining volumes, the first listed here...
of temperature/pressure proportionality, solutions to everyday problems are straightforward; for instance, calculating how a temperature change affects the pressure inside an automobile tire. If the tire has a relatively cold pressure of 200 kPa
Pascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
-gage, then in absolute terms (relative to a vacuum), its pressure is 300 kPa-absolute. Room temperature ("cold" in tire terms) is 296 K. If the tire pressure is 20 °C hotter (20 kelvins), the solution is calculated as = 6.8% greater thermodynamic temperature and absolute pressure; that is, a pressure of 320 kPa-absolute, which is 220 kPa-gage.
The origin of heat energy on Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
proximity to the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
is why almost everything near Earth's surface is warm with a temperature substantially above absolute zero. Solar radiation constantly replenishes heat energy that Earth loses into space and a relatively stable state of near equilibrium is achieved. Because of the wide variety of heat diffusion mechanisms (one of which is black-body radiation which occurs at the speed of light), objects on Earth rarely vary too far from the global mean surface and air temperature of 287 to 288 K (14 to 15 °C). The more an object's or system's temperature varies from this average, the more rapidly it tends to come back into equilibrium with the ambient environment.
Definition of thermodynamic temperature
Strictly speaking, the temperature of a system is well-defined only if its particles (atomAtom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s, electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s, photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s) are at equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, so that their energies obey a Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
(or its quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
counterpart). There are many possible scales of temperature, derived from a variety of observations of physical phenomena. The thermodynamic temperature can be shown to have special properties, and in particular can be seen to be uniquely defined (up to some constant multiplicative factor) by considering the efficiency
Energy conversion efficiency
Energy conversion efficiency is the ratio between the useful output of an energy conversion machine and the input, in energy terms. The useful output may be electric power, mechanical work, or heat.-Overview:...
of idealized heat engine
Heat engine
In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. It does this by bringing a working substance from a high temperature state to a lower temperature state. A heat "source" generates thermal energy that brings the working substance...
s. Thus the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
T2/T1 of two temperaturesT1 andT2 is the same in all absolute scales.
Loosely stated, temperature controls the flow of heat between two systems, and the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
as a whole, as with any natural system, tends to progress so as to maximize entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. This suggests that there should be a relationship between temperature and entropy. To elucidate this, consider first the relationship between heat, work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
and temperature. One way to study this is to analyze a heat engine, which is a device for converting heat into mechanical work, such as the Carnot heat engine
Carnot heat engine
A Carnot heat engine is a hypothetical engine that operates on the reversible Carnot cycle. The basic model for this engine was developed by Nicolas Léonard Sadi Carnot in 1824...
. Such a heat engine functions by using a temperature gradient between a high temperatureTH and a low temperature TC to generate work, and the work done (per cycle, say) by the heat engine is equal to the difference between the heat energy qH put into the system at the high temperature and the heat qC ejected at the low temperature (in that cycle). The efficiency of the engine is the work divided by the heat put into the system or
where wcy is the work done per cycle. Thus the efficiency depends only on qC/qH.
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient.
Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to say, the effiency is the function of only temperatures
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. A quick way to see this is that should this not be the case, then energy (in the form of Q) will be wasted or gained, resulting in different overall efficiencies every time a cycle is split into component cycles; clearly a cycle can be composed of any number of smaller cycles.
With this understanding of Q1, Q2 and Q3, we note also that mathematically,
-
But the first function is NOT a function of T2, therefore the product of the final two functions MUST result in the removal of T2 as a variable. The only way is therefore to define the function f as follows:
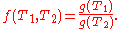
and
so that
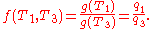
i.e. The ratio of heat exchanged is a function of the respective temperatures at which they occur. We can choose any monotonic function for our
; it is a matter of convenience and convention that we choose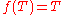 
. Choosing then 1 fixed reference temperature (i.e. triple point of water), we establish the thermodynamic temperature scale.
It is to be noted that such a definition coincides with that of the ideal gas derivation; also it is this definition of the thermodynamic temperature that enables us to represent the Carnot efficiency in terms of TH and TL, and hence derive that the (complete) Carnot cycle is isentropic:
Substituting this back into our first formula for efficiency yields a relationship in terms of temperature:
Notice that for TC=0 the efficiency is 100% and that efficiency becomes greater than 100% for TC. Subtracting the right hand side of Equation 4 from the middle portion and rearranging gives
where the negative sign indicates heat ejected from the system. The generalization of this equation is Clausius theorem, which suggests the existence of a state functionState functionIn thermodynamics, a state function, function of state, state quantity, or state variable is a property of a system that depends only on the current state of the system, not on the way in which the system acquired that state . A state function describes the equilibrium state of a system...
S (i.e., a function which depends only on the state of the system, not on how it reached that state) defined (up to an additive constant) by
where the subscript indicates heat transfer in a reversible process. The function S corresponds to the entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the system, mentioned previously, and the change of S around any cycle is zero (as is necessary for any state function). Equation 5 can be rearranged to get an alternative definition for temperature in terms of entropy and heat (to avoid logic loop, we should first define entropy through statistical mechanics):
For a system in which the entropy S is a function S(E) of its energy E, the thermodynamic temperature T is therefore given by
so that the reciprocal of the thermodynamic temperature is the rate of increase of entropy with energy.
History
- Ca. 485 BC: ParmenidesParmenidesParmenides of Elea was an ancient Greek philosopher born in Elea, a Greek city on the southern coast of Italy. He was the founder of the Eleatic school of philosophy. The single known work of Parmenides is a poem, On Nature, which has survived only in fragmentary form. In this poem, Parmenides...
in his treatise “On Nature” postulated the existente of primum frigidum, a hypothetical elementary substance source of all cooling or cold in the world.
- 1702–1703: Guillaume AmontonsGuillaume AmontonsGuillaume Amontons was a French scientific instrument inventor and physicist. He was one of the pioneers in tribology, apart from Leonardo da Vinci, John Theophilus Desaguliers, Leonard Euler and Charles-Augustin de Coulomb.-Life:Guillaume was born in Paris, France. His father was a lawyer from...
(1663–1705) published two papers that may be used to credit him as being the first researcher to deduce the existence of a fundamental (thermodynamic) temperature scale featuring an absolute zero. He made the discovery while endeavoring to improve upon the air thermometers in use at the time. His J-tube thermometers comprised a mercury column that was supported by a fixed mass of air entrapped within the sensing portion of the thermometer. In thermodynamic terms, his thermometers relied upon the volume / temperature relationship of gas under constant pressure. His measurements of the boiling point of water and the melting point of ice showed that regardless of the mass of air trapped inside his thermometers or the weight of mercury the air was supporting, the reduction in air volume at the ice point was always the same ratio. This observation led him to posit that a sufficient reduction in temperature would reduce the air volume to zero. In fact, his calculations projected that absolute zero was equivalent to −240 °C—only 33.15 degrees short of the true value of −273.15 °C.
- 1742: Anders Celsius
Anders CelsiusAnders Celsius was a Swedish astronomer. He was professor of astronomy at Uppsala University from 1730 to 1744, but traveled from 1732 to 1735 visiting notable observatories in Germany, Italy and France. He founded the Uppsala Astronomical Observatory in 1741, and in 1742 he proposed the Celsius...
(1701–1744) created a "backwards" version of the modern Celsius temperature scale whereby zero represented the boiling point of water and 100 represented the melting point of ice. In his paper Observations of two persistent degrees on a thermometer, he recounted his experiments showing that ice's melting point was effectively unaffected by pressure. He also determined with remarkable precision how water's boiling point varied as a function of atmospheric pressure. He proposed that zero on his temperature scale (water's boiling point) would be calibrated at the mean barometric pressure at mean sea level.
- 1744: Coincident with the death of Anders Celsius, the famous botanist Carolus Linnaeus
.jpg)
Carolus LinnaeusCarl Linnaeus , also known after his ennoblement as , was a Swedish botanist, physician, and zoologist, who laid the foundations for the modern scheme of binomial nomenclature. He is known as the father of modern taxonomy, and is also considered one of the fathers of modern ecology...
(1707–1778) effectively reversed Celsius's scale upon receipt of his first thermometer featuring a scale where zero represented the melting point of ice and 100 represented water's boiling point. The custom-made linnaeus-thermometer, for use in his greenhouses, was made by Daniel Ekström, Sweden's leading maker of scientific instruments at the time. For the next 204 years, the scientific and thermometry communities worldwide referred to this scale as the centigrade scale. Temperatures on the centigrade scale were often reported simply as degrees or, when greater specificity was desired, degrees centigrade. The symbol for temperature values on this scale was °C (in several formats over the years). Because the term centigrade was also the French-language name for a unit of angular measurement (one-hundredth of a right angle) and had a similar connotation in other languages, the term "centesimal degree" was used when very precise, unambiguous language was required by international standards bodies such as the Bureau international des poids et mesuresInternational Bureau of Weights and MeasuresThe International Bureau of Weights and Measures , is an international standards organisation, one of three such organisations established to maintain the International System of Units under the terms of the Metre Convention...
(BIPM). The 9th CGPM (Conférence générale des poids et mesuresGeneral Conference on Weights and MeasuresThe General Conference on Weights and Measures is the English name of the Conférence générale des poids et mesures . It is one of the three organizations established to maintain the International System of Units under the terms of the Convention du Mètre of 1875...
) and the CIPM (Comité international des poids et mesuresInternational Committee for Weights and MeasuresThe Interglobal Committee for Weights and Measures is the English name of the Comité international des poids et mesures . It consists of eighteen persons from Member States of the Metre Convention...
) formally adopted degree Celsius (symbol: °C) in 1948.
- 1777: In his book Pyrometrie (Berlin: Haude & Spener, 1779) completed four months before his death, Johann Heinrich LambertJohann Heinrich LambertJohann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
(1728–1777), sometimes incorrectly referred to as Joseph Lambert, proposed an absolute temperature scale based on the pressure/temperature relationship of a fixed volume of gas. This is distinct from the volume/temperature relationship of gas under constant pressure that Guillaume Amontons discovered 75 years earlier. Lambert stated that absolute zero was the point where a simple straight-line extrapolation reached zero gas pressure and was equal to −270 °C.
- Circa 1787: Notwithstanding the work of Guillaume Amontons 85 years earlier, Jacques Alexandre César CharlesJacques CharlesJacques Alexandre César Charles was a French inventor, scientist, mathematician, and balloonist.Charles and the Robert brothers launched the world's first hydrogen-filled balloon in August 1783, then in December 1783, Charles and his co-pilot Nicolas-Louis Robert ascended to a height of about...
(1746–1823) is often credited with discovering, but not publishing, that the volume of a gas under constant pressure is proportional to its absolute temperature. The formula he created was V1/T1 = V2/T2.
- 1802: Joseph Louis Gay-LussacJoseph Louis Gay-Lussac- External links :* from the American Chemical Society* from the Encyclopædia Britannica, 10th Edition * , Paris...
(1778–1850) published work (acknowledging the unpublished lab notes of Jacques Charles fifteen years earlier) describing how the volume of gas under constant pressure changes linearly with its absolute (thermodynamic) temperature. This behavior is called Charles's LawCharles's lawCharles' law is an experimental gas law which describes how gases tend to expand when heated. It was first published by French natural philosopher Joseph Louis Gay-Lussac in 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles...
and is one of the gas lawsGas lawsThe early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
. His are the first known formulas to use the number 273 for the expansion coefficient of gas relative to the melting point of ice (indicating that absolute zero was equivalent to −273 °C).
- 1848: William Thomson
William Thomson, 1st Baron KelvinWilliam Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
, (1824–1907) also known as Lord Kelvin, wrote in his paper, On an Absolute Thermometric Scale, of the need for a scale whereby infinite cold (absolute zero) was the scale's null point, and which used the degree Celsius for its unit increment. Like Gay-Lussac, Thomson calculated that absolute zero was equivalent to −273 °C on the air thermometers of the time. This absolute scale is known today as the Kelvin thermodynamic temperature scale. It's noteworthy that Thomson's value of −273 was actually derived from 0.00366, which was the accepted expansion coefficient of gas per degree Celsius relative to the ice point. The inverse of −0.00366 expressed to five significant digits is −273.22 °C which is remarkably close to the true value of −273.15 °C.
- 1859: William John Macquorn RankineWilliam John Macquorn RankineWilliam John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....
(1820–1872) proposed a thermodynamic temperature scale similar to William Thomson's but which used the degree FahrenheitFahrenheitFahrenheit is the temperature scale proposed in 1724 by, and named after, the German physicist Daniel Gabriel Fahrenheit . Within this scale, the freezing of water into ice is defined at 32 degrees, while the boiling point of water is defined to be 212 degrees...
for its unit increment. This absolute scale is known today as the Rankine thermodynamic temperature scale.
- 1877–1884: Ludwig Boltzmann
Ludwig BoltzmannLudwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
(1844–1906) made major contributions to thermodynamics through an understanding of the role that particle kinetics and black body radiation played. His name is now attached to several of the formulas used today in thermodynamics.
- Circa 1930s: Gas thermometry experiments carefully calibrated to the melting point of ice and boiling point of water showed that absolute zero was equivalent to −273.15 °C.
- 1948: Resolution 3 of the 9th CGPM (Conférence Générale des Poids et Mesures, also known as the General Conference on Weights and MeasuresGeneral Conference on Weights and MeasuresThe General Conference on Weights and Measures is the English name of the Conférence générale des poids et mesures . It is one of the three organizations established to maintain the International System of Units under the terms of the Convention du Mètre of 1875...
) fixed the triple point of water at precisely 0.01 °C. At this time, the triple point still had no formal definition for its equivalent kelvin value, which the resolution declared "will be fixed at a later date". The implication is that if the value of absolute zero measured in the 1930s was truly −273.15 °C, then the triple point of water (0.01 °C) was equivalent to 273.16 K. Additionally, both the CIPM (Comité international des poids et mesures, also known as the International Committee for Weights and Measures) and the CGPM formally adopted the name Celsius for the degree Celsius and the Celsius temperature scale.
- 1954: Resolution 3 of the 10th CGPM gave the Kelvin scale its modern definition by choosing the triple point of water as its second defining point and assigned it a temperature of precisely 273.16 kelvin (what was actually written 273.16 degrees Kelvin at the time). This, in combination with Resolution 3 of the 9th CGPM, had the effect of defining absolute zero as being precisely zero kelvin and −273.15 °C.
- 1967/1968: Resolution 3 of the 13th CGPM renamed the unit increment of thermodynamic temperature kelvin, symbol K, replacing degree absolute, symbol °K. Further, feeling it useful to more explicitly define the magnitude of the unit increment, the 13th CGPM also decided in Resolution 4 that "The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water".
- 2005: The CIPM (Comité International des Poids et Mesures, also known as the International Committee for Weights and MeasuresInternational Committee for Weights and MeasuresThe Interglobal Committee for Weights and Measures is the English name of the Comité international des poids et mesures . It consists of eighteen persons from Member States of the Metre Convention...
) affirmed that for the purposes of delineating the temperature of the triple point of water, the definition of the Kelvin thermodynamic temperature scale would refer to water having an isotopic composition defined as being precisely equal to the nominal specification of Vienna Standard Mean Ocean Water.
See also
- Absolute hotAbsolute hotAbsolute hot is a concept of temperature that postulates the existence of a highest attainable temperature of matter. The idea has been popularized by the television series Nova...
- Absolute zeroAbsolute zeroAbsolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
- Adiabatic processAdiabatic processIn thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
- Black-bodyBlack bodyA black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
- BoilingBoilingBoiling is the rapid vaporization of a liquid, which occurs when a liquid is heated to its boiling point, the temperature at which the vapor pressure of the liquid is equal to the pressure exerted on the liquid by the surrounding environmental pressure. While below the boiling point a liquid...
- Boltzmann constant
- Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
- Carnot heat engineCarnot heat engineA Carnot heat engine is a hypothetical engine that operates on the reversible Carnot cycle. The basic model for this engine was developed by Nicolas Léonard Sadi Carnot in 1824...
- CelsiusCelsiusCelsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
- Chemical bondChemical bondA chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
- CondensationCondensationCondensation is the change of the physical state of matter from gaseous phase into liquid phase, and is the reverse of vaporization. When the transition happens from the gaseous phase into the solid phase directly, the change is called deposition....
- ConvectionConvectionConvection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
- Degrees of freedomDegrees of freedom (physics and chemistry)A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
- Delocalized electronDelocalized electronIn chemistry, delocalized electrons are electrons in a molecule, ion or solid metal that are not associated with a single atom or one covalent bond....
- DiffusionDiffusionMolecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
- Elastic collisionElastic collisionAn elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter...
- ElectronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
- EnergyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
- Energy conversion efficiencyEnergy conversion efficiencyEnergy conversion efficiency is the ratio between the useful output of an energy conversion machine and the input, in energy terms. The useful output may be electric power, mechanical work, or heat.-Overview:...
- EnthalpyEnthalpyEnthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
- Equipartition theoremEquipartition theoremIn classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
- EvaporationEvaporationEvaporation is a type of vaporization of a liquid that occurs only on the surface of a liquid. The other type of vaporization is boiling, which, instead, occurs on the entire mass of the liquid....
- FahrenheitFahrenheitFahrenheit is the temperature scale proposed in 1724 by, and named after, the German physicist Daniel Gabriel Fahrenheit . Within this scale, the freezing of water into ice is defined at 32 degrees, while the boiling point of water is defined to be 212 degrees...
- First law of thermodynamicsFirst law of thermodynamicsThe first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
- FreezingFreezingFreezing or solidification is a phase change in which a liquid turns into a solid when its temperature is lowered below its freezing point. The reverse process is melting....
- Gas lawsGas lawsThe early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
- HeatHeatIn physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
- Heat conductionHeat conductionIn heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
- Heat engineHeat engineIn thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. It does this by bringing a working substance from a high temperature state to a lower temperature state. A heat "source" generates thermal energy that brings the working substance...
- Internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
- ITS-90International Temperature Scale of 1990The International Temperature Scale of 1990 is an equipment calibration standard for making measurements on the Kelvin and Celsius temperature scales. ITS–90 is an approximation of the thermodynamic temperature scale that facilitates the comparability and compatibility of temperature measurements...
- Ideal gas lawIdeal gas lawThe ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
- JouleJouleThe joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
- KelvinKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
- Kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
- Latent heatLatent heatLatent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was...
- Laws of thermodynamicsLaws of thermodynamicsThe four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
- Maxwell–Boltzmann distribution
- MeltingMeltingMelting, or fusion, is a physical process that results in the phase change of a substance from a solid to a liquid. The internal energy of a substance is increased, typically by the application of heat or pressure, resulting in a rise of its temperature to the melting point, at which the rigid...
- MoleMole (unit)The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
- MoleculeMoleculeA molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
- Orders of magnitude (temperature)Orders of magnitude (temperature)-Detailed list for 100 K to 1000 K:Most ordinary human activity takes place at temperatures of this order of magnitude. Circumstances where water naturally occurs in liquid form are shown in light grey.-External links:*...
- Phase transitionPhase transitionA phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
- PhononPhononIn physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
- Planck's law of black-body radiationPlanck's law of black body radiationIn physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
- Potential energyPotential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
- Quantum mechanics:
- Introduction to quantum mechanicsIntroduction to quantum mechanicsQuantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....
- Quantum mechanics (main article)Quantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
- Introduction to quantum mechanics
- Rankine scale
- Specific heat capacity
- Standard enthalpy change of fusion
- Standard enthalpy change of vaporizationStandard enthalpy change of vaporizationThe enthalpy of vaporization, , also known as the heat of vaporization or heat of evaporation, is the energy required to transform a given quantity of a substance into a gas at a given pressure .It is often measured at the normal boiling point of a substance; although tabulated values are usually...
- Stefan–Boltzmann law
- Sublimation
- TemperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
- Temperature conversion formulasTemperature conversion formulasThis is a compendium of temperature conversion formulæ and comparisons.-Celsius :The simple approximation [°F] = [°C] × 2 + 30 works well within the range of normal weather temperatures, underestimating by 6°F at −20°C and over by 4°F at 30°C.-Comparison:-Comparison of temperature scales:...
- Thermal conductivityThermal conductivityIn physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
- Thermal radiationThermal radiationThermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
- Thermodynamic equationsThermodynamic equationsThermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process...
- Thermodynamic equilibriumThermodynamic equilibriumIn thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
- ThermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
Thermodynamics Category (list of articles)- Timeline of heat engine technologyTimeline of heat engine technologyThis Timeline of heat engine technology describes how heat engines have been known since antiquity but have been made into increasingly useful devices since the seventeenth century as a better understanding of the processes involved was gained...
- Timeline of temperature and pressure measurement technologyTimeline of temperature and pressure measurement technologyTimeline of temperature and pressure measurement technology A history of temperature measurement and pressure measurement technology.-1500s:* 1592-1593 — Galileo Galilei builds a device showing variation of hotness known as the thermoscope using the contraction of air to draw water up a...
- Triple pointTriple pointIn thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
- Universal gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
- Vienna Standard Mean Ocean Water (VSMOW)
- Wien's displacement lawWien's displacement lawWien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
- Work (Mechanical)Mechanical workIn physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
- Work (thermodynamics)Work (thermodynamics)In thermodynamics, work performed by a system is the energy transferred to another system that is measured by the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics. Thermodynamic work encompasses...
- Zero-point energyZero-point energyZero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
External links
- Kinetic Molecular Theory of Gases. An explanation (with interactive animations) of the kinetic motion of molecules and how it affects matter. By David N. Blauch, Department of Chemistry, Davidson College.
- Zero Point Energy and Zero Point Field. A Web site with in-depth explanations of a variety of quantum effects. By Bernard Haisch, of Calphysics Institute.
-
