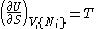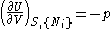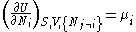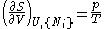Thermodynamic equations
Encyclopedia
Thermodynamics
is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics
.
, or weight lifted through an elevation against gravity, as defined in 1824 by French physicist Sadi Carnot
. Carnot used the phrase motive power
for work. In the footnotes to his famous On the Motive Power of Fire, he states: “We use here the expression motive power to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.” With the inclusion of a unit of time
in Carnot's definition, one arrives at the modern definition for power
:
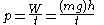
During the latter half of the 19th century, physicists such as Rudolf Clausius
, Peter Guthrie Tait
, and Willard Gibbs worked to develop the concept of a thermodynamic system
and the correlative energetic laws which govern its associated processes. The equilibrium state of a thermodynamic system is described by specifying its "state". The state of a thermodynamic system is specified by a number of extensive quantities
, the most familiar of which are volume, internal energy
, and the amount of each constituent particle (particle number
s). Extensive parameters are properties of the entire system, as contrasted with intensive parameters which can be defined at a single point, such as temperature and pressure. The extensive parameters (except entropy
) are generally conserved in some way as long as the system is "insulated" to changes to that parameter from the outside. The truth of this statement for volume is trivial, for particles one might say that the total particle number of each atomic element is conserved. In the case of energy, the statement of the conservation of energy
is known as the first law of thermodynamics
.
A thermodynamic system is in equilibrium when it is no longer changing in time. This may happen in a very short time, or it may happen with glacial slowness. A thermodynamic system may be composed of many subsystems which may or may not be "insulated" from each other with respect to the various extensive quantities. If we have a thermodynamic system in equilibrium in which we relax some of its constraints, it will move to a new equilibrium state. The thermodynamic parameters may now be thought of as variables and the state may be thought of as a particular point in a space of thermodynamic parameters. The change in the state of the system can be seen as a path in this state space. This change is called a thermodynamic process. Thermodynamic equations are now used to express the relationships between the state parameters at these different equilibrium state.
The concept which governs the path that a thermodynamic system traces in state space as it goes from one equilibrium state to another is that of entropy. The entropy is first viewed as an extensive function of all of the extensive thermodynamic parameters. If we have a thermodynamic system in equilibrium, and we release some of the extensive constraints on the system, there are many equilibrium states that it could move to consistent with the conservation of energy, volume, etc. The second law of thermodynamics
specifies that the equilibrium state that it moves to is in fact the one with the greatest entropy. Once we know the entropy as a function of the extensive variables of the system, we will be able to predict the final equilibrium state.
The conjugate variable pairs are the fundamental state variables used to formulate the thermodynamic functions.
The most important thermodynamic potentials are the following functions:
Thermodynamic system
s are typically affected by the following types of system interactions. The types under consideration are used to classify systems as open systems, closed systems, and isolated systems.
Common material properties
determined from the thermodynamic functions are the following:
The following constants are constants that occur in many relationships due to the application of a standard system of units.
is summarized in the laws of thermodynamics
, which concisely are:
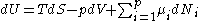
Some important aspects of this equation should be noted: , ,
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
.
Introduction
One of the fundamental thermodynamic equations is the description of thermodynamic work in analogy to mechanical workMechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
, or weight lifted through an elevation against gravity, as defined in 1824 by French physicist Sadi Carnot
Nicolas Léonard Sadi Carnot
Nicolas Léonard Sadi Carnot was a French military engineer who, in his 1824 Reflections on the Motive Power of Fire, gave the first successful theoretical account of heat engines, now known as the Carnot cycle, thereby laying the foundations of the second law of thermodynamics...
. Carnot used the phrase motive power
Motive power
In thermodynamics, motive power is an agency, as water or steam, used to impart motion. Generally, motive power is defined as a natural agent, as water, steam, wind, electricity, etc., used to impart motion to machinery; a motor; a mover. The term may also define something, as a locomotive or a...
for work. In the footnotes to his famous On the Motive Power of Fire, he states: “We use here the expression motive power to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.” With the inclusion of a unit of time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
in Carnot's definition, one arrives at the modern definition for power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
:
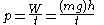
During the latter half of the 19th century, physicists such as Rudolf Clausius
Rudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
, Peter Guthrie Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
, and Willard Gibbs worked to develop the concept of a thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
and the correlative energetic laws which govern its associated processes. The equilibrium state of a thermodynamic system is described by specifying its "state". The state of a thermodynamic system is specified by a number of extensive quantities
Intensive and extensive properties
In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...
, the most familiar of which are volume, internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
, and the amount of each constituent particle (particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
s). Extensive parameters are properties of the entire system, as contrasted with intensive parameters which can be defined at a single point, such as temperature and pressure. The extensive parameters (except entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
) are generally conserved in some way as long as the system is "insulated" to changes to that parameter from the outside. The truth of this statement for volume is trivial, for particles one might say that the total particle number of each atomic element is conserved. In the case of energy, the statement of the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
is known as the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
.
A thermodynamic system is in equilibrium when it is no longer changing in time. This may happen in a very short time, or it may happen with glacial slowness. A thermodynamic system may be composed of many subsystems which may or may not be "insulated" from each other with respect to the various extensive quantities. If we have a thermodynamic system in equilibrium in which we relax some of its constraints, it will move to a new equilibrium state. The thermodynamic parameters may now be thought of as variables and the state may be thought of as a particular point in a space of thermodynamic parameters. The change in the state of the system can be seen as a path in this state space. This change is called a thermodynamic process. Thermodynamic equations are now used to express the relationships between the state parameters at these different equilibrium state.
The concept which governs the path that a thermodynamic system traces in state space as it goes from one equilibrium state to another is that of entropy. The entropy is first viewed as an extensive function of all of the extensive thermodynamic parameters. If we have a thermodynamic system in equilibrium, and we release some of the extensive constraints on the system, there are many equilibrium states that it could move to consistent with the conservation of energy, volume, etc. The second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
specifies that the equilibrium state that it moves to is in fact the one with the greatest entropy. Once we know the entropy as a function of the extensive variables of the system, we will be able to predict the final equilibrium state.
Notation
Some of the most common thermodynamic quantities are:The conjugate variable pairs are the fundamental state variables used to formulate the thermodynamic functions.
| p Pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :... |
V Volume Volume Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains.... |
| T Temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... |
S Entropy Entropy Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when... |
| μ Chemical potential Chemical potential Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system... |
N Particle number Particle number The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle... |
The most important thermodynamic potentials are the following functions:
| U Internal energy Internal energy In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal... |
A Helmholtz free energy Helmholtz free energy In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume... |
H Enthalpy Enthalpy Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a... |
G Gibbs free energy Gibbs free energy In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure... |
Thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
s are typically affected by the following types of system interactions. The types under consideration are used to classify systems as open systems, closed systems, and isolated systems.
| δw infinitesimal amount of Work Mechanical work In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work... (W) |
| δq infinitesimal amount of Heat Heat In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between... (Q) |
| m mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:... |
Common material properties
Material properties (thermodynamics)
The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential...
determined from the thermodynamic functions are the following:
| ρ Rho Rho is the 17th letter of the Greek alphabet. In the system of Greek numerals, it has a value of 100. It is derived from Semitic resh "head"... |
Density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... is defined as mass of material per unit volume |
| CV | Heat capacity Heat capacity Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount... at constant volume |
| Cp | Heat capacity Heat capacity Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount... at constant pressure |
 |
Isothermal compressibility |
 |
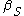Adiabatic compressibility |
 |
Coefficient of thermal expansion Thermal expansion Thermal expansion is the tendency of matter to change in volume in response to a change in temperature.When a substance is heated, its particles begin moving more and thus usually maintain a greater average separation. Materials which contract with increasing temperature are rare; this effect is... |
The following constants are constants that occur in many relationships due to the application of a standard system of units.
| kB Boltzmann constant | R Ideal gas constant Gas constant The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,... |
NA Avogadro constant |
Laws of thermodynamics
The behavior of a thermodynamic systemThermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
is summarized in the laws of thermodynamics
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
, which concisely are:
- Zeroth law of thermodynamicsZeroth law of thermodynamicsThe zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.Systems are said to...
- If A, B, C are thermodynamic systems such that A is in thermal equilibrium with B and B is in thermal equilibrium with C, then A is in thermal equilibrium with C.
-
- The zeroth law is of importance in thermometry, because it implies the existence of temperature scales. In practice, C is a thermometer, and the zeroth law says that systems that are in thermodynamic equilibrium with each other have the same temperature. The law was actually the last of the laws to be formulated.
- First law of thermodynamicsFirst law of thermodynamicsThe first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
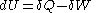where 
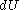is the infinitesimal increase in internal energy of the system, 
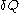is the infinitesimal heat flow into the system, and 
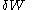is the infinitesimal work done by the system.
- First law of thermodynamics
- The first law is the law of conservation of energyConservation of energyThe nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. The symbol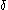
instead of the plain d, originated in the work of German mathematician Carl Gottfried Neumann and is used to denote an inexact differentialInexact differentialAn inexact differential or imperfect differential is a specific type of differential used in thermodynamics to express the path dependence of a particular differential. It is contrasted with the concept of the exact differential in calculus, which can be expressed as the gradient of another...
and to indicate that Q and W are path-dependent (i.e., they are not state functions). In some fields such as physical chemistryPhysical chemistryPhysical chemistry is the study of macroscopic, atomic, subatomic, and particulate phenomena in chemical systems in terms of physical laws and concepts...
, positive work is conventionally considered work done on the system rather than by the system, and the law is expressed as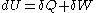
.
- Second law of thermodynamicsSecond law of thermodynamicsThe second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
- The entropy of an isolated system never decreases:
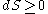for an isolated system.
- The entropy of an isolated system never decreases:
- Second law of thermodynamics
- A concept related to the second law which is important in thermodynamics is that of reversibility. A process within a given isolated system is said to be reversible if throughout the process the entropy never increases (i.e. the entropy remains unchanged).
- Third law of thermodynamicsThird law of thermodynamicsThe third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
-
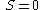when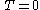 
-
- Third law of thermodynamics
- The third law of thermodynamics states that at the absolute zero of temperature, the entropy is zero for a perfect crystalline structure.
- Onsager reciprocal relationsOnsager reciprocal relationsIn thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists....
– sometimes called the Fourth law of thermodynamics-
; -
.
-
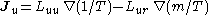- Onsager reciprocal relations
- The fourth law of thermodynamics is not yet an agreed upon law (many supposed variations exist); historically, however, the Onsager reciprocal relations have been frequently referred to as the fourth law.
- The zeroth law is of importance in thermometry, because it implies the existence of temperature scales. In practice, C is a thermometer, and the zeroth law says that systems that are in thermodynamic equilibrium with each other have the same temperature. The law was actually the last of the laws to be formulated.
The fundamental equation
The first and second law of thermodynamics are the most fundamental equations of thermodynamics. They may be combined into what is known as fundamental thermodynamic relation which describes all of the thermodynamic properties of a system. As a simple example, consider a system composed of a number of p different types of particles and has the volume as its only external variable. The fundamental thermodynamic relation may then be expressed in terms of the internal energy as: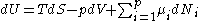Some important aspects of this equation should be noted: , ,
- The thermodynamic space has p+2 dimensions
- The differential quantities (U, S, V, Ni) are all extensive quantities. The coefficients of the differential quantities are intensive quantities (temperature, pressure, chemical potential). Each pair in the equation are known as a conjugate pairConjugate variables (thermodynamics)In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature/entropy or pressure/volume. In fact all thermodynamic potentials are expressed in terms of conjugate pairs....
with respect to the internal energy. The intensive variables may be viewed as a generalized "force". An imbalance in the intensive variable will cause a "flow" of the extensive variable in a direction to counter the imbalance.
- The equation may be seen as a particular case of the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. In other words:
-
- from which the following identifications can be made:
- These equations are known as "equations of state" with respect to the internal energy. (Note - the relation between pressure, volume, temperature, and particle number which is commonly called "the equation of state" is just one of many possible equations of state.) If we know all p+2 of the above equations of state, we may reconstitute the fundamental equation and recover all thermodynamic properties of the system.
- The fundamental equation can be solved for any other differential and similar expressions can be found. For example, we may solve for
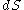and find that
Thermodynamic potentials
By the principle of minimum energyPrinciple of minimum energyThe principle of minimum energy is essentially a restatement of the second law of thermodynamics. It states that for a closed system, with constant external parameters and entropy, the internal energy will decrease and approach a minimum value at equilibrium...
, the second law can be restated by saying that for a fixed entropy, when the constraints on the system are relaxed, the internal energy assumes a minimum value. This will require that the system be connected to its surroundings, since otherwise the energy would remain constant.
By the principle of minimum energy, there are a number of other state functions which may be defined which have the dimensions of energy and which are minimized according to the second law under certain conditions other than constant entropy. These are called thermodynamic potentialsThermodynamic potentialsA thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
. The four most common thermodynamic potentials are:
After each potential is shown its "natural variables". These variables are important because if the thermodynamic potential is expressed in terms of its natural variables, then it will contain all of the thermodynamic relationships necessary to derive any other relationship. In other words, it too will be a fundamental equation. For the above four potentials, the fundamental equations are expressed as:
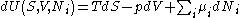
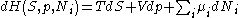
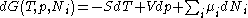
The thermodynamic squareThermodynamic squareThe thermodynamic square is a mnemonic diagram used to help determine thermodynamic relations. The corners represent common conjugate variables while the sides represent thermodynamic potentials...
can be used as a tool to recall and derive these potentials.
First order equations
- General system
- Particular systems
Just as with the internal energy version of the fundamental equation, the chain rule can be used on the above equations to find p+2 equations of state with respect to the particular potential. If Φ is a thermodynamic potential, then the fundamental equation may be expressed as:
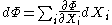
where the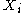
are the natural variables of the potential. If 
is conjugate to 
then we have the equations of state for that potential, one for each set of conjugate variables.
Only one equation of state will not be sufficient to reconstitute the fundamental equation. All equations of state will be needed to fully characterize the thermodynamic system. Note that what is commonly called "the equation of state" is just the "mechanical" equation of state involving the Helmholtz potential and the volume:
For an ideal gas, this becomes the familiar PV=NkT.
Euler integrals
Because all of natural variables of the internal energy U are extensive quantities, it follows from Euler's homogeneous function theoremHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
that
Substituting into the expressions for the other main potentials we have the following expressions for the thermodynamic potentials:
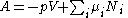
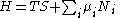
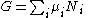
Note that the Euler integrals are sometimes also referred to as fundamental equations.
Gibbs–Duhem relationship
Differentiating the Euler equation for the internal energy and combining with the fundamental equation for internal energy, it follows that:
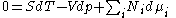
which is known as the Gibbs-Duhem relationship. The Gibbs-Duhem is a relationship among the intensive parameters of the system. It follows that for a simple system with r components, there will be r+1 independent parameters, or degrees of freedom. For example, a simple system with a single component will have two degrees of freedom, and may be specified by only two parameters, such as pressure and volume for example. The law is named after Josiah Gibbs and Pierre DuhemPierre DuhemPierre Maurice Marie Duhem was a French physicist, mathematician and philosopher of science, best known for his writings on the indeterminacy of experimental criteria and on scientific development in the Middle Ages...
.
Second order equations
There are many relationships that follow mathematically from the above basic equations. See Exact differentialExact differentialA mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q....
for a list of mathematical relationships. Many equations are expressed as second derivatives of the thermodynamic potentials (see Bridgman equations).
Maxwell relations
Maxwell relationsMaxwell relationsMaxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...
are equalities involving the second derivatives of thermodynamic potentials with respect to their natural variables. They follow directly from the fact that the order of differentiation does not matter when taking the second derivative. The four most common Maxwell relations are:
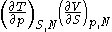
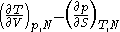
The thermodynamic squareThermodynamic squareThe thermodynamic square is a mnemonic diagram used to help determine thermodynamic relations. The corners represent common conjugate variables while the sides represent thermodynamic potentials...
can be used as a tool to recall and derive these relations.
Material properties
Second derivatives of thermodynamic potentials generally describe the response of the system to small changes. The number of second derivatives which are independent of each other is relatively small, which means that most material properties can be described in terms of just a few "standard" properties. For the case of a single component system, there are three properties generally considered "standard" from which all others may be derived:
- Compressibility at constant temperature or constant entropy
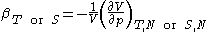
- Heat capacityHeat capacityHeat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
at constant pressure or constant volume
- Coefficient of thermal expansion
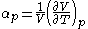
These properties are seen to be the three possible second derivative of the Gibbs free energy with respect to temperature and pressure.
