
Maxwell relations
Encyclopedia
Maxwell's relations are a set of equations in thermodynamics
which are derivable from the definitions of the thermodynamic potentials
. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of differentiation of an analytic function
of two variables is irrelevant. If Φ is a thermodynamic potential and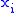 and
and 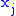 are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is:
are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is:
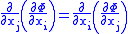
where the partial derivatives are taken with all other natural variables held constant. It is seen that for every thermodynamic potential there are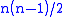 possible Maxwell relations where n is the number of natural variables for that potential.
possible Maxwell relations where n is the number of natural variables for that potential.
These relations are named for the nineteenth-century physicist James Clerk Maxwell
.
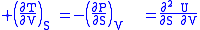
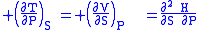
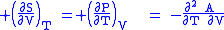
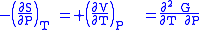
where the potentials as functions of their natural thermal and mechanical variables are:
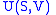 - The internal energy
- The internal energy
 - The Enthalpy
- The Enthalpy
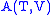 - The Helmholtz free energy
- The Helmholtz free energy
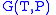 - The Gibbs free energy
- The Gibbs free energy
The thermodynamic square
can be used as a tool to recall and derive these relations.


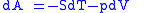
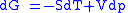
These equations resemble total differentials of the form

And indeed, it can be shown that for any equation of the form
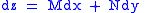
that
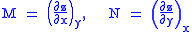
Consider, as an example, the equation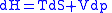 . We can now immediately see that
. We can now immediately see that

Since we also know that for functions with continuous second derivatives, the mixed partial derivatives are identical (Symmetry of second derivatives
), that is, that
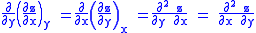
we therefore can see that
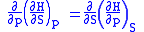
and therefore that
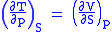
Each of the four Maxwell relationships given above follows similarly from one of the Gibbs equations
Combined form first and second law of thermodynamics,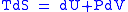 (Eq.1)
(Eq.1)
U, S, and V are state functions.
Let,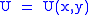
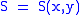
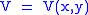
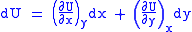

Substitute them in Eq.1 and one gets,
And also written as,
comparing the coefficient of dx and dy, one gets
Differentiating above equations by y, x respectively
 (Eq.2)
(Eq.2)
U, S, and V are exact differentials, therefore,

Subtract eqn(2) and (3) and one gets
Maxwell's first relation
Maxwell's second relation
Maxwell's third relation
Maxwell's fourth relation
Maxwell's fifth relation
Maxwell's sixth relation
is included as a natural variable, other Maxwell relations become apparent. For example, if we have a single-component gas, then the number of particles N is also a natural variable of the above four thermodynamic potentials. The Maxwell relationship for the enthalpy with respect to pressure and particle number would then be:
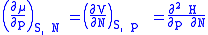
where μ is the chemical potential
. In addition, there are other thermodynamic potentials besides the four that are commonly used, and each of these potentials will yield a set of Maxwell relations.
Each equation can be re-expressed using the relationship
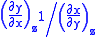
which are sometimes also known as Maxwell relations.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
which are derivable from the definitions of the thermodynamic potentials
Thermodynamic potentials
A thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of differentiation of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of two variables is irrelevant. If Φ is a thermodynamic potential and
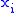 and
and 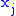 are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is:
are two different natural variables for that potential, then the Maxwell relation for that potential and those variables is: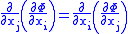
where the partial derivatives are taken with all other natural variables held constant. It is seen that for every thermodynamic potential there are
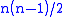 possible Maxwell relations where n is the number of natural variables for that potential.
possible Maxwell relations where n is the number of natural variables for that potential.These relations are named for the nineteenth-century physicist James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
.
The four most common Maxwell relations
The four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature T or entropy S ) and their mechanical natural variable (pressure P or volume V ):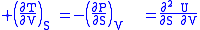
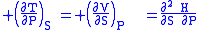
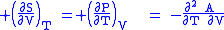
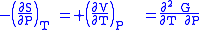
where the potentials as functions of their natural thermal and mechanical variables are:
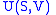 - The internal energy
- The internal energyInternal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
 - The Enthalpy
- The EnthalpyEnthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
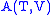 - The Helmholtz free energy
- The Helmholtz free energyHelmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
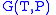 - The Gibbs free energy
- The Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
The thermodynamic square
Thermodynamic square
The thermodynamic square is a mnemonic diagram used to help determine thermodynamic relations. The corners represent common conjugate variables while the sides represent thermodynamic potentials...
can be used as a tool to recall and derive these relations.
Derivation of the Maxwell relations
Derivation of the Maxwell relations can be deduced from the differential forms of the thermodynamic potentials:

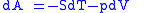
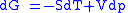
These equations resemble total differentials of the form

And indeed, it can be shown that for any equation of the form
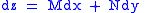
that
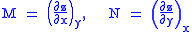
Consider, as an example, the equation
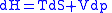 . We can now immediately see that
. We can now immediately see that
Since we also know that for functions with continuous second derivatives, the mixed partial derivatives are identical (Symmetry of second derivatives
Symmetry of second derivatives
In mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
), that is, that
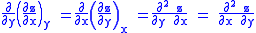
we therefore can see that
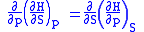
and therefore that
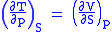
Each of the four Maxwell relationships given above follows similarly from one of the Gibbs equations
Extended derivation of the Maxwell relations
Maxwell relations are based on simple partial differentiation rules.Combined form first and second law of thermodynamics,
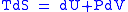 (Eq.1)
(Eq.1)U, S, and V are state functions.
Let,
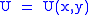
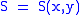
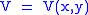
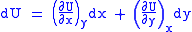

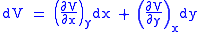
Substitute them in Eq.1 and one gets,
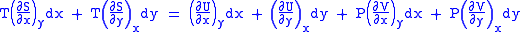
And also written as,

comparing the coefficient of dx and dy, one gets

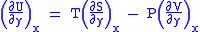
Differentiating above equations by y, x respectively
 (Eq.2)
(Eq.2)
- and
 (Eq.3)
(Eq.3)
U, S, and V are exact differentials, therefore,


Subtract eqn(2) and (3) and one gets
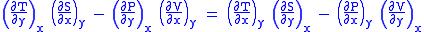
- Note: The above is called the general expression for Maxwell's thermodynamical relation.
Maxwell's first relation
- Allow x = S and y = V and one gets
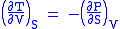
Maxwell's second relation
- Allow x = T and y = V and one gets

Maxwell's third relation
- Allow x = S and y = P and one gets
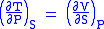
Maxwell's fourth relation
- Allow x = T and y = P and one gets
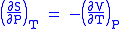
Maxwell's fifth relation
- Allow x = P and y = V

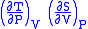 = 1
= 1
Maxwell's sixth relation
- Allow x = T and y = S and one gets
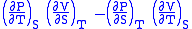 = 1
= 1
General Maxwell relationships
The above are by no means the only Maxwell relationships. When other work terms involving other natural variables besides the volume work are considered or when the number of particlesParticle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
is included as a natural variable, other Maxwell relations become apparent. For example, if we have a single-component gas, then the number of particles N is also a natural variable of the above four thermodynamic potentials. The Maxwell relationship for the enthalpy with respect to pressure and particle number would then be:
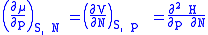
where μ is the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. In addition, there are other thermodynamic potentials besides the four that are commonly used, and each of these potentials will yield a set of Maxwell relations.
Each equation can be re-expressed using the relationship
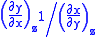
which are sometimes also known as Maxwell relations.
See also
- Table of thermodynamic equationsTable of thermodynamic equationsThe following page is a concise list of common thermodynamic equations and quantities:-Entropy:*~ S = k_B ~, where k_B is the Boltzmann constant, and \Omega denotes the volume of macrostate in the phase space....
- Thermodynamic equationsThermodynamic equationsThermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process...
- Thermodynamic potentialsThermodynamic potentialsA thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
External links
- http://theory.ph.man.ac.uk/~judith/stat_therm/node48.html a partial derivation of Maxwell's relations

