Inexact differential
Encyclopedia
An inexact differential or imperfect differential is a specific type of differential used in thermodynamics to express the path dependence of a particular differential. It is contrasted with the concept of the exact differential
in calculus
, which can be expressed as the gradient of another function and is therefore path independent. Consequently, an inexact differential cannot be expressed in terms of its antiderivative
for the purpose of integral calculations i.e. its value cannot be inferred just by looking at the initial and final states of a given system.. It is primarily used in calculations involving heat
and work because they are not state functions.
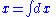. However, this is technically incorrect because the differential dx is one-dimensional and therefore cannot be inexact (See below). More precisely, an inexact differential is a function that cannot be expressed as the gradient
of another function. In the language of calculus, for a given vector field F in 3-dimensional space, dF is an inexact differential if there is no function f such that
The fundamental theorem of calculus for line integrals
requires path independence in order to express the values of a given vector field in terms of the partial derivatives of another function that is the multivariate analogue of the antiderivative. This is because there can be no unique representation of an antiderivative for inexact differentials since their variation is inconsistent along different paths. This stipulation of path independence is a necessary addendum to the fundamental theorem of calculus
because in one-dimensional calculus there is only one path in between two points defined by a function.
Inexact differentials are known especially for their presence in the first law of thermodynamics
:
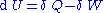
The symbol δ instead of the plain d, which originated from the work of German mathematician Carl Gottfried Neumann indicates that Q and W are path-dependent.
Internal energy U is a state function
, meaning its change can be inferred just by comparing two different states of the system (not its transition path), which we can therefore indicate with U1 and U2.
Since we can go from state U1 to state U2 either by providing heat Q = U2 − U1 or work W = U2 − U1, such a change of state does not identify uniquely the values of provided W and Q, but only the change in internal energy ΔU.
The easiest example would be to consider the difference between net distance and total distance. For example, in walking from Point A to Point B one covers a net distance B-A that is equal to the total distance. If one then returns to Point A, however, net distance is now 0 while total distance covered is 2*(B-A). Although rather imprecise, this example captures the essential idea behind the inexact differential.
There are many everyday examples that are much more relevant to inexact differentials in the actual context in which it is used.
It is known that, with some skill, it is possible to start a fire
only using friction
and tinder
. This is a way to convert mechanical energy (work, W) into an increase of internal energy, ΔU, which finally results into an increase in the local temperature of wood, its gasification and combustion
, thereby creating a fire.
It is also possible to start a fire by adding heat using a lighter. This is a way to convert heat (Q) into an increase of internal energy, ΔU, but it has the same result as in the example involving work.
Both friction and heat transfer increase the internal energy of the system, since heat is a form of energy.
Therefore, the sum of exchanged heat and work is an exact differential (dU), but since they are equivalent and the lack of one can be compensated by the presence of the other, singularly they are inexact differentials. In other words, specifying the change in internal energy alone is insufficient to determine the heat evolved or the work done because there is no differentiation between the two forms of energy.
.
The most common example of this in thermodynamics is the definition of entropy
:
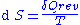
In this case, δQ is an inexact differential, because its effect on the state of the system can be compensated by δW.
However, when divided by the absolute temperature
and when the exchange occurs at reversible conditions (therefore the rev subscript), it produces an exact differential: the entropy S is also a state function.
Exact differential
A mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q....
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, which can be expressed as the gradient of another function and is therefore path independent. Consequently, an inexact differential cannot be expressed in terms of its antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
for the purpose of integral calculations i.e. its value cannot be inferred just by looking at the initial and final states of a given system.. It is primarily used in calculations involving heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
and work because they are not state functions.
Definition
An inexact differential is commonly defined as a differential form dx where there is no corresponding function x such that :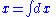. However, this is technically incorrect because the differential dx is one-dimensional and therefore cannot be inexact (See below). More precisely, an inexact differential is a function that cannot be expressed as the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of another function. In the language of calculus, for a given vector field F in 3-dimensional space, dF is an inexact differential if there is no function f such that
The fundamental theorem of calculus for line integrals
Gradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
requires path independence in order to express the values of a given vector field in terms of the partial derivatives of another function that is the multivariate analogue of the antiderivative. This is because there can be no unique representation of an antiderivative for inexact differentials since their variation is inconsistent along different paths. This stipulation of path independence is a necessary addendum to the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
because in one-dimensional calculus there is only one path in between two points defined by a function.
First law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
:
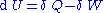
The symbol δ instead of the plain d, which originated from the work of German mathematician Carl Gottfried Neumann indicates that Q and W are path-dependent.
Internal energy U is a state function
State function
In thermodynamics, a state function, function of state, state quantity, or state variable is a property of a system that depends only on the current state of the system, not on the way in which the system acquired that state . A state function describes the equilibrium state of a system...
, meaning its change can be inferred just by comparing two different states of the system (not its transition path), which we can therefore indicate with U1 and U2.
Since we can go from state U1 to state U2 either by providing heat Q = U2 − U1 or work W = U2 − U1, such a change of state does not identify uniquely the values of provided W and Q, but only the change in internal energy ΔU.
Examples
Although difficult to express mathematically, the inexact differential is very simple conceptually.The easiest example would be to consider the difference between net distance and total distance. For example, in walking from Point A to Point B one covers a net distance B-A that is equal to the total distance. If one then returns to Point A, however, net distance is now 0 while total distance covered is 2*(B-A). Although rather imprecise, this example captures the essential idea behind the inexact differential.
There are many everyday examples that are much more relevant to inexact differentials in the actual context in which it is used.
It is known that, with some skill, it is possible to start a fire
Fire
Fire is the rapid oxidation of a material in the chemical process of combustion, releasing heat, light, and various reaction products. Slower oxidative processes like rusting or digestion are not included by this definition....
only using friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
and tinder
Tinder
Tinder is easily combustible material used to ignite fires by rudimentary methods. A small fire consisting of tinder is then used to ignite kindling. Anything that can be ignited by a match can be considered tinder; or by more rigorous definition, anything that begins to glow under a shower of...
. This is a way to convert mechanical energy (work, W) into an increase of internal energy, ΔU, which finally results into an increase in the local temperature of wood, its gasification and combustion
Combustion
Combustion or burning is the sequence of exothermic chemical reactions between a fuel and an oxidant accompanied by the production of heat and conversion of chemical species. The release of heat can result in the production of light in the form of either glowing or a flame...
, thereby creating a fire.
It is also possible to start a fire by adding heat using a lighter. This is a way to convert heat (Q) into an increase of internal energy, ΔU, but it has the same result as in the example involving work.
Both friction and heat transfer increase the internal energy of the system, since heat is a form of energy.
Therefore, the sum of exchanged heat and work is an exact differential (dU), but since they are equivalent and the lack of one can be compensated by the presence of the other, singularly they are inexact differentials. In other words, specifying the change in internal energy alone is insufficient to determine the heat evolved or the work done because there is no differentiation between the two forms of energy.
Integrating factors
It is sometime possible to convert an inexact differential into an exact one by means of an integrating factorIntegrating factor
In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
.
The most common example of this in thermodynamics is the definition of entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
:
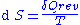
In this case, δQ is an inexact differential, because its effect on the state of the system can be compensated by δW.
However, when divided by the absolute temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and when the exchange occurs at reversible conditions (therefore the rev subscript), it produces an exact differential: the entropy S is also a state function.
See also
- Closed and exact differential formsClosed and exact differential formsIn mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
for a higher-level treatment - Differential (mathematics)Differential (mathematics)In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
- Exact differentialExact differentialA mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q....
- Integrating factorIntegrating factorIn mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
for solving non-exact differential equations by making them exact
External links
- Inexact Differential – from Wolfram MathWorld
- Exact and Inexact Differentials – University of Arizona
- Exact and Inexact Differentials – University of Texas
- Exact Differential – from Wolfram MathWorld