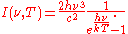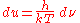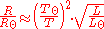Stefan-Boltzmann law
Encyclopedia
The Stefan–Boltzmann law, also known as Stefan's law, states that the total energy
radiated per unit surface area
of a black body
per unit time
(also known as the black-body irradiance
or emissive power), j*, is directly proportional
to the fourth power of the black body's thermodynamic temperature
T (also called absolute temperature):

The constant of proportionality σ, called the Stefan–Boltzmann constant or Stefan's constant, derives from other known constants of nature. The value of the constant is
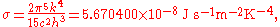
where k is the Boltzmann constant, h is Planck's constant, and c is the speed of light in a vacuum
. Thus at 100 K the energy flux density is 5.67 W/m2, at 1000 K 56,700 W/m2, etc.
A more general case is of a grey body, the one that doesn't absorb or emit the full amount of radiative flux. Instead, it radiates a portion of it, characterized by its emissivity
, :
:
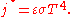
The irradiance j* has dimensions of energy flux (energy per time per area), and the SI
units of measure are joule
s per second per square metre, or equivalently, watt
s per square metre. The SI unit for absolute temperature T is the kelvin
. is the emissivity
is the emissivity
of the grey body; if it is a perfect blackbody, . Still in more general (and realistic) case, the emissivity depends on the wavelength,
. Still in more general (and realistic) case, the emissivity depends on the wavelength,  .
.
To find the total absolute power
of energy
radiated for an object we have to take into account the surface area, A(in m2):

The law was deduced by Jožef Stefan
(1835–1893) in 1879 on the basis of experimental measurements made by John Tyndall
and was derived from theoretical considerations, using thermodynamics
, by Ludwig Boltzmann
(1844–1906) in 1884. Boltzmann considered a certain ideal heat engine
with light
as a working matter instead of gas. The law is valid only for ideal black objects, the perfect radiators, called black bodies
. Stefan published this law in the article Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (On the relationship between thermal radiation and temperature) in the Bulletins from the sessions of the Vienna Academy of Sciences.
surface radiating out into a half-sphere. This derivation uses spherical coordinates, with φ as the zenith angle and θ as the azimuthal angle; and the small flat blackbody surface lies on the xy-plane, where φ = π/2.
The intensity of the light emitted from the blackbody surface is given by Planck's law :
The quantity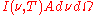 is the power
is the power
radiated by a surface of area A through a solid angle
dΩ in the frequency range .
.
The Stefan–Boltzmann law gives the power emitted per unit area of the emitting body,
To derive the Stefan–Boltzmann law, we must integrate Ω over the half-sphere and integrate ν from 0 to ∞. Furthermore, because black bodies are Lambertian (i.e. they obey Lambert's cosine law
), the intensity observed along the sphere will be the actual intensity times the cosine of the zenith angle φ, and in spherical coordinates, dΩ = sin(φ) dφ dθ.
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
radiated per unit surface area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
per unit time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
(also known as the black-body irradiance
Irradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
or emissive power), j*, is directly proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the fourth power of the black body's thermodynamic temperature
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
T (also called absolute temperature):

The constant of proportionality σ, called the Stefan–Boltzmann constant or Stefan's constant, derives from other known constants of nature. The value of the constant is
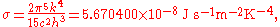
where k is the Boltzmann constant, h is Planck's constant, and c is the speed of light in a vacuum
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. Thus at 100 K the energy flux density is 5.67 W/m2, at 1000 K 56,700 W/m2, etc.
A more general case is of a grey body, the one that doesn't absorb or emit the full amount of radiative flux. Instead, it radiates a portion of it, characterized by its emissivity
Emissivity
The emissivity of a material is the relative ability of its surface to emit energy by radiation. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature...
,
 :
: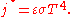
The irradiance j* has dimensions of energy flux (energy per time per area), and the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units of measure are joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s per second per square metre, or equivalently, watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s per square metre. The SI unit for absolute temperature T is the kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
.
 is the emissivity
is the emissivityEmissivity
The emissivity of a material is the relative ability of its surface to emit energy by radiation. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature...
of the grey body; if it is a perfect blackbody,
 . Still in more general (and realistic) case, the emissivity depends on the wavelength,
. Still in more general (and realistic) case, the emissivity depends on the wavelength,  .
.To find the total absolute power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
radiated for an object we have to take into account the surface area, A(in m2):

The law was deduced by Jožef Stefan
Joseph Stefan
Joseph Stefan was a physicist, mathematician, and poet of Slovene mother tongue and Austrian citizenship.- Life and work :...
(1835–1893) in 1879 on the basis of experimental measurements made by John Tyndall
John Tyndall
John Tyndall FRS was a prominent Irish 19th century physicist. His initial scientific fame arose in the 1850s from his study of diamagnetism. Later he studied thermal radiation, and produced a number of discoveries about processes in the atmosphere...
and was derived from theoretical considerations, using thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, by Ludwig Boltzmann
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
(1844–1906) in 1884. Boltzmann considered a certain ideal heat engine
Heat engine
In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. It does this by bringing a working substance from a high temperature state to a lower temperature state. A heat "source" generates thermal energy that brings the working substance...
with light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
as a working matter instead of gas. The law is valid only for ideal black objects, the perfect radiators, called black bodies
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
. Stefan published this law in the article Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (On the relationship between thermal radiation and temperature) in the Bulletins from the sessions of the Vienna Academy of Sciences.
Integration of intensity derivation
The law can be derived by considering a small flat black bodyBlack body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
surface radiating out into a half-sphere. This derivation uses spherical coordinates, with φ as the zenith angle and θ as the azimuthal angle; and the small flat blackbody surface lies on the xy-plane, where φ = π/2.
The intensity of the light emitted from the blackbody surface is given by Planck's law :
-
- where
 is the amount of energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is the amount of energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
per unit surface areaSurface areaSurface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
per unit timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
per unit solid angleSolid angleThe solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
emitted in the frequency range between ν and ν + dν by a black body at temperature T is Planck's constant
is Planck's constant is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, and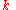 is Boltzmann's constant.
is Boltzmann's constant.
The quantity
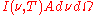 is the power
is the powerPower (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
radiated by a surface of area A through a solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
dΩ in the frequency range
 .
.The Stefan–Boltzmann law gives the power emitted per unit area of the emitting body,
To derive the Stefan–Boltzmann law, we must integrate Ω over the half-sphere and integrate ν from 0 to ∞. Furthermore, because black bodies are Lambertian (i.e. they obey Lambert's cosine law
Lambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
), the intensity observed along the sphere will be the actual intensity times the cosine of the zenith angle φ, and in spherical coordinates, dΩ = sin(φ) dφ dθ.
-
-

Then we plug in for I:
To do this integral, do a substitution,
which gives:
The integral on the right can be done in a number of ways (one is included in this article's appendix) – its answer is π4/15, giving the result that, for a perfect blackbody surface:
An alternative form of the Stefan–Boltzmann constant, more fundamental to physics:
Finally, this proof started out only considering a small flat surface. However, any differentiable surface can be approximated by a bunch of small flat surfaces. So long as the geometry of the surface does not cause the blackbody to reabsorb its own radiation, the total energy radiated is just the sum of the energies radiated by each surface; and the total surface area is just the sum of the areas of each surface—so this law holds for all convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
blackbodies, too, so long as the surface has the same temperature throughout.
Thermodynamic derivation
The fact that the energy density of the box containing radiation is proportional to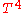 can be derived using thermodynamics. It follows from classical electrodynamics that the radiation pressure
can be derived using thermodynamics. It follows from classical electrodynamics that the radiation pressure 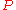 is related to the internal energy density:
is related to the internal energy density:
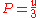
The total internal energy of the box containing radiation can thus be written as:
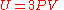
Inserting this in the fundamental thermodynamic relation

yields
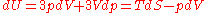
so
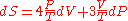
This equation can be used to derive a Maxwell relationMaxwell relationsMaxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...
. From the above equation it can be seen that:
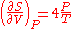
and

The symmetry of second derivativesSymmetry of second derivativesIn mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
of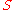 with regard to
with regard to  and
and  then implies:
then implies:
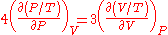
Because the pressure is proportional to the internal energy density it depends only on the temperature and not on the volume. In the derivative on the right hand side, the temperature is thus a constant. Evaluating the derivatives gives the differential equation:
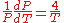
This can be solved by integrating with respect to T to give
This implies that
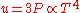
Temperature of the Sun
With his law Stefan also determined the temperature of the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
's surface. He learned from the data of Charles SoretCharles SoretCharles Soret was a Swiss physicist and chemist. He is universally known for his work on thermodiffusion .-Life:...
(1854–1904) that the energy flux density from the Sun is 29 times greater than the energy flux density of a warmed metal lamella. A round lamella was placed at such a distance from the measuring device that it would be seen at the same angle as the Sun. Soret estimated the temperature of the lamella to be approximately 1900 °CCelsiusCelsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
to 2000 °C. Stefan surmised that ⅓ of the energy flux from the Sun is absorbed by the Earth's atmosphereEarth's atmosphereThe atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
, so he took for the correct Sun's energy flux a value 3/2 times greater, namely 29 × 3/2 = 43.5.
Precise measurements of atmospheric absorptionAbsorption (electromagnetic radiation)In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...
were not made until 1888 and 1904. The temperature Stefan obtained was a median value of previous ones, 1950 °C and the absolute thermodynamic one 2200 K. As 2.574 = 43.5, it follows from the law that the temperature of the Sun is 2.57 times greater than the temperature of a lamella, so Stefan got a value of 5430 °C or 5700 K (the modern value is 5778 K). This was the first sensible value for the temperature of the Sun. Before this, values ranging from as low as 1800 °C to as high as 13,000,000 °C were claimed. The lower value of 1800 °C was determined by Claude Servais Mathias PouilletClaude Servais Mathias PouilletClaude Servais Mathias Pouillet was a French physicist and a professor of physics at the Sorbonne and member of the French Academy of Science.Pouillet was born in Cusance, Doubs, France....
(1790–1868) in 1838 using the Dulong-Petit law. Pouilet also took just half the value of the Sun's correct energy flux.
Temperature of stars
The temperature of starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s other than the Sun can be approximated using a similar means by treating the emitted energy as a black bodyBlack bodyA black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiation. So:
where L is the luminosityLuminosityLuminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
, σ is the Stefan–Boltzmann constant, R is the stellar radius and T is the effective temperatureEffective temperatureThe effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
. This same formula can be used to compute the approximate radius of a main sequence star relative to the sun:
where , is the solar radius, and so forth.
, is the solar radius, and so forth.
With the Stefan–Boltzmann law, astronomerAstronomerAn astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
s can easily infer the radii of stars. The law is also met in the thermodynamicsBlack hole thermodynamicsIn physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
of black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s in so-called Hawking radiationHawking radiationHawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
.
Temperature of the Earth
Similarly we can calculate the effective temperatureEffective temperatureThe effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
of the Earth TE by equating the energy received from the Sun and the energy radiated by the Earth, under the black-body approximation. The amount of energy, ES, emitted by the Sun is given by:
At Earth, this energy is passing through a sphere with a radius of a0, the distance between the Earth and the Sun, and the energy passing through each square metre of the sphere is given by
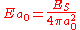
The Earth has a radius of rE, and therefore has a cross-section of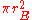 . The amount of solar energy absorbed by the Earth is thus given by:
. The amount of solar energy absorbed by the Earth is thus given by:
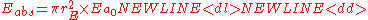
-
The amount of energy emitted must equal the amount of energy absorbed, and so:

TE can then be found:
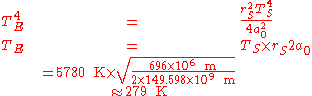
where TS is the temperature of the Sun, rS the radius of the Sun, and a0 is the distance between the Earth and the Sun. This gives an effective temperature of 6°C on the surface of the Earth, assuming that it perfectly absorbs all emission falling on it and has no atmosphere.
The Earth has an albedoAlbedoAlbedo , or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it...
of 0.3, meaning that 30% of the solar radiation that hits the planet gets scattered back into space without absorption. The effect of albedo on temperature can be approximated by assuming that the energy absorbed is multiplied by 0.7, but that the planet still radiates as a black body (the latter by definition of effective temperatureEffective temperatureThe effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
, which is what we are calculating). This approximation reduces the temperature by a factor of 0.71/4, giving 255 K (−18 °C).
However, long-wave radiation from the surface of the earth is partially reflected (or absorbed and re-radiated back down) in the atmosphere, instead of being radiated away, by greenhouse gases, namely water vaporWater vaporWater vapor or water vapour , also aqueous vapor, is the gas phase of water. It is one state of water within the hydrosphere. Water vapor can be produced from the evaporation or boiling of liquid water or from the sublimation of ice. Under typical atmospheric conditions, water vapor is continuously...
, carbon dioxideCarbon dioxideCarbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...
and methaneMethaneMethane is a chemical compound with the chemical formula . It is the simplest alkane, the principal component of natural gas, and probably the most abundant organic compound on earth. The relative abundance of methane makes it an attractive fuel...
. Since the emissivity with greenhouse effect (weighted more in the longer wavelengths where the Earth radiates) is reduced more than the absorptivity (weighted more in the shorter wavelengths of the Sun's radiation) is reduced, the equilibrium temperature is higher than the simple black-body calculation estimates. As a result, the Earth's actual average surface temperature is about 288 K (14 °C), which is higher than the 255 K effective temperature, and even higher than the 279 K temperature that a black body would have.
Appendix
In one of the above derivations, the following integral appeared:

where is the polylogarithm function and
is the polylogarithm function and 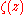 is the Riemann zeta function. If the polylogarithm function and the Riemann zeta function are not available for calculation, there are a number of ways to do this integration; a simple one is given in the appendix of the Planck's law article. This appendix does the integral by contour integration. Consider the function:
is the Riemann zeta function. If the polylogarithm function and the Riemann zeta function are not available for calculation, there are a number of ways to do this integration; a simple one is given in the appendix of the Planck's law article. This appendix does the integral by contour integration. Consider the function:
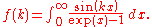
Using the Taylor expansion of the sine function, it should be evident that the coefficient of the k3 term would be exactly -J/6.
By expanding both sides in powers of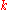 , we see that
, we see that 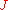 is minus 6 times the coefficient of
is minus 6 times the coefficient of 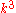 of the series expansion of
of the series expansion of 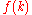 . So, if we can find a closed form for f(k), its Taylor expansion will give J.
. So, if we can find a closed form for f(k), its Taylor expansion will give J.
In turn, sin(x) is the imaginary part of eix, so we can restate this as:
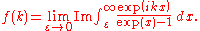
To evaluate the integral in this equation we consider the contour integral:
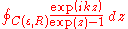
where is the contour from
is the contour from  to
to  , then to
, then to 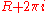 , then to
, then to  , then we go to the point
, then we go to the point  , avoiding the pole at
, avoiding the pole at  by taking a clockwise quarter circle with radius
by taking a clockwise quarter circle with radius  and center
and center  . From there we go to
. From there we go to 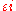 , and finally we return to
, and finally we return to  , avoiding the pole at zero by taking a clockwise quarter circle with radius
, avoiding the pole at zero by taking a clockwise quarter circle with radius  and center zero.
and center zero.
Because there are no poles in the integration contour we have:

We now take the limit . In this limit the contribution from the segment from
. In this limit the contribution from the segment from  to
to 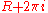 tends to zero. Taking together the integrations over the segments from
tends to zero. Taking together the integrations over the segments from  to
to  and from
and from  to
to 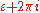 and using the fact that the integrations over clockwise quarter circles withradius
and using the fact that the integrations over clockwise quarter circles withradius  about simple poles are given up to order
about simple poles are given up to order  by minus
by minus 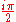 times the residues at the poles we find:
times the residues at the poles we find:

The left hand side is the sum of the integral from to
to  and from
and from 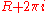 to
to  . We can rewrite the integrand of the integral on the r.h.s. as follows:
. We can rewrite the integrand of the integral on the r.h.s. as follows:

If we now take the imaginary part of both sides of Eq. (1) and take the limit we find:
we find:

after using the relation:
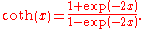
Using that the series expansion of is given by:
is given by:
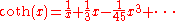
we see that the coefficient of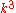 of the series expansion of
of the series expansion of  is
is 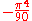 . This then implies that
. This then implies that  and the result
and the result
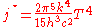
follows.
Thermal Hyper-Conductivity
Metamaterials may be designed to exceed the Stefan–Boltzmann law.
See also
- Wien's displacement lawWien's displacement lawWien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph...
- Rayleigh–Jeans law
- RadianceRadianceRadiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from...
- Zero-dimensional models
- Black bodyBlack bodyA black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
- Sakuma–Hattori equation
-