Black hole thermodynamics
Encyclopedia
In physics
, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics
with the existence of black hole
event horizon
s. Much as the study of the statistical mechanics
of black body
radiation led to the advent of the theory of quantum mechanics
, the effort to understand the statistical mechanics of black holes has had a deep impact upon the understanding of quantum gravity
, leading to the formulation of the holographic principle
.
is to admit that black holes have entropy
. If black holes carried no entropy, it would be possible to violate the second law by throwing mass into the black hole. The increase of the entropy of the black hole more than compensates for the decrease of the entropy carried by the object that was swallowed.
Starting from theorems proved by Stephen Hawking
, Jacob Bekenstein
conjectured that the black hole entropy was proportional to the area of its event horizon
divided by the Planck area. Bekenstein suggested (½ ln 2)/4π as the constant of proportionality, asserting that if the constant was not exactly this, it must be very close to it. The next year, Hawking showed that black holes emit thermal Hawking radiation
corresponding to a certain temperature (Hawking temperature). Using the thermodynamic relationship between energy, temperature and entropy, Hawking was able to confirm Bekenstein's conjecture and fix the constant of proportionality at 1/4:
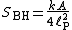
where A is the area of the event horizon, calculated at 4πR2, k is Boltzmann's constant, and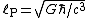
is the Planck length. The subscript BH either stands for "black hole" or "Bekenstein-Hawking". The black hole entropy is proportional to the area of its event horizon 
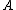. The fact that the black hole entropy is also the maximal entropy that can be obtained by the Bekenstein bound
(wherein the Bekenstein bound becomes an equality) was the main observation that led to the holographic principle
.
Although Hawking's calculations gave further thermodynamic evidence for black hole entropy, until 1995 no one was able to make a controlled calculation of black hole entropy based on statistical mechanics
, which associates entropy with a large number of microstates. In fact, so called "no hair
" theorems appeared to suggest that black holes could have only a single microstate. The situation changed in 1995 when Andrew Strominger
and Cumrun Vafa
calculated the right Bekenstein-Hawking entropy of a supersymmetric
black hole in string theory
, using methods based on D-branes. Their calculation was followed by many similar computations of entropy of large classes of other extremal
and near-extremal black hole
s, and the result always agreed with the Bekenstein-Hawking formula.
Loop quantum gravity
(LQG), viewed as the main competitor of string theory, also offered a calculation of the black hole entropy. This calculation confirms that the entropy is proportional to the surface area, with the proportionality constant dependent on the only free parameter in LQG, Immirzi parameter
.
s are believed to satisfy. The laws, analogous to the laws of thermodynamics
, were discovered by Brandon Carter
, Stephen Hawking
and James Bardeen
.
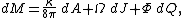
where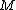
is the mass
,
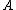is the horizon area, 
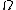is the angular velocity
,
is the angular momentum
,
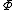is the electrostatic potential, 
is the surface gravity
and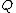
is the electric charge
.
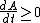
This "law" was superseded by Hawking's discovery that black holes radiate, which causes both the black hole's mass and the area of its horizon to decrease over time.
= 0 is not possible to achieve.
which states that the temperature is constant throughout a body in thermal equilibrium
. It suggests that the surface gravity is analogous to temperature
. T constant for thermal equilibrium for a normal system is analogous to
constant over the horizon of a stationary black hole.
. Analogously, the first law of thermodynamics
is a statement of energy conservation
, which contains on its right hand side the term T dS.
states that the change in entropy
an isolated system will be greater than or equal to 0 for a spontaneous process, suggesting a link between entropy and the area of a black hole horizon. However, this version violates the second law of thermodynamics by matter losing (its) entropy as it falls in, giving a decrease in entropy. Generalized second law introduced as total entropy = black hole entropy + outside entropy.
s have vanishing surface gravity. Stating that
cannot go to zero is analogous to the third law of thermodynamics
which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.
, zero entropy, and the laws of black hole mechanics remain an analogy. However, when quantum mechanical effects
are taken into account, one finds that black holes emit thermal radiation
(Hawking radiation
) at temperature
.
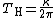From the first law of black hole mechanics, this determines the multiplicative constant of the Bekenstein-Hawking entropy which is
.
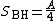More fundamentally, 't Hooft
and Susskind
used the laws of black hole thermodynamics to argue for a general Holographic Principle
of nature, which asserts that consistent theories of gravity and quantum mechanics must be lower dimensional. Though not yet fully understood in general, the holographic principle is central to theories like the AdS/CFT correspondence
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
with the existence of black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
s. Much as the study of the statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
of black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiation led to the advent of the theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the effort to understand the statistical mechanics of black holes has had a deep impact upon the understanding of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, leading to the formulation of the holographic principle
Holographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
.
Black hole entropy
The only way to satisfy the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
is to admit that black holes have entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. If black holes carried no entropy, it would be possible to violate the second law by throwing mass into the black hole. The increase of the entropy of the black hole more than compensates for the decrease of the entropy carried by the object that was swallowed.
Starting from theorems proved by Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
, Jacob Bekenstein
Jacob Bekenstein
Jacob David Bekenstein is an Israeli theoretical physicist who has contributed to the foundation of black hole thermodynamics and to other aspects of the connections between information and gravitation.-Biography:...
conjectured that the black hole entropy was proportional to the area of its event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
divided by the Planck area. Bekenstein suggested (½ ln 2)/4π as the constant of proportionality, asserting that if the constant was not exactly this, it must be very close to it. The next year, Hawking showed that black holes emit thermal Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
corresponding to a certain temperature (Hawking temperature). Using the thermodynamic relationship between energy, temperature and entropy, Hawking was able to confirm Bekenstein's conjecture and fix the constant of proportionality at 1/4:
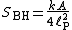
where A is the area of the event horizon, calculated at 4πR2, k is Boltzmann's constant, and
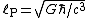is the Planck length. The subscript BH either stands for "black hole" or "Bekenstein-Hawking". The black hole entropy is proportional to the area of its event horizon 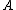. The fact that the black hole entropy is also the maximal entropy that can be obtained by the Bekenstein boundBekenstein bound
In physics, the Bekenstein bound is an upper limit on the entropy S, or information I, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximum amount of information required to perfectly describe a given physical system down to the...
(wherein the Bekenstein bound becomes an equality) was the main observation that led to the holographic principle
Holographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
.
Although Hawking's calculations gave further thermodynamic evidence for black hole entropy, until 1995 no one was able to make a controlled calculation of black hole entropy based on statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, which associates entropy with a large number of microstates. In fact, so called "no hair
No hair theorem
The no-hair theorem postulates that all black hole solutions of the Einstein-Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three externally observable classical parameters: mass, electric charge, and angular momentum...
" theorems appeared to suggest that black holes could have only a single microstate. The situation changed in 1995 when Andrew Strominger
Andrew Strominger
Andrew Eben Strominger is an American theoretical physicist who works on string theory and son of Jack L. Strominger. He is currently a professor at Harvard University and a senior fellow at the Society of Fellows...
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
calculated the right Bekenstein-Hawking entropy of a supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
black hole in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, using methods based on D-branes. Their calculation was followed by many similar computations of entropy of large classes of other extremal
Extremal black hole
In theoretical physics, an extremal black hole is a black hole with the minimal possible mass that can be compatible with a given charge and angular momentum . In other words, this is the smallest possible black hole that can exist while rotating at a given fixed constant speed.The concept of an...
and near-extremal black hole
Near-extremal black hole
In theoretical physics, a near-extremal black hole is a black hole which is not far from the minimal possible mass that can be compatible with the given charges and angular momentum...
s, and the result always agreed with the Bekenstein-Hawking formula.
Loop quantum gravity
Loop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
(LQG), viewed as the main competitor of string theory, also offered a calculation of the black hole entropy. This calculation confirms that the entropy is proportional to the surface area, with the proportionality constant dependent on the only free parameter in LQG, Immirzi parameter
Immirzi parameter
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity, a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units...
.
The laws of black hole mechanics
The four laws of black hole mechanics are physical properties that black holeBlack hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s are believed to satisfy. The laws, analogous to the laws of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, were discovered by Brandon Carter
Brandon Carter
Brandon Carter, FRS is an Australian theoretical physicist, best known for his work on the properties of black holes and for being the first to name and employ the anthropic principle in its contemporary form. He is a researcher at the Meudon campus of the Laboratoire Univers et Théories, part of...
, Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
and James Bardeen
James M. Bardeen
James Maxwell Bardeen is an American physicist, well known for his work in general relativity, particularly his role in formulating the laws of black hole mechanics. He also discovered the Bardeen vacuum, an exact solution of the Einstein field equation.Bardeen graduated from Harvard in 1960 and...
.
Statement of the laws
The laws of black hole mechanics are expressed in geometrized units.The First Law
We have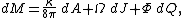where
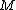is the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
,
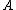is the horizon area, 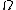is the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
,
is the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
,
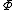is the electrostatic potential, is the surface gravitySurface gravity
The surface gravity, g, of an astronomical or other object is the gravitational acceleration experienced at its surface. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in...
and
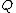is the electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.
The Second Law
The horizon area is, assuming the weak energy condition, a non-decreasing function of time,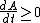This "law" was superseded by Hawking's discovery that black holes radiate, which causes both the black hole's mass and the area of its horizon to decrease over time.
The Third Law
It is not possible to form a black hole with vanishing surface gravity. = 0 is not possible to achieve.The Zeroth Law
The zeroth law is analogous to the zeroth law of thermodynamicsZeroth law of thermodynamics
The zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.Systems are said to...
which states that the temperature is constant throughout a body in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
. It suggests that the surface gravity is analogous to temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. T constant for thermal equilibrium for a normal system is analogous to
constant over the horizon of a stationary black hole.The First Law
The left hand side, dM, is the change in mass/energy. Although the first term does not have an immediately obvious physical interpretation, the second and third terms on the right hand side represent changes in energy due to rotation and electromagnetismElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. Analogously, the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
is a statement of energy conservation
Energy conservation
Energy conservation refers to efforts made to reduce energy consumption. Energy conservation can be achieved through increased efficient energy use, in conjunction with decreased energy consumption and/or reduced consumption from conventional energy sources...
, which contains on its right hand side the term T dS.
The Second Law
The second law is the statement of Hawking's area theorem. Analogously, the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
states that the change in entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
an isolated system will be greater than or equal to 0 for a spontaneous process, suggesting a link between entropy and the area of a black hole horizon. However, this version violates the second law of thermodynamics by matter losing (its) entropy as it falls in, giving a decrease in entropy. Generalized second law introduced as total entropy = black hole entropy + outside entropy.
The Third Law
Extremal black holeExtremal black hole
In theoretical physics, an extremal black hole is a black hole with the minimal possible mass that can be compatible with a given charge and angular momentum . In other words, this is the smallest possible black hole that can exist while rotating at a given fixed constant speed.The concept of an...
s have vanishing surface gravity. Stating that
cannot go to zero is analogous to the third law of thermodynamicsThird law of thermodynamics
The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.
Interpretation of the laws
The four laws of black hole mechanics suggest that one should identify the surface gravity of a black hole with temperature and the area of the event horizon with entropy, at least up to some multiplicative constants. If one only considers black holes classically, then they have zero temperature and, by the no hair theoremNo hair theorem
The no-hair theorem postulates that all black hole solutions of the Einstein-Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three externally observable classical parameters: mass, electric charge, and angular momentum...
, zero entropy, and the laws of black hole mechanics remain an analogy. However, when quantum mechanical effects
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
are taken into account, one finds that black holes emit thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
(Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
) at temperature
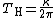.From the first law of black hole mechanics, this determines the multiplicative constant of the Bekenstein-Hawking entropy which is
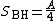.Beyond black holes
Hawking and Page showed that black hole thermodynamics is more general than black holes, that cosmological event horizons also have an entropy and temperature.More fundamentally, 't Hooft
Gerardus 't Hooft
Gerardus 't Hooft is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G...
and Susskind
Leonard Susskind
Leonard Susskind is the Felix Bloch Professor of Theoretical Physics at Stanford University. His research interests include string theory, quantum field theory, quantum statistical mechanics and quantum cosmology...
used the laws of black hole thermodynamics to argue for a general Holographic Principle
Holographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
of nature, which asserts that consistent theories of gravity and quantum mechanics must be lower dimensional. Though not yet fully understood in general, the holographic principle is central to theories like the AdS/CFT correspondence
AdS/CFT correspondence
In physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
.