
Virtual displacement
Encyclopedia
A virtual displacement 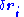 "is an assumed infinitesimal change of system coordinates occurring while time is held constant. It is called virtual rather than real since no actual displacement can take place without the passage of time."
"is an assumed infinitesimal change of system coordinates occurring while time is held constant. It is called virtual rather than real since no actual displacement can take place without the passage of time."
In modern terminology virtual displacement is a tangent vector
to the manifold representing the constraints at a fixed time. Unlike regular displacement which arises from differentiating with respect to time parameter along the path of the motion (thus pointing in the direction of the motion), virtual displacement arises from differentiating with respect to the parameter
along the path of the motion (thus pointing in the direction of the motion), virtual displacement arises from differentiating with respect to the parameter  enumerating paths of the motion variated in a manner consistent with the constraints (thus pointing at a fixed time in the direction tangent to the constraining manifold). The symbol
enumerating paths of the motion variated in a manner consistent with the constraints (thus pointing at a fixed time in the direction tangent to the constraining manifold). The symbol 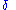 is traditionally used to denote the corresponding derivative
is traditionally used to denote the corresponding derivative  .
.
The total differential of any set of system position vectors, , that are functions of other variables,
, that are functions of other variables, 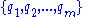 , and time,
, and time,  may be expressed as follows:
may be expressed as follows: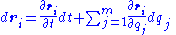
If, instead, we want the virtual displacement (virtual differential displacement), then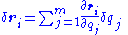
This equation is used in Lagrangian mechanics
to relate generalized coordinates
,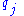 , to virtual work
, to virtual work
, , and generalized forces,
, and generalized forces, 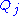 .
.
In analytical mechanics
the concept of a virtual displacement, related to the concept of virtual work
, is meaningful only when discussing a physical system subject to constraints on its motion. A special case of an infinitesimal
displacement (usually notated ), a virtual displacement (notated
), a virtual displacement (notated 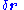 ) refers to an infinitesimal change in the position coordinates of a system such that the constraints remain satisfied.
) refers to an infinitesimal change in the position coordinates of a system such that the constraints remain satisfied.
For example, if a bead is constrained to move on a hoop, its position may be represented by the position coordinate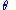 , which gives the angle
, which gives the angle
at which the bead is situated. Say that the bead is at the top. Moving the bead straight upwards from its height to a height
to a height 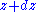 would represent one possible infinitesimal
would represent one possible infinitesimal
displacement
, but would violate the constraint. The only possible virtual displacement would be a displacement from the bead's position, to a new position
to a new position 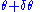 (where
(where 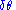 could be positive or negative).
could be positive or negative).
It is also worthwhile to note that virtual displacements are spatial displacements exclusively - time
is fixed while they occur. When computing virtual differentials of quantities that are functions
of space
and time
coordinates, no dependence on time
is considered (formally equivalent to saying ).
).
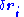 "is an assumed infinitesimal change of system coordinates occurring while time is held constant. It is called virtual rather than real since no actual displacement can take place without the passage of time."
"is an assumed infinitesimal change of system coordinates occurring while time is held constant. It is called virtual rather than real since no actual displacement can take place without the passage of time."In modern terminology virtual displacement is a tangent vector
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to the manifold representing the constraints at a fixed time. Unlike regular displacement which arises from differentiating with respect to time parameter
 along the path of the motion (thus pointing in the direction of the motion), virtual displacement arises from differentiating with respect to the parameter
along the path of the motion (thus pointing in the direction of the motion), virtual displacement arises from differentiating with respect to the parameter  enumerating paths of the motion variated in a manner consistent with the constraints (thus pointing at a fixed time in the direction tangent to the constraining manifold). The symbol
enumerating paths of the motion variated in a manner consistent with the constraints (thus pointing at a fixed time in the direction tangent to the constraining manifold). The symbol 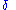 is traditionally used to denote the corresponding derivative
is traditionally used to denote the corresponding derivative  .
.The total differential of any set of system position vectors,
 , that are functions of other variables,
, that are functions of other variables, 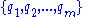 , and time,
, and time,  may be expressed as follows:
may be expressed as follows: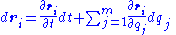
If, instead, we want the virtual displacement (virtual differential displacement), then
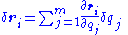
This equation is used in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
to relate generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
,
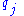 , to virtual work
, to virtual workVirtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
,
 , and generalized forces,
, and generalized forces, 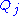 .
.In analytical mechanics
Analytical mechanics
Analytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
the concept of a virtual displacement, related to the concept of virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
, is meaningful only when discussing a physical system subject to constraints on its motion. A special case of an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
displacement (usually notated
 ), a virtual displacement (notated
), a virtual displacement (notated 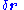 ) refers to an infinitesimal change in the position coordinates of a system such that the constraints remain satisfied.
) refers to an infinitesimal change in the position coordinates of a system such that the constraints remain satisfied.For example, if a bead is constrained to move on a hoop, its position may be represented by the position coordinate
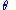 , which gives the angle
, which gives the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
at which the bead is situated. Say that the bead is at the top. Moving the bead straight upwards from its height
 to a height
to a height 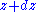 would represent one possible infinitesimal
would represent one possible infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, but would violate the constraint. The only possible virtual displacement would be a displacement from the bead's position,
 to a new position
to a new position 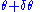 (where
(where 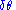 could be positive or negative).
could be positive or negative).It is also worthwhile to note that virtual displacements are spatial displacements exclusively - time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
is fixed while they occur. When computing virtual differentials of quantities that are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
coordinates, no dependence on time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
is considered (formally equivalent to saying
 ).
).

