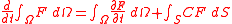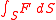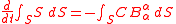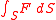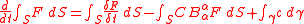Time evolution of integrals
Encyclopedia
In many applications, one needs to calculate the rate of change
of a volume
or surface integral
whose domain of integration
, as well as the integrand, are functions
of a particular parameter. In physical applications, that parameter is frequently time
t.
integrands, is governed by this extension of the fundamental theorem of calculus
:
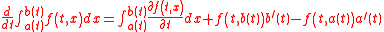
The calculus of moving surfaces provides analogous formulas for volume integrals over Euclidean domains
, and surface integrals over differential geometry of surfaces
, curved surfaces, including integrals over curved surfaces with moving contour boundaries
.
and consider a time-dependent domain Ω with a smooth surface
boundary S. Let F be a time-dependent invariant
field defined in the interior of Ω. Then the rate of change of the integral
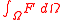
is governed by the following law:
where C is the velocity of the interface. The velocity of the interface C is the fundamental concept in the calculus of moving surfaces. In the above equation, C must be expressed with respect to the exterior normal
. This law can be considered as the generalization of the fundamental theorem of calculus
.
of the surface integral
The law reads
where the -derivative
-derivative
is the fundamental operator in the calculus of moving surfaces, originally proposed by Jacques Hadamard
.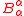 is the trace of the mean curvature tensor. In this law, C need not be expression with respect to the exterior normal, as long as the choice of the normal is consistent for C and
is the trace of the mean curvature tensor. In this law, C need not be expression with respect to the exterior normal, as long as the choice of the normal is consistent for C and 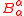 . The first term in the above equation captures the rate of change in F while the second corrects for expanding or shrinking area. The fact that mean curvature represents the rate of change in area follows from applying the above equation to
. The first term in the above equation captures the rate of change in F while the second corrects for expanding or shrinking area. The fact that mean curvature represents the rate of change in area follows from applying the above equation to  since
since 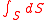 is area:
is area:
The above equation shows that mean curvature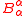 can be appropriately called the shape gradient of area. An evolution governed by
can be appropriately called the shape gradient of area. An evolution governed by
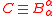
is the popular mean curvature flow
and represents steepest descent with respect to area. Note that for a sphere
of radius R,
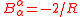 , and for a circle
, and for a circle
of radius R,
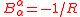
with respect to the exterior normal.
is
The last term captures the change in area due to annexation, as the figure on the right illustrates.
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a volume
Volume integral
In mathematics — in particular, in multivariable calculus — a volume integral refers to an integral over a 3-dimensional domain....
or surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
whose domain of integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, as well as the integrand, are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of a particular parameter. In physical applications, that parameter is frequently time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
t.
Introduction
The rate of change of one dimensional integrals with sufficiently smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
integrands, is governed by this extension of the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
:
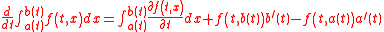
The calculus of moving surfaces provides analogous formulas for volume integrals over Euclidean domains
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, and surface integrals over differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
, curved surfaces, including integrals over curved surfaces with moving contour boundaries
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
.
Volume integrals
Let t be a time-like parameterParameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
and consider a time-dependent domain Ω with a smooth surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
boundary S. Let F be a time-dependent invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
field defined in the interior of Ω. Then the rate of change of the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
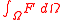
is governed by the following law:
where C is the velocity of the interface. The velocity of the interface C is the fundamental concept in the calculus of moving surfaces. In the above equation, C must be expressed with respect to the exterior normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
. This law can be considered as the generalization of the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
.
Surface integrals
A related law governs the rate of changeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
The law reads
where the
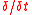 -derivative
-derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is the fundamental operator in the calculus of moving surfaces, originally proposed by Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
.
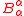 is the trace of the mean curvature tensor. In this law, C need not be expression with respect to the exterior normal, as long as the choice of the normal is consistent for C and
is the trace of the mean curvature tensor. In this law, C need not be expression with respect to the exterior normal, as long as the choice of the normal is consistent for C and 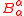 . The first term in the above equation captures the rate of change in F while the second corrects for expanding or shrinking area. The fact that mean curvature represents the rate of change in area follows from applying the above equation to
. The first term in the above equation captures the rate of change in F while the second corrects for expanding or shrinking area. The fact that mean curvature represents the rate of change in area follows from applying the above equation to  since
since 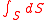 is area:
is area:The above equation shows that mean curvature
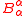 can be appropriately called the shape gradient of area. An evolution governed by
can be appropriately called the shape gradient of area. An evolution governed by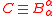
is the popular mean curvature flow
Mean curvature flow
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold . Intuitively, a family of surfaces evolves under mean curvature flow if the velocity of which a point on the surface moves is given by the mean...
and represents steepest descent with respect to area. Note that for a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius R,
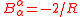 , and for a circle
, and for a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
of radius R,
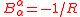
with respect to the exterior normal.
Surface integrals with moving contour boundaries
Suppose that S is a moving surface with a moving contour γ. Suppose that the velocity of the contour γ with respect to S is c. Then the rate of change of the time dependent integral:is
The last term captures the change in area due to annexation, as the figure on the right illustrates.