
Volume element
Encyclopedia
In mathematics
, a volume element provides a means for integrating
a function
with respect to volume
in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form
where the are the coordinates, so that the volume of any set
are the coordinates, so that the volume of any set  can be computed by
can be computed by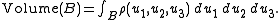
For example, in spherical coordinates , and so
, and so  .
.
The notion of a volume element is not limited to three-dimensions: in two-dimensions it is often known as the area element, and in this setting it is useful for doing surface integral
s. Under changes of coordinates, the volume element changes by the absolute value of the Jacobian determinant of the coordinate transformation (by the change of variables formula). This fact allows volume elements to be defined as a kind of measure
on a manifold
. On an orientable
differentiable manifold
, a volume element typically arises from a volume form
: a top degree differential form
. On a non-orientable manifold, the volume element is typically the absolute value
of a (locally defined) volume form: it defines a 1-density
.
of the n-dimensional Euclidean space
Rn that is spanned by a collection of linearly independent vectors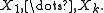
To find the volume element of the subspace, it is useful to know the fact from linear algebra that the volume of the parallelepiped spanned by the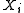 is the square root of the determinant
is the square root of the determinant
of the Gramian matrix of the :
: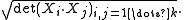
Any point p in the subspace can be given coordinates such that
such that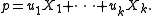
At a point p, if we form a small parallelepiped with sides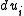 , then the volume of that parallelepiped is the square root of the determinant of the Grammian matrix
, then the volume of that parallelepiped is the square root of the determinant of the Grammian matrix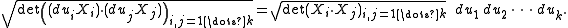
This therefore defines the volume form in the linear subspace.
embedded in n-dimensional Euclidean space
. Consider a subset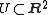 and a mapping function
and a mapping function
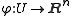
thus defining a surface embedded in . In two dimensions, volume is just area, and a volume element gives a way to determine the area of parts of the surface. Thus a volume element is an expression of the form
. In two dimensions, volume is just area, and a volume element gives a way to determine the area of parts of the surface. Thus a volume element is an expression of the form
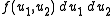
that allows one to compute the area of a set B lying on the surface by computing the integral
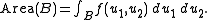
Here we will find the volume element on the surface that defines area in the usual sense. The Jacobian matrix of the mapping is
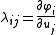
with index i running from 1 to n, and j running from 1 to 2. The Euclidean metric
in the n-dimensional space induces a metric on the set U, with matrix elements
on the set U, with matrix elements
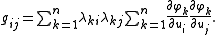
The determinant
of the metric is given by
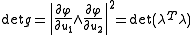
For a regular surface, this determinant is non-vanishing; equivalently, the Jacobian matrix has rank 2.
Now consider a change of coordinates on U, given by a diffeomorphism

so that the coordinates are given in terms of
are given in terms of  by
by  . The Jacobian matrix of this transformation is given by
. The Jacobian matrix of this transformation is given by
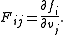
In the new coordinates, we have
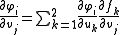
and so the metric transforms as

where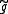 is the pullback metric in the v coordinate system. The determinant is
is the pullback metric in the v coordinate system. The determinant is
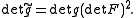
Given the above construction, it should now be straightforward to understand how the volume element is invariant under an orientation-preserving change of coordinates.
In two dimensions, the volume is just the area. The area of a subset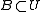 is given by the integral
is given by the integral
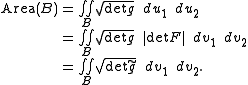
Thus, in either coordinate system, the volume element takes the same expression: the expression of the volume element is invariant under a change of coordinates.
Note that there was nothing particular to two dimensions in the above presentation; the above trivially generalizes to arbitrary dimensions.

Then
and the volume element is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a volume element provides a means for integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with respect to volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form

where the
 are the coordinates, so that the volume of any set
are the coordinates, so that the volume of any set  can be computed by
can be computed by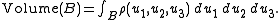
For example, in spherical coordinates
 , and so
, and so  .
.The notion of a volume element is not limited to three-dimensions: in two-dimensions it is often known as the area element, and in this setting it is useful for doing surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
s. Under changes of coordinates, the volume element changes by the absolute value of the Jacobian determinant of the coordinate transformation (by the change of variables formula). This fact allows volume elements to be defined as a kind of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. On an orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, a volume element typically arises from a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
: a top degree differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
. On a non-orientable manifold, the volume element is typically the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a (locally defined) volume form: it defines a 1-density
Density on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
.
Volume element of a linear subspace
Consider the linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn that is spanned by a collection of linearly independent vectors
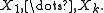
To find the volume element of the subspace, it is useful to know the fact from linear algebra that the volume of the parallelepiped spanned by the
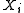 is the square root of the determinant
is the square root of the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Gramian matrix of the
 :
: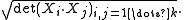
Any point p in the subspace can be given coordinates
 such that
such that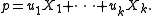
At a point p, if we form a small parallelepiped with sides
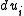 , then the volume of that parallelepiped is the square root of the determinant of the Grammian matrix
, then the volume of that parallelepiped is the square root of the determinant of the Grammian matrix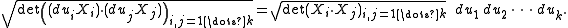
This therefore defines the volume form in the linear subspace.
Volume element of a surface
A simple example of a volume element can be explored by considering a two-dimensional surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
embedded in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Consider a subset
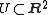 and a mapping function
and a mapping function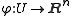
thus defining a surface embedded in
 . In two dimensions, volume is just area, and a volume element gives a way to determine the area of parts of the surface. Thus a volume element is an expression of the form
. In two dimensions, volume is just area, and a volume element gives a way to determine the area of parts of the surface. Thus a volume element is an expression of the form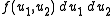
that allows one to compute the area of a set B lying on the surface by computing the integral
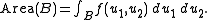
Here we will find the volume element on the surface that defines area in the usual sense. The Jacobian matrix of the mapping is
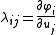
with index i running from 1 to n, and j running from 1 to 2. The Euclidean metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
in the n-dimensional space induces a metric
 on the set U, with matrix elements
on the set U, with matrix elements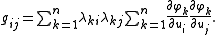
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric is given by
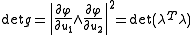
For a regular surface, this determinant is non-vanishing; equivalently, the Jacobian matrix has rank 2.
Now consider a change of coordinates on U, given by a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

so that the coordinates
 are given in terms of
are given in terms of  by
by  . The Jacobian matrix of this transformation is given by
. The Jacobian matrix of this transformation is given by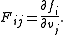
In the new coordinates, we have
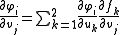
and so the metric transforms as

where
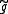 is the pullback metric in the v coordinate system. The determinant is
is the pullback metric in the v coordinate system. The determinant is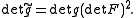
Given the above construction, it should now be straightforward to understand how the volume element is invariant under an orientation-preserving change of coordinates.
In two dimensions, the volume is just the area. The area of a subset
 is given by the integral
is given by the integral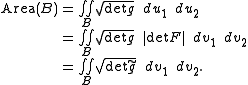
Thus, in either coordinate system, the volume element takes the same expression: the expression of the volume element is invariant under a change of coordinates.
Note that there was nothing particular to two dimensions in the above presentation; the above trivially generalizes to arbitrary dimensions.
Example: Sphere
For example, consider the sphere with radius r centered at the origin in R3. This can be parametrized using spherical coordinates with the map
Then

and the volume element is

See also
- Cylindrical coordinate system#Line and volume elements
- Spherical coordinate system#Integration and differentiation in spherical coordinates

