Density on a manifold
Encyclopedia
In mathematics
, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold
which can be integrated
in an intrinsic manner. Abstractly, a density is a section
of a certain trivial
line bundle
, called the density bundle. An element of the density bundle at x is a function that assigns a volume for the parallelotope
spanned by the n given tangent vectors at x.
From the operational point of view, a density is a collection of functions on coordinate charts which become multiplied by the absolute value of the Jacobian determinant in the change of coordinates. Densities can be generalized into s-densities, whose coordinate representations become multiplied by the s-th power of the absolute value. On an oriented manifold 1-densities can be canonically identified with the n-forms
on M. On non-orientable manifolds this identification cannot be made, since the density bundle is the tensor product of the orientation bundle of M and the n-th exterior product bundle of T*M (see pseudotensor
.)
that assigns a volume for any such parallelotype, it should satisfy the following properties:
If any linear combination of the vectors v1,...,vj-1,vj+1,...,vn is added to the vector vj, the volume should stay invariant.
These conditions are equivalent to the statement that μ is given by a translation-invariant measure on V, and they can be rephrased as
Any such mapping is called a density on the vector space V. The set Vol(V) of all densities on V forms a one-dimensional vector space, and any n-form ω on V defines a density |ω| on V by
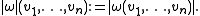
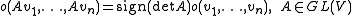
forms a one-dimensional vector space, and an orientation on V is one of the two elements o∈Or(V) such that |o(v1,...,vn)|=1 for any linearly independent v1,...,vn. Any non-zero n-form ω on V defines an orientation o∈Or(V) such that
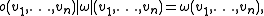
and vice versa, any o∈Or(V) and any density μ∈Vol(V) define an n-form ω on V by
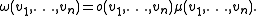
In terms of tensor product spaces
,
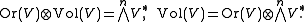
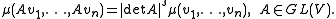
Just like densities, s-densities form a one-dimensional vector space Vols(V), and any n-form ω on V defines an s-density |ω|s on V by
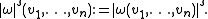
The product of s1- and s2-densities μ1 and μ2 form an (s1+s2)-density μ by
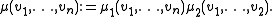
In terms of tensor product spaces
this fact can be stated as
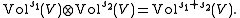
construction, intertwining the one-dimensional group representation
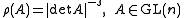
of the general linear group
with the frame bundle
of M. More precisely,
The resulting line bundle is known as the bundle of s-densities, and is denoted by
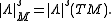
A 1-density is also referred to simply as a density.
More generally, the associated bundle construction also allows densities to be constructed from any vector bundle
E on M.
In detail, if (Uα,φα) is an atlas
of coordinate charts on M, then there is associated a local trivialization of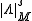
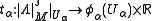
subordinate to the open cover Uα such that the associated GL(1)-cocycle
satisfies
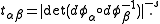
on manifolds. Indeed, the definition of a density is motivated by how a measure dx changes under a change of coordinates .
Given a 1-density ƒ supported in a coordinate chart Uα, the integral is defined by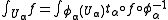
where the latter integral is with respect to the Lebesgue measure
on Rn. The transformation law for 1-densities together with the Jacobian change of variables
ensures compatibility on the overlaps of different coordinate charts, and so the integral of a general compactly supported 1-density can be defined by a partition of unity argument. Thus 1-densities are a generalization of the notion of a volume form that does not necessarily require the manifold to be oriented or even orientable. One can more generally develop a general theory of Radon measure
s as distributional
sections of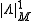
using the Riesz representation theorem
.
The set of 1/p-densities such that
is a normed linear space whose completion 
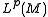is called the intrinsic Lp space
of M.
, a different weighting convention is used: the bundle of s-densities is instead associated with the character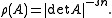
With this convention, for instance, one integrates n-densities (rather than 1-densities). Also in these conventions, a conformal metric is identified with a tensor density
of weight 2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
which can be integrated
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
in an intrinsic manner. Abstractly, a density is a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of a certain trivial
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
, called the density bundle. An element of the density bundle at x is a function that assigns a volume for the parallelotope
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
spanned by the n given tangent vectors at x.
From the operational point of view, a density is a collection of functions on coordinate charts which become multiplied by the absolute value of the Jacobian determinant in the change of coordinates. Densities can be generalized into s-densities, whose coordinate representations become multiplied by the s-th power of the absolute value. On an oriented manifold 1-densities can be canonically identified with the n-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on M. On non-orientable manifolds this identification cannot be made, since the density bundle is the tensor product of the orientation bundle of M and the n-th exterior product bundle of T*M (see pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
.)
Motivation (Densities in vector spaces)
In general, there does not exist a natural concept of a "volume" for a parallelotype generated by vectors v1,...,vn in a n-dimensional vector space V. However, if one wishes to define a functionthat assigns a volume for any such parallelotype, it should satisfy the following properties:
- If any of the vectors
These conditions are equivalent to the statement that μ is given by a translation-invariant measure on V, and they can be rephrased as
Any such mapping is called a density on the vector space V. The set Vol(V) of all densities on V forms a one-dimensional vector space, and any n-form ω on V defines a density |ω| on V by
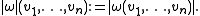
Orientations on a vector space
The set Or(V) of all functions that satisfy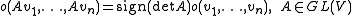forms a one-dimensional vector space, and an orientation on V is one of the two elements o∈Or(V) such that |o(v1,...,vn)|=1 for any linearly independent v1,...,vn. Any non-zero n-form ω on V defines an orientation o∈Or(V) such that
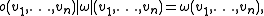
and vice versa, any o∈Or(V) and any density μ∈Vol(V) define an n-form ω on V by
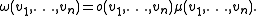
In terms of tensor product spaces
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
,
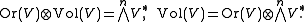
s-densities on a vector space
The s-densities on V are functions such that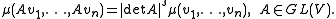Just like densities, s-densities form a one-dimensional vector space Vols(V), and any n-form ω on V defines an s-density |ω|s on V by
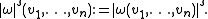
The product of s1- and s2-densities μ1 and μ2 form an (s1+s2)-density μ by
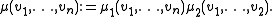
In terms of tensor product spaces
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
this fact can be stated as
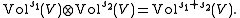
Definition
Formally, the s-density bundle Vols(M) of a differentiable manifold M is obtained by an associated bundleAssociated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
construction, intertwining the one-dimensional group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
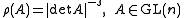
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
with the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of M. More precisely,
The resulting line bundle is known as the bundle of s-densities, and is denoted by
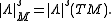
A 1-density is also referred to simply as a density.
More generally, the associated bundle construction also allows densities to be constructed from any vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
E on M.
In detail, if (Uα,φα) is an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
of coordinate charts on M, then there is associated a local trivialization of
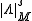
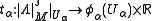
subordinate to the open cover Uα such that the associated GL(1)-cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
satisfies
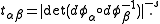
Integration
Densities play a significant role in the theory of integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
on manifolds. Indeed, the definition of a density is motivated by how a measure dx changes under a change of coordinates .
Given a 1-density ƒ supported in a coordinate chart Uα, the integral is defined by
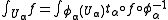
where the latter integral is with respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on Rn. The transformation law for 1-densities together with the Jacobian change of variables
Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
ensures compatibility on the overlaps of different coordinate charts, and so the integral of a general compactly supported 1-density can be defined by a partition of unity argument. Thus 1-densities are a generalization of the notion of a volume form that does not necessarily require the manifold to be oriented or even orientable. One can more generally develop a general theory of Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s as distributional
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
sections of
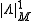using the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
.
The set of 1/p-densities such that
is a normed linear space whose completion 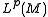is called the intrinsic Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of M.
Conventions
In some areas, particularly conformal geometryConformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
, a different weighting convention is used: the bundle of s-densities is instead associated with the character
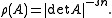
With this convention, for instance, one integrates n-densities (rather than 1-densities). Also in these conventions, a conformal metric is identified with a tensor density
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
of weight 2.
Properties
- The dual vector bundle of
is 
. - Tensor densitiesTensor densityIn differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
are sections of the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of a density bundle with a tensor bundle.