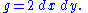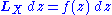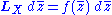
Conformal geometry
Encyclopedia
In mathematics
, conformal geometry is the study of the set of angle-preserving (conformal
) transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces. In more than two dimensions, conformal geometry may refer either to the study of conformal transformations of "flat" spaces (such as Euclidean space
s or spheres), or, more commonly, to the study of conformal manifolds which are Riemannian
or pseudo-Riemannian manifold
s with a class of metrics
defined up to scale. Study of the flat structures is sometimes termed Möbius geometry, and is a type of Klein geometry
.
equipped with an equivalence class of (pseudo-)Riemannian metric tensor
s, in which two metrics g and h are equivalent (see also: Conformal equivalence
) if and only if
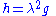
where λ > 0 is a smooth positive function. An equivalence class of such metrics is known as a conformal metric or conformal class. Thus a conformal metric may be regarded as a metric that is only defined "up to scale". Often conformal metrics are treated by selecting a metric in the conformal class, and applying only "conformally invariant" constructions to the chosen metric.
A conformal metric is conformally flat if there is a metric representing it that is flat, in the usual sense that the Riemann tensor vanishes. It may only be possible to find a metric in the conformal class that is flat in an open neighborhood of each point. When it is necessary to distinguish these cases, the latter is called locally conformally flat, although often in the literature no distinction is maintained. The n-sphere is a locally conformally flat manifold that is not globally conformally flat in this sense, whereas a Euclidean space, a torus, or any conformal manifold that is covered by an open subset of Euclidean space is (globally) conformally flat in this sense. A locally conformally flat manifold is locally conformal to a Möbius geometry meaning that there exists an angle preserving local diffeomorphism
from the manifold into a Möbius geometry. In two dimensions, every conformal metric is locally conformally flat. In dimension n > 3 a conformal metric is locally conformally flat if and only if its Weyl tensor
vanishes; in dimension n = 3, if and only if the Cotton tensor
vanishes.
Conformal geometry has a number of features which distinguish it from (pseudo-)Riemannian geometry. The first is that although in (pseudo-)Riemannian geometry one has a well-defined metric at each point, in conformal geometry one only has a class of metrics. Thus the length of a tangent vector
cannot be defined, but the angle between two vectors still can. Another feature is that there is no Levi-Civita connection
because if g and λ2g are two representatives of the conformal structure, then the Christoffel symbols of g and λ2g would not agree. Those associated with λ2g would involve derivatives of the function λ whereas those associated with g would not.
Despite these differences, conformal geometry is still tractable. The Levi-Civita connection and curvature tensor
, although only being defined once a particular representative of the conformal structure has been singled out, do satisfy certain transformation laws involving the λ and its derivatives when a different representative is chosen. In particular, (in dimension higher than 3) the Weyl tensor
turns out not to depend on λ, and so it is a conformal invariant. Moreover, even though there is no Levi-Civita connection on a conformal manifold, one can instead work with a conformal connection
, which can be handled either as a type of Cartan connection
modelled on the associated Möbius geometry, or as a Weyl connection. This allows one to define conformal curvature, as well as other invariants of the conformal structure.
with a point added at infinity", or a "Minkowski (or pseudo-Euclidean) space
with a null cone added at infinity". That is, the setting is a compactification
of a familiar space; the geometry
is concerned with the implications of preserving angles.
At an abstract level, the Euclidean and pseudo-Euclidean spaces can be handled in much the same way, except in the case of dimension two. The compactified two dimensional Minkowski plane exhibits extensive conformal symmetry
. Formally, its group of conformal transformations is infinite dimensional. By contrast, the group of conformal transformations of the compactified Euclidean plane is only 6 dimensional.
Lie group
:
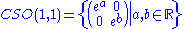
with Lie algebra
cso(1, 1) consisting of all real diagonal 2 × 2 matrices.
Consider now the Minkowski plane: R2 equipped with the metric
A 1-parameter group of conformal transformations gives rise to a vector field X with the property that the Lie derivative of g along X is proportional to g. Symbolically,
In particular, using the above description of the Lie algebra cso(1, 1), this implies that
for some real-valued functions a and b depending, respectively, on x and y. Conversely, given any such pair of real-valued functions, there exists a vector field X satisfying 1. and 2. Hence the Lie algebra
of infinitesimal symmetries of the conformal structure is infinite dimensional.
The conformal compactification of the Minkowski plane is a Cartesian product of two circles S1 × S1. On the universal cover, there is no obstruction to integrating the infinitesimal symmetries, and so the group of conformal transformations is the infinite dimensional Lie group
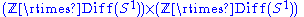
where Diff(S1) is the diffeomorphism group of the circle.
The conformal group CSO(1, 1) and its Lie algebra are of current interest in conformal field theory
. See also Virasoro algebra
.
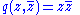
is the group GL1(C) = C* of non-zero complex numbers. Its Lie algebra is gl1(C) = C.
Consider the (Euclidean) complex plane
equipped with the metric
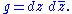
The infinitesimal conformal symmetries satisfy
where ƒ satisfies the Cauchy-Riemann equation, and so is holomorphic over its domain. (See Witt algebra
.)
The conformal isometries of a domain therefore consist of holomorphic self-maps. In particular, on the conformal compactification — the Riemann sphere
— the conformal transformations are given by the Möbius transformations
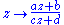
where ad − bc is nonzero.
In the case of higher dimensions, the asymptotic developments of infinitesimal symmetries are at most quadratic polynomials. In particular, they form a finite dimensional Lie algebra. The pointwise infinitesimal conformal symmetries of a manifold can be integrated precisely when the manifold is a certain model conformally flat space (up to
taking universal covers and discrete group quotients).
The general theory of conformal geometry is similar, although with some differences, in the cases of Euclidean and pseudo-Euclidean signature. In either case, there are a number of ways of introducing the model space of conformally flat geometry. Unless otherwise clear from the context, this article treats the case of Euclidean conformal geometry with the understanding that it also applies, mutatis mutandis
, to the pseudo-Euclidean situation.
En generated by inversion in spheres. By Liouville's theorem, any angle-preserving local (conformal) transformation is of this form. From this perspective, the transformation properties of flat conformal space are those of inversive geometry.
in a projective space
. Let q denote the Lorentzian quadratic form
on Rn+2 defined by
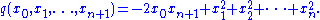
In the projective space P(Rn+2), let S be the locus of q = 0. Then S is the projective (or Möbius) model of conformal geometry. A conformal transformation on S is a projective linear transformation
of P(Rn+2) which preserves the quadric.
In a related construction, the quadric S is thought of as the celestial sphere
at infinity of the null cone in the Minkowski space Rn+1, 1, which is equipped with the quadratic form q as above. The null cone is defined by
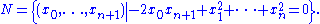
This is the affine cone over the projective quadric S. Let N+ be the future part of the null cone (with the origin deleted). Then the tautological projection Rn+1, 1 − {0} → P(Rn+2) restricts to a projection N+ → S. This gives N+ the structure of a line bundle
over S. Conformal transformations on S are induced by the orthochronous Lorentz transformation
s of Rn+1, 1, since these are homogeneous linear transformations preserving the future null cone.
of a sphere. Conformal symmetries of a sphere are generated by the inversion in all of its hyperspheres. On the other hand, Riemannian isometries
of a sphere are generated by inversions in geodesic
hyperspheres (see the Cartan-Dieudonné theorem
.) The Euclidean sphere can be mapped to the conformal sphere in a canonical manner, but not vice-versa.
The Euclidean unit sphere is the locus in Rn+1

This can be mapped to the Minkowski space Rn+1,1 by letting
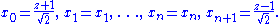
It is readily seen that the image of the sphere under this transformation is null in the Minkowski space, and so it lies on the cone N+. Consequently, it determines a cross-section of the line bundle N+ → S.
Nevertheless, there was an arbitrary choice. In fact, if κ(x) is any positive function of x=(z, x0, ..., xn), then the assignment
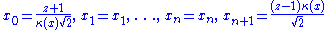
also gives a mapping into N+. The function κ is an arbitrary choice of conformal scale.
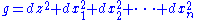
to the sphere

A conformal representative of g is a metric of the form λ²g where λ is a positive function on the sphere. The conformal class of g, denoted [g], is the collection of all such representatives:
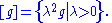
An embedding of the Euclidean sphere into N+, as in the previous section, determines a conformal scale on S. Conversely, any conformal scale on S is given by such an embedding. Thus the line bundle N+ → S is identified with the bundle of conformal scales on S: to give a section of this bundle is tantamount to specifying a metric in the conformal class [g].
on Rn+1, 1. Suppose that the Euclidean n-sphere S carries a stereographic coordinate system
. This consists of the following map of Rn → S ⊂ Rn+1:
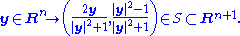
In terms of these stereographic coordinates, it is possible to give a coordinate system on the null cone N+ in Minkowski space. Using the embedding given above, the representative metric section of the null cone is
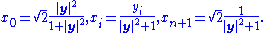
Introduce a new variable t corresponding to dilations up N+, so that the null cone is coordinatized by
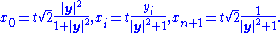
Finally, let ρ be the following defining function of N+:
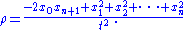
In the t, ρ, y coordinates on Rn+1,1, the Minkowski metric takes the form:
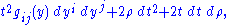
where gij is the metric on the sphere.
In these terms, a section of the bundle N+ consists of a specification of the value of the variable t = t(yi) as a function of the yi along the null cone ρ = 0. This yields the following representative of the conformal metric on S:
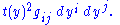
of the (n + 2)-dimensional Lorentzian space Rn+1,1. Here the model is a Klein geometry
: a homogeneous space
G/H where G = SO(n + 1, 1) acting on the (n+2)-dimensional Lorentzian space Rn+1,1 and H is the isotropy group of a fixed null ray in the light cone
. Thus the conformally flat models are the spaces of inversive geometry. For pseudo-Euclidean of metric signature
(p, q), the model flat geometry is defined analogously as the homogeneous space O(p + 1, q + 1)/H, where H is again taken as the stabilizer of a null line. Note that both the Euclidean and pseudo-Euclidean model spaces are compact
.
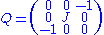
where J is a quadratic form of signature (p, q). Then G = O(p + 1, q + 1) consists of (n + 2) × (n + 2) matrices stabilizing Q: tMQM = Q. The Lie algebra admits a Cartan decomposition
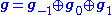
where
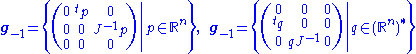
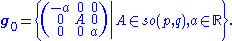
Alternatively, this decomposition agrees with a natural Lie algebra structure defined on Rn ⊕ cso(p, q) ⊕ (Rn)*.
The stabilizer of the null ray pointing up the last coordinate vector is given by the Borel subalgebra
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, conformal geometry is the study of the set of angle-preserving (conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
) transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces. In more than two dimensions, conformal geometry may refer either to the study of conformal transformations of "flat" spaces (such as Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s or spheres), or, more commonly, to the study of conformal manifolds which are Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s with a class of metrics
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
defined up to scale. Study of the flat structures is sometimes termed Möbius geometry, and is a type of Klein geometry
Klein geometry
In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry.For background and motivation...
.
Conformal manifolds
A conformal manifold is a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
equipped with an equivalence class of (pseudo-)Riemannian metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
s, in which two metrics g and h are equivalent (see also: Conformal equivalence
Conformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
) if and only if
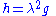
where λ > 0 is a smooth positive function. An equivalence class of such metrics is known as a conformal metric or conformal class. Thus a conformal metric may be regarded as a metric that is only defined "up to scale". Often conformal metrics are treated by selecting a metric in the conformal class, and applying only "conformally invariant" constructions to the chosen metric.
A conformal metric is conformally flat if there is a metric representing it that is flat, in the usual sense that the Riemann tensor vanishes. It may only be possible to find a metric in the conformal class that is flat in an open neighborhood of each point. When it is necessary to distinguish these cases, the latter is called locally conformally flat, although often in the literature no distinction is maintained. The n-sphere is a locally conformally flat manifold that is not globally conformally flat in this sense, whereas a Euclidean space, a torus, or any conformal manifold that is covered by an open subset of Euclidean space is (globally) conformally flat in this sense. A locally conformally flat manifold is locally conformal to a Möbius geometry meaning that there exists an angle preserving local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
from the manifold into a Möbius geometry. In two dimensions, every conformal metric is locally conformally flat. In dimension n > 3 a conformal metric is locally conformally flat if and only if its Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
vanishes; in dimension n = 3, if and only if the Cotton tensor
Cotton tensor
In differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...
vanishes.
Conformal geometry has a number of features which distinguish it from (pseudo-)Riemannian geometry. The first is that although in (pseudo-)Riemannian geometry one has a well-defined metric at each point, in conformal geometry one only has a class of metrics. Thus the length of a tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
cannot be defined, but the angle between two vectors still can. Another feature is that there is no Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
because if g and λ2g are two representatives of the conformal structure, then the Christoffel symbols of g and λ2g would not agree. Those associated with λ2g would involve derivatives of the function λ whereas those associated with g would not.
Despite these differences, conformal geometry is still tractable. The Levi-Civita connection and curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
, although only being defined once a particular representative of the conformal structure has been singled out, do satisfy certain transformation laws involving the λ and its derivatives when a different representative is chosen. In particular, (in dimension higher than 3) the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
turns out not to depend on λ, and so it is a conformal invariant. Moreover, even though there is no Levi-Civita connection on a conformal manifold, one can instead work with a conformal connection
Conformal connection
In conformal differential geometry, a conformal connection is a Cartan connection on an n-dimensional manifold M arising as a deformation of the Klein geometry given by the celestial n-sphere, viewed as the homogeneous space...
, which can be handled either as a type of Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
modelled on the associated Möbius geometry, or as a Weyl connection. This allows one to define conformal curvature, as well as other invariants of the conformal structure.
Möbius geometry
Möbius geometry is the study of "Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with a point added at infinity", or a "Minkowski (or pseudo-Euclidean) space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
with a null cone added at infinity". That is, the setting is a compactification
Compactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
of a familiar space; the geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
is concerned with the implications of preserving angles.
At an abstract level, the Euclidean and pseudo-Euclidean spaces can be handled in much the same way, except in the case of dimension two. The compactified two dimensional Minkowski plane exhibits extensive conformal symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Formally, its group of conformal transformations is infinite dimensional. By contrast, the group of conformal transformations of the compactified Euclidean plane is only 6 dimensional.
Minkowski space
The conformal group for the Minkowski quadratic form q(x, y) = 2xy in the plane is the abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
:
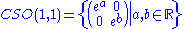
with Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
cso(1, 1) consisting of all real diagonal 2 × 2 matrices.
Consider now the Minkowski plane: R2 equipped with the metric
A 1-parameter group of conformal transformations gives rise to a vector field X with the property that the Lie derivative of g along X is proportional to g. Symbolically,
- LX g = λ g for some λ.
In particular, using the above description of the Lie algebra cso(1, 1), this implies that
- LX dx = a(x) dx
- LX dy = b(y) dy
for some real-valued functions a and b depending, respectively, on x and y. Conversely, given any such pair of real-valued functions, there exists a vector field X satisfying 1. and 2. Hence the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of infinitesimal symmetries of the conformal structure is infinite dimensional.
The conformal compactification of the Minkowski plane is a Cartesian product of two circles S1 × S1. On the universal cover, there is no obstruction to integrating the infinitesimal symmetries, and so the group of conformal transformations is the infinite dimensional Lie group
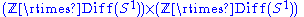
where Diff(S1) is the diffeomorphism group of the circle.
The conformal group CSO(1, 1) and its Lie algebra are of current interest in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. See also Virasoro algebra
Virasoro algebra
In mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
.
Euclidean space
The group of conformal symmetries of the quadratic form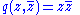
is the group GL1(C) = C* of non-zero complex numbers. Its Lie algebra is gl1(C) = C.
Consider the (Euclidean) complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
equipped with the metric
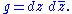
The infinitesimal conformal symmetries satisfy
where ƒ satisfies the Cauchy-Riemann equation, and so is holomorphic over its domain. (See Witt algebra
Witt algebra
In mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie...
.)
The conformal isometries of a domain therefore consist of holomorphic self-maps. In particular, on the conformal compactification — the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
— the conformal transformations are given by the Möbius transformations
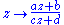
where ad − bc is nonzero.
Higher dimensions
In two dimensions, the group of conformal automorphisms of a space can be quite large (as in the case of Lorentzian signature) or variable (as with the case of Euclidean signature). The comparative lack of rigidity of the two-dimensional case with that of higher dimensions owes to the analytical fact that the asymptotic developments of the infinitesimal automorphisms of the structure are relatively unconstrained. In Lorentzian signature, the freedom is in a pair of real valued functions. In Euclidean, the freedom is in a single holomorphic function.In the case of higher dimensions, the asymptotic developments of infinitesimal symmetries are at most quadratic polynomials. In particular, they form a finite dimensional Lie algebra. The pointwise infinitesimal conformal symmetries of a manifold can be integrated precisely when the manifold is a certain model conformally flat space (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
taking universal covers and discrete group quotients).
The general theory of conformal geometry is similar, although with some differences, in the cases of Euclidean and pseudo-Euclidean signature. In either case, there are a number of ways of introducing the model space of conformally flat geometry. Unless otherwise clear from the context, this article treats the case of Euclidean conformal geometry with the understanding that it also applies, mutatis mutandis
Mutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
, to the pseudo-Euclidean situation.
The inversive model
The inversive model of conformal geometry consists of the group of local transformations on the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
En generated by inversion in spheres. By Liouville's theorem, any angle-preserving local (conformal) transformation is of this form. From this perspective, the transformation properties of flat conformal space are those of inversive geometry.
The projective model
The projective model identifies the conformal sphere with a certain quadricQuadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
in a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Let q denote the Lorentzian quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on Rn+2 defined by
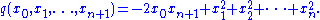
In the projective space P(Rn+2), let S be the locus of q = 0. Then S is the projective (or Möbius) model of conformal geometry. A conformal transformation on S is a projective linear transformation
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
of P(Rn+2) which preserves the quadric.
In a related construction, the quadric S is thought of as the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
at infinity of the null cone in the Minkowski space Rn+1, 1, which is equipped with the quadratic form q as above. The null cone is defined by
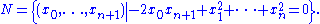
This is the affine cone over the projective quadric S. Let N+ be the future part of the null cone (with the origin deleted). Then the tautological projection Rn+1, 1 − {0} → P(Rn+2) restricts to a projection N+ → S. This gives N+ the structure of a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
over S. Conformal transformations on S are induced by the orthochronous Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s of Rn+1, 1, since these are homogeneous linear transformations preserving the future null cone.
The Euclidean sphere
Intuitively, the conformally flat geometry of a sphere is less rigid than the Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
of a sphere. Conformal symmetries of a sphere are generated by the inversion in all of its hyperspheres. On the other hand, Riemannian isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of a sphere are generated by inversions in geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
hyperspheres (see the Cartan-Dieudonné theorem
Cartan-Dieudonné theorem
In mathematics, the Cartan–Dieudonné theorem, named after Élie Cartan and Jean Dieudonné, is a theorem on the structure of the automorphism group of symmetric bilinear spaces.-Statement of the theorem:...
.) The Euclidean sphere can be mapped to the conformal sphere in a canonical manner, but not vice-versa.
The Euclidean unit sphere is the locus in Rn+1

This can be mapped to the Minkowski space Rn+1,1 by letting
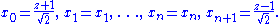
It is readily seen that the image of the sphere under this transformation is null in the Minkowski space, and so it lies on the cone N+. Consequently, it determines a cross-section of the line bundle N+ → S.
Nevertheless, there was an arbitrary choice. In fact, if κ(x) is any positive function of x=(z, x0, ..., xn), then the assignment
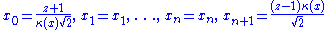
also gives a mapping into N+. The function κ is an arbitrary choice of conformal scale.
Representative metrics
A representative Riemannian metric on the sphere is a metric which is proportional to the standard sphere metric. This gives a realization of the sphere as a conformal manifold. The standard sphere metric is the restriction of the Euclidean metric on Rn+1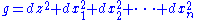
to the sphere

A conformal representative of g is a metric of the form λ²g where λ is a positive function on the sphere. The conformal class of g, denoted [g], is the collection of all such representatives:
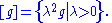
An embedding of the Euclidean sphere into N+, as in the previous section, determines a conformal scale on S. Conversely, any conformal scale on S is given by such an embedding. Thus the line bundle N+ → S is identified with the bundle of conformal scales on S: to give a section of this bundle is tantamount to specifying a metric in the conformal class [g].
Ambient metric model
Another way to realize the representative metrics is through a special coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
on Rn+1, 1. Suppose that the Euclidean n-sphere S carries a stereographic coordinate system
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. This consists of the following map of Rn → S ⊂ Rn+1:
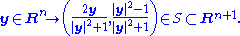
In terms of these stereographic coordinates, it is possible to give a coordinate system on the null cone N+ in Minkowski space. Using the embedding given above, the representative metric section of the null cone is
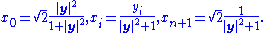
Introduce a new variable t corresponding to dilations up N+, so that the null cone is coordinatized by
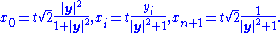
Finally, let ρ be the following defining function of N+:
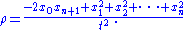
In the t, ρ, y coordinates on Rn+1,1, the Minkowski metric takes the form:
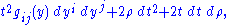
where gij is the metric on the sphere.
In these terms, a section of the bundle N+ consists of a specification of the value of the variable t = t(yi) as a function of the yi along the null cone ρ = 0. This yields the following representative of the conformal metric on S:
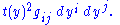
The Kleinian model
Consider first the case of the flat conformal geometry in Euclidean signature. The n-dimensional model is the celestial sphereCelestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
of the (n + 2)-dimensional Lorentzian space Rn+1,1. Here the model is a Klein geometry
Klein geometry
In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry.For background and motivation...
: a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
G/H where G = SO(n + 1, 1) acting on the (n+2)-dimensional Lorentzian space Rn+1,1 and H is the isotropy group of a fixed null ray in the light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
. Thus the conformally flat models are the spaces of inversive geometry. For pseudo-Euclidean of metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(p, q), the model flat geometry is defined analogously as the homogeneous space O(p + 1, q + 1)/H, where H is again taken as the stabilizer of a null line. Note that both the Euclidean and pseudo-Euclidean model spaces are compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
The conformal Lie algebras
To describe the groups and algebras involved in the flat model space, fix the following form on Rp+1,q+1: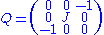
where J is a quadratic form of signature (p, q). Then G = O(p + 1, q + 1) consists of (n + 2) × (n + 2) matrices stabilizing Q: tMQM = Q. The Lie algebra admits a Cartan decomposition
Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
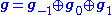
where
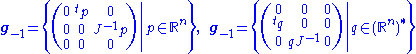
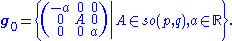
Alternatively, this decomposition agrees with a natural Lie algebra structure defined on Rn ⊕ cso(p, q) ⊕ (Rn)*.
The stabilizer of the null ray pointing up the last coordinate vector is given by the Borel subalgebra
- h = g0 ⊕ g1.
External links
- http://www.euclideanspace.com/maths/geometry/space/nonEuclid/conformal/index.htm