
Virasoro algebra
Encyclopedia
In mathematics
, the Virasoro algebra (named after the physicist Miguel Angel Virasoro
) is a complex Lie algebra
, given as a central extension
of the complex polynomial vector fields on the circle
, and is widely used in conformal field theory
and string theory
.
by elements
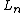 for
for 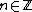
and c with
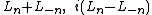
and c being real elements. Here the central element c is the central charge
. The algebra satisfies
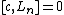
and
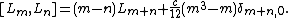
The factor of 1/12 is merely a matter of convention.
The Virasoro algebra is a central extension of the
(complex) Witt algebra
of complex polynomial vector fields on the circle. The Lie algebra of real polynomial vector fields on the circle is a dense subalgebra of the Lie algebra of diffeomorphisms of the circle.
The Virasoro algebra is obeyed by the stress tensor
in string theory
, since it comprises the generators of the conformal group of the worldsheet
, obeys the commutation relations of (two copies of) the Virasoro algebra. This is because the conformal group decomposes into separate diffeomorphisms of the forward and back lightcones. Diffeomorphism invariance of the worldsheet implies additionally that the stress tensor vanishes. This is known as the Virasoro constraint, and in the quantum theory
, cannot be applied to all the states in the theory, but rather only on the physical states (compare Gupta-Bleuler quantization).
 that is killed by
that is killed by 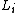 for
for 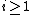 , and is an eigenvector of
, and is an eigenvector of 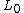 and
and  . The letters
. The letters 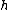 and
and  are usually used for the eigenvalues of
are usually used for the eigenvalues of 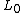 and
and  on
on  . (The same letter
. (The same letter  is used for both the element
is used for both the element  of the Virasoro algebra and its eigenvalue.) For every pair of complex numbers
of the Virasoro algebra and its eigenvalue.) For every pair of complex numbers 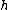 and
and  there is a unique irreducible lowest weight representation with these eigenvalues.
there is a unique irreducible lowest weight representation with these eigenvalues.
A lowest weight representation is called unitary if it has a positive definite inner product such that
the adjoint of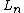 is
is  .
.
The irreducible lowest weight representation with eigenvalues h and c is unitary if and only if either c≥1 and h≥0, or c is one of the values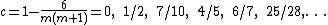
for m = 2, 3, 4, .... and h is one of the values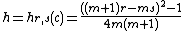
for r = 1, 2, 3, ..., m−1 and s= 1, 2, 3, ..., r.
Daniel Friedan
, Zongan Qiu, and Stephen Shenker
(1984) showed that these conditions are necessary, and Peter Goddard, Adrian Kent and David Olive
(1986) used the coset construction
or GKO construction (identifying unitary representations of the Virasoro algebra within tensor products of unitary representations of affine Kac-Moody algebras) to show that they are sufficient. The unitary irreducible lowest weight representations with c < 1 are called the discrete series representations of the Virasoro algebra. These are special cases of the representations with m = q/(p−q), 0<r<q, 0< s<p for p and q coprime integers and r and s integers, called the minimal models and first studied in Belavin et al. (1984).
The first few discrete series representations are given by:
The lowest weight representations that are not irreducible can be read off from the Kac determinant formula,
which states that the determinant of the invariant inner product on the degree h+N piece of the lowest weight module with eigenvalues c and h is given by
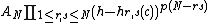
which was stated by V. Kac (1978), (see also Kac and Raina 1987) and whose first published proof was given by Feigin and Fuks (1984). (The function p(N) is the partition function, and AN is some constant.) The reducible highest weight representations are the representations with h and c given in terms of m, c, and h by the formulas above, except that m is not restricted to be an integer ≥ 2 and may be any number other than 0 and 1, and r and s may be any positive integers. This result was used by Feigin and Fuks to find the characters of all irreducible lowest weight representations.
.
The Virasoro algebra is a central extension of the Lie algebra of meromorphic vector fields on a genus 0 Riemann surface that are holomorphic except at two fixed points.
I.V. Krichever and S.P. Novikov (1987) found a central extension of the Lie algebra of meromorphic vector fields on a higher genus compact Riemann surface that are holomorphic except at two fixed points, and M. Schlichenmaier (1993) extended this to the case of more than two points.
The Virasoro algebra also has vertex algebraic
and conformal algebraic
counterparts, which basically come from arranging all the basis elements into generating series and working with single objects. Unsurprisingly these are called the vertex Virasoro and conformal Virasoro algebras respectively.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Virasoro algebra (named after the physicist Miguel Angel Virasoro
Miguel Angel Virasoro
Miguel Angel Virasoro is an Argentine physicist who did most of his work in Italy. The Virasoro algebra is named after him. Together with Giorgio Parisi and Marc Mezard he discovered the...
) is a complex Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, given as a central extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the complex polynomial vector fields on the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, and is widely used in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
Definition
The Virasoro algebra is spannedLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by elements
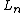 for
for 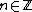
and c with
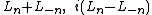
and c being real elements. Here the central element c is the central charge
Central charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
. The algebra satisfies
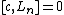
and
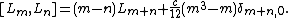
The factor of 1/12 is merely a matter of convention.
The Virasoro algebra is a central extension of the
(complex) Witt algebra
Witt algebra
In mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie...
of complex polynomial vector fields on the circle. The Lie algebra of real polynomial vector fields on the circle is a dense subalgebra of the Lie algebra of diffeomorphisms of the circle.
The Virasoro algebra is obeyed by the stress tensor
Stress tensor
Stress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, since it comprises the generators of the conformal group of the worldsheet
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
, obeys the commutation relations of (two copies of) the Virasoro algebra. This is because the conformal group decomposes into separate diffeomorphisms of the forward and back lightcones. Diffeomorphism invariance of the worldsheet implies additionally that the stress tensor vanishes. This is known as the Virasoro constraint, and in the quantum theory
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, cannot be applied to all the states in the theory, but rather only on the physical states (compare Gupta-Bleuler quantization).
Representation theory
A lowest weight representation of the Virasoro algebra is a representation generated by a vector that is killed by
that is killed by 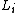 for
for 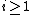 , and is an eigenvector of
, and is an eigenvector of 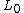 and
and  . The letters
. The letters 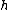 and
and  are usually used for the eigenvalues of
are usually used for the eigenvalues of 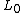 and
and  on
on  . (The same letter
. (The same letter  is used for both the element
is used for both the element  of the Virasoro algebra and its eigenvalue.) For every pair of complex numbers
of the Virasoro algebra and its eigenvalue.) For every pair of complex numbers 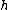 and
and  there is a unique irreducible lowest weight representation with these eigenvalues.
there is a unique irreducible lowest weight representation with these eigenvalues.A lowest weight representation is called unitary if it has a positive definite inner product such that
the adjoint of
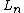 is
is  .
.The irreducible lowest weight representation with eigenvalues h and c is unitary if and only if either c≥1 and h≥0, or c is one of the values
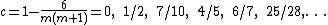
for m = 2, 3, 4, .... and h is one of the values
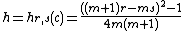
for r = 1, 2, 3, ..., m−1 and s= 1, 2, 3, ..., r.
Daniel Friedan
Daniel Friedan
Daniel Harry Friedan is an American theoretical physicist and is one of two sons of the feminist author and activist Betty Friedan. He earned his Ph.D...
, Zongan Qiu, and Stephen Shenker
Stephen Shenker
Stephen Hart Shenker is an American theoretical physicist who works on string theory. He is a professor at Stanford University and former director of the Stanford Institute for Theoretical Physics. His brother Scott Shenker is a computer scientist...
(1984) showed that these conditions are necessary, and Peter Goddard, Adrian Kent and David Olive
David Olive
David Olive CBE FLSW FRS, is a British theoretical physicist. Olive made fundamental contributions to the string theory and duality theory. He was Professor of physics at Imperial College, London...
(1986) used the coset construction
Coset construction
In mathematics, the coset construction is a method of constructing unitary highest weight representations of the Virasoro algebra, introduced by Peter Goddard, Adrian Kent and David Olive...
or GKO construction (identifying unitary representations of the Virasoro algebra within tensor products of unitary representations of affine Kac-Moody algebras) to show that they are sufficient. The unitary irreducible lowest weight representations with c < 1 are called the discrete series representations of the Virasoro algebra. These are special cases of the representations with m = q/(p−q), 0<r<q, 0< s<p for p and q coprime integers and r and s integers, called the minimal models and first studied in Belavin et al. (1984).
The first few discrete series representations are given by:
- m = 2: c = 0, h = 0. The trivial representation.
- m = 3: c = 1/2, h = 0, 1/16, 1/2. These 3 representations are related to the Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
- m = 4: c = 7/10. h = 0, 3/80, 1/10, 7/16, 3/5, 3/2. These 6 representations are related to the tri critical Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. - m = 5: c = 4/5. There are 10 representations, which are related to the 3-state Potts modelPotts modelIn statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
. - m = 6: c = 6/7. There are 15 representations, which are related to the tri critical 3-state Potts modelPotts modelIn statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
.
The lowest weight representations that are not irreducible can be read off from the Kac determinant formula,
which states that the determinant of the invariant inner product on the degree h+N piece of the lowest weight module with eigenvalues c and h is given by
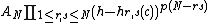
which was stated by V. Kac (1978), (see also Kac and Raina 1987) and whose first published proof was given by Feigin and Fuks (1984). (The function p(N) is the partition function, and AN is some constant.) The reducible highest weight representations are the representations with h and c given in terms of m, c, and h by the formulas above, except that m is not restricted to be an integer ≥ 2 and may be any number other than 0 and 1, and r and s may be any positive integers. This result was used by Feigin and Fuks to find the characters of all irreducible lowest weight representations.
Generalizations
There are two supersymmetric N=1 extensions of the Virasoro algebra, called the Neveu-Schwarz algebra and the Ramond algebra. Their theory is similar to that of the Virasoro algebra. There are further extensions of these algebras with more supersymmetry, such as the N = 2 superconformal algebraN = 2 superconformal algebra
In mathematical physics, the N = 2 superconformal algebra is an infinite-dimensional Lie superalgebra, related to supersymmetry, that occurs in string theory and conformal field theory. It has important applications in mirror symmetry...
.
The Virasoro algebra is a central extension of the Lie algebra of meromorphic vector fields on a genus 0 Riemann surface that are holomorphic except at two fixed points.
I.V. Krichever and S.P. Novikov (1987) found a central extension of the Lie algebra of meromorphic vector fields on a higher genus compact Riemann surface that are holomorphic except at two fixed points, and M. Schlichenmaier (1993) extended this to the case of more than two points.
The Virasoro algebra also has vertex algebraic
Vertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
and conformal algebraic
Lie conformal algebra
A Lie conformal algebra is in some sense a generalization of a Lie algebra in the sense that it too is a "Lie algebra," though a in different pseudo-tensor category...
counterparts, which basically come from arranging all the basis elements into generating series and working with single objects. Unsurprisingly these are called the vertex Virasoro and conformal Virasoro algebras respectively.
History
The Witt algebra (the Virasoro algebra without the central extension) was discovered by E. Cartan (1909). Its analogues over finite fields were studied by E. Witt in about the 1930s. The central extension of the Witt algebra that gives the Virasoro algebra was first found (in characteristic p>0) by R. E. Block (1966, page 381) and independently rediscovered (in characteristic 0) by I. M. Gelfand and D. B. Fuchs (1968). Virasoro (1970) wrote down some operators generating the Virasoso algebra while studying dual resonance models, though he did not find the central extension. The central extension giving the Virasoro algebra was rediscovered in physics shortly after by J. H. Weis, according to Brower and Thorn (1971, footnote on page 167).See also
- Witt algebraWitt algebraIn mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie...
- WZW model
- conformal field theoryConformal field theoryA conformal field theory is a quantum field theory that is invariant under conformal transformations...
- No-ghost theorem
- Lie conformal algebraLie conformal algebraA Lie conformal algebra is in some sense a generalization of a Lie algebra in the sense that it too is a "Lie algebra," though a in different pseudo-tensor category...

