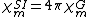Gaussian units
Encyclopedia
Metric system
The metric system is an international decimalised system of measurement. France was first to adopt a metric system, in 1799, and a metric system is now the official system of measurement, used in almost every country in the world...
of physical units
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
. This system is the most common of the several electromagnetic unit systems based on cgs (centimetre-gram-second) units
Centimetre gram second system of units
The centimetre–gram–second system is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time...
. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units. The term "cgs units" is ambiguous and therefore to be avoided if possible: cgs contains within it several conflicting sets of electromagnetism units, not just Gaussian units, as described below.
The most common alternative to Gaussian units are SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
. SI units are predominant in most fields, and continue to increase in popularity at the expense of Gaussian units. (Other alternative unit systems also exist, as discussed below.) Conversions between Gaussian units and SI units are not as simple as normal unit conversions. For example, the formulas for physical laws of electromagnetism (such as Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
) need to be adjusted depending on what system of units one uses. As another example, quantities that are unitless in one system may have dimensions in another.
Alternative unit systems
The main alternative to the Gaussian unit system is SI unitsInternational System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
, historically also called the MKS system of units
Mks system of units
The MKS system of units is a physical system of units that expresses any given measurement using fundamental units of the metre, kilogram, and/or second ....
for metres-kilogram-seconds.
The Gaussian unit system is just one of several electromagnetic unit systems within CGS. Others include "electrostatic units", "electromagnetic units", and Lorentz–Heaviside units.
Some other unit systems are called "natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
", a category that includes atomic units
Atomic units
Atomic units form a system of natural units which is especially convenient for atomic physics calculations. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article...
, Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
, and others. These are closer to CGS units than to SI units in some respects.
SI units are by far the most common today. In engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and practical areas, SI is near-universal and has been for decades, while in technical, scientific literature (such as theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
), Gaussian units were predominant until recent decades, but are now getting progressively less so.
Natural units are most common in more theoretical and abstract fields of physics, particularly particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
"Rationalized" unit systems
One difference between Gaussian and SI units is in the factors of 4π in various formulas. SI is called "rationalized", because Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
have no explicit factors of 4π in the formulas. On the other hand, the force laws, Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
and the Biot–Savart law, do have factors of 4π in them. In Gaussian units, which are not "rationalized", the situation is reversed: Two of Maxwell's equations have factors of 4π in the formulas, while both of the force laws, Coulomb's law and the Biot–Savart law, have no factors of 4π.
Unit of charge
A major difference between Gaussian and SI units is in the definition of the unit of charge. In SI, a separate base unit (the ampereAmpere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
) is associated with electrical phenomena, with the consequence that something like electrical charge (1 coulomb=1 ampere × 1 second) cannot be expressed purely in terms of the mechanical units (kilogram, metre, second). On the other hand, in Gaussian units, the unit of electrical charge (the statcoulomb
Statcoulomb
The statcoulomb or franklin or electrostatic unit of charge is the physical unit for electrical charge used in the centimetre-gram-second system of units and Gaussian units. It is a derived unit given by...
, statC) can be written entirely as a dimensional combination of the mechanical units (gram, centimetre, second), as:
- 1 statC = 1 g1/2 cm3/2 s−1
For example, Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
in cgs units is particularly simple:
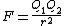
where F is the repulsive force between two electrical charges, Q1 and Q2 are the two charges in question, and r is the distance separating them. If Q1 and Q2 are expressed in statC and r in cm
Centimetre
A centimetre is a unit of length in the metric system, equal to one hundredth of a metre, which is the SI base unit of length. Centi is the SI prefix for a factor of . Hence a centimetre can be written as or — meaning or respectively...
, then F will come out expressed in dyne
Dyne
In physics, the dyne is a unit of force specified in the centimetre-gram-second system of units, a predecessor of the modern SI. One dyne is equal to exactly 10 µN...
.
By contrast, the same law in SI units is:
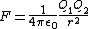
where ε0 is the vacuum permitivity, a quantity with dimensions, namely A2 s4 kg−1 m−3. Without ε0, the two sides could not have consistent dimensions in SI, and in fact the quantity ε0 does not even exist in Gaussian units.
Units for magnetism
In Gaussian units, unlike SI units, the electric field E and the magnetic field BMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
have the same dimension. This amounts to a factor of c
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
difference between how B is defined in the two unit systems, on top of the other differences. (The same factor applies to other magnetic quantities such as H
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and M
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
.) For example, in a planar light wave in vacuum
Sinusoidal plane-wave solutions of the electromagnetic wave equation
Sinusoidal plane-wave solutions are particular solutions to the electromagnetic wave equation.The general solution of the electromagnetic wave equation in homogeneous, linear, time-independent media can be written as a linear superposition of plane-waves of different frequencies and...
, |E(r,t)|=|B(r,t)| in Gaussian units, while |E(r,t)|=c|B(r,t)| in SI units.
Polarization, magnetization
There are further differences between Gaussian and SI units in how quantities related to polarization and magnetization are defined. For one thing, in Gaussian units, all of the following quantities have the same dimension: EElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, D, P
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
, B, H
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, and M
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
. Another important point is that the electric
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
and magnetic susceptibility
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
of a material is dimensionless in both Gaussian and SI units, but a given material will have a different numerical susceptibility in the two systems. (Equation is given below.)
List of equations
This section has a list of the basic formulae of electromagnetism, given in both Gaussian and SI units. Most symbol names are not given; for complete explanations and definitions, please click to the appropriate dedicated article for each equation. All formulas except otherwise noted are from Ref.Maxwell's equations
Here are Maxwell's equations, both in macroscopic and microscopic forms. Only the "differential form" of the equations is given, not the "integral form"; to get the integral forms apply the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
or Kelvin–Stokes theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.
| Name | Gaussian units | SI units |
|---|---|---|
| Gauss's law Gauss's law In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:... (macroscopic) |
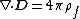 |
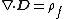 |
| Gauss's law Gauss's law In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:... (microscopic) |
 |
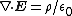 |
| Gauss's law for magnetism: | 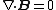 |
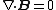 |
| Maxwell–Faraday equation (Faraday's law of induction Faraday's law of induction Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators... ): |
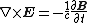 |
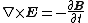 |
| Ampère–Maxwell equation (macroscopic): |
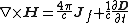 |
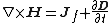 |
| Ampère–Maxwell equation (microscopic): |
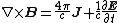 |
 |
Other basic laws
| Name | Gaussian units | SI units |
|---|---|---|
| Lorentz force Lorentz force In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:... |
 |
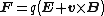 |
| Coulomb's law Coulomb's law Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism... |
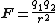 |
 |
| Electric field of stationary point charge Coulomb's law Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism... |
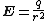 |
 |
| Biot–Savart law | 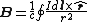 |
 |
Dielectric and magnetic materials
Below are the expressions for the various fields in a dielectric medium. It is assumed here for simplicity that the medium is homogeneous, linear, isotropic, and nondispersive, so that the permittivityPermittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
is a simple constant.
| Gaussian units | SI units |
|---|---|
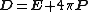 |
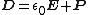 |
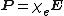 |
 |
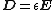 |
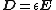 |
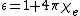 |
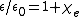 |
where
- E and D are the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and displacement field, respectively; - P is the polarization densityPolarization densityIn classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
;  is the permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
is the permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
;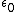 is the permittivity of vacuum (used in the SI system, but meaningless in Gaussian units);
is the permittivity of vacuum (used in the SI system, but meaningless in Gaussian units);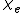 is the electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
is the electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
The quantities
 in Gaussian units and
in Gaussian units and 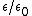 in SI are both dimensionless, and they have the same numeric value. By contrast, the electric susceptibility
in SI are both dimensionless, and they have the same numeric value. By contrast, the electric susceptibilityElectric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
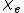 is unitless in both systems, but has different numeric values in the two systems for the same material:
is unitless in both systems, but has different numeric values in the two systems for the same material:
Next, here are the expressions for the various fields in a magnetic medium. Again, it is assumed that the medium is homogeneous, linear, isotropic, and nondispersive, so that the permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
is a simple constant.
| Gaussian units | SI units |
|---|---|
 |
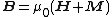 |
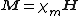 |
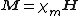 |
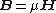 |
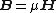 |
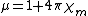 |
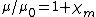 |
where
- B and H are the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s - M is magnetizationMagnetizationIn classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
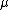 is magnetic permeability
is magnetic permeability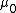 is the permeability of vacuum (used in the SI system, but meaningless in Gaussian units);
is the permeability of vacuum (used in the SI system, but meaningless in Gaussian units);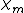 is the magnetic susceptibilityMagnetic susceptibilityIn electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
is the magnetic susceptibilityMagnetic susceptibilityIn electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
The quantities
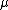 in Gaussian units and
in Gaussian units and 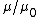 in SI are both dimensionless, and they have the same numeric value. By contrast, the magnetic susceptibility
in SI are both dimensionless, and they have the same numeric value. By contrast, the magnetic susceptibilityMagnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
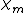 is unitless in both systems, but has different numeric values in the two systems for the same material:
is unitless in both systems, but has different numeric values in the two systems for the same material:
Vector and scalar potentials
The electric and magnetic fields can be written in terms of a vector potential A and a scalar potential φ:| Name | Gaussian units | SI units |
|---|---|---|
| Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... (static) |
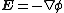 |
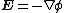 |
| Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... (general) |
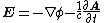 |
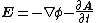 |
| Magnetic B field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
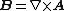 |
 |
Electromagnetic unit names
(For non-electromagnetic units, see main cgs articleCentimetre gram second system of units
The centimetre–gram–second system is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time...
.)
| Quantity | Symbol | SI unit | Gaussian unit |
|---|---|---|---|
| electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... |
q | 1 C | ↔ (10−1 c) Fr Statcoulomb The statcoulomb or franklin or electrostatic unit of charge is the physical unit for electrical charge used in the centimetre-gram-second system of units and Gaussian units. It is a derived unit given by... |
| electric current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... |
I | 1 A Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... |
↔ (10−1 c) Fr Statcoulomb The statcoulomb or franklin or electrostatic unit of charge is the physical unit for electrical charge used in the centimetre-gram-second system of units and Gaussian units. It is a derived unit given by... ·s−1 |
| electric potential Electric potential In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there... voltage Voltage Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points... |
φ V |
1 V Volt The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the... |
↔ (108 c−1) statV Statvolt The statvolt is a unit of voltage and electrical potential used in the cgs system of units. The conversion to the SI system isIt is a useful unit for electromagnetism because one statvolt per centimetre is equal in magnitude to one gauss. Thus, for example, an electric field of one statvolt/cm has... |
| electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... |
E | 1 V Volt The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the... /m Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... |
↔ (106 c−1) statV Statvolt The statvolt is a unit of voltage and electrical potential used in the cgs system of units. The conversion to the SI system isIt is a useful unit for electromagnetism because one statvolt per centimetre is equal in magnitude to one gauss. Thus, for example, an electric field of one statvolt/cm has... /cm Centimetre A centimetre is a unit of length in the metric system, equal to one hundredth of a metre, which is the SI base unit of length. Centi is the SI prefix for a factor of . Hence a centimetre can be written as or — meaning or respectively... |
| magnetic induction Magnetic induction Magnetic induction may refer to one of the following:* Electromagnetic induction* Magnetic field B is sometimes called magnetic induction... |
B | 1 T Tesla (unit) The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla... |
↔ (104) G Gauss (unit) The gauss, abbreviated as G, is the cgs unit of measurement of a magnetic field B , named after the German mathematician and physicist Carl Friedrich Gauss. One gauss is defined as one maxwell per square centimeter; it equals 1 tesla... |
| magnetic field strength | H | 1 A Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... /m Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... |
↔ (4π 10−3) Oe Oersted Oersted is the unit of magnetizing field in the CGS system of units.-Difference between cgs and SI systems:... |
| magnetic dipole moment | μ | 1 A Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... ·m² Square metre The square metre or square meter is the SI derived unit of area, with symbol m2 . It is defined as the area of a square whose sides measure exactly one metre... |
↔ (103) erg Erg An erg is the unit of energy and mechanical work in the centimetre-gram-second system of units, symbol "erg". Its name is derived from the Greek ergon, meaning "work".... /G Gauss (unit) The gauss, abbreviated as G, is the cgs unit of measurement of a magnetic field B , named after the German mathematician and physicist Carl Friedrich Gauss. One gauss is defined as one maxwell per square centimeter; it equals 1 tesla... |
| magnetic flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... |
Φm | 1 Wb Weber (unit) In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :... |
↔ (108) G Gauss (unit) The gauss, abbreviated as G, is the cgs unit of measurement of a magnetic field B , named after the German mathematician and physicist Carl Friedrich Gauss. One gauss is defined as one maxwell per square centimeter; it equals 1 tesla... ·cm² |
| resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical... |
R | 1 Ω Ohm The ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,... |
↔ (109 c−2) s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... /cm Centimetre A centimetre is a unit of length in the metric system, equal to one hundredth of a metre, which is the SI base unit of length. Centi is the SI prefix for a factor of . Hence a centimetre can be written as or — meaning or respectively... |
| resistivity | ρ | 1 Ω Ohm The ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,... ·m Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... |
↔ (1011 c−2) s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
| capacitance Capacitance In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor... |
C | 1 F Farad The farad is the SI unit of capacitance. The unit is named after the English physicist Michael Faraday.- Definition :A farad is the charge in coulombs which a capacitor will accept for the potential across it to change 1 volt. A coulomb is 1 ampere second... |
↔ (10−9 c2) cm Centimetre A centimetre is a unit of length in the metric system, equal to one hundredth of a metre, which is the SI base unit of length. Centi is the SI prefix for a factor of . Hence a centimetre can be written as or — meaning or respectively... |
| inductance Inductance In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit... |
L | 1 H | ↔ (109 c−2) s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... 2·cm Centimetre A centimetre is a unit of length in the metric system, equal to one hundredth of a metre, which is the SI base unit of length. Centi is the SI prefix for a factor of . Hence a centimetre can be written as or — meaning or respectively... −1 |
In this table, the letter c represents the number 29,979,245,800 ≈ 3·1010, the numerical value of the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
expressed in cm/s. The symbol "↔" was used instead of "=" as a reminder that the SI and Gaussian units are corresponding but not equal because they have incompatible dimensions. For example, according to the top row of the table, something with a charge of 1 C also has a charge of (10−1 c) Fr
Statcoulomb
The statcoulomb or franklin or electrostatic unit of charge is the physical unit for electrical charge used in the centimetre-gram-second system of units and Gaussian units. It is a derived unit given by...
, but it is usually incorrect to replace "1 C" with "(10−1 c) Fr" within an equation or formula.
It is surprising to think of measuring capacitance in centimetres. One useful example is that a centimetre of capacitance is the capacitance between a sphere of radius 1 cm in vacuum and infinity.
Another surprising unit is measuring resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
in units of seconds. A physical example is: Take a parallel-plate capacitor, which has a "leaky" dielectric with permittivity 1 but a finite resistivity. After charging it up, the capacitor will discharge itself over time, due to current leaking through the dielectric. If the resistivity of the dielectric is "X" seconds, the half-life of the discharge is ~0.05X seconds. This result is independent of the size, shape, and charge of the capacitor, and therefore this example illuminates the fundamental connection between resistivity and time-units.
Dimensionally-equivalent units
A number of the units defined by the table have different names but are in fact dimensionally equivalent—i.e., the have the same expression in terms of the base units cm, g, s. (This is analogous to the distinction in SI between becquerelBecquerel
The becquerel is the SI-derived unit of radioactivity. One Bq is defined as the activity of a quantity of radioactive material in which one nucleus decays per second. The Bq unit is therefore equivalent to an inverse second, s−1...
and Hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
, or between Newton metre
Newton metre
A newton metre is a unit of torque in the SI system. The symbolic form is N m or N·m, and sometimes hyphenated newton-metre...
and Joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
.) The different names help avoid ambiguities and misunderstandings as to what physical quantity is being measured. In particular, all of the following quantities are dimensionally equivalent in Gaussian units, but they are nevertheless given different unit names as follows:
| Quantity | In Gaussian base units |
Gaussian unit of measure |
|---|---|---|
| E Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... |
cm-1/2 g1/2 s−1 | statV/cm |
| D | cm-1/2 g1/2 s−1 | statC/cm2 |
| P Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... |
cm-1/2 g1/2 s−1 | statC/cm2 |
| B Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
cm-1/2 g1/2 s−1 | G Gauss (unit) The gauss, abbreviated as G, is the cgs unit of measurement of a magnetic field B , named after the German mathematician and physicist Carl Friedrich Gauss. One gauss is defined as one maxwell per square centimeter; it equals 1 tesla... |
| H Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
cm-1/2 g1/2 s−1 | Oe Oersted Oersted is the unit of magnetizing field in the CGS system of units.-Difference between cgs and SI systems:... |
| M Magnetization In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material... |
cm-1/2 g1/2 s−1 | Mx Maxwell (unit) The maxwell, abbreviated as Mx, is the compound derived CGS unit of magnetic flux. The unit was previously called a line. The unit name honours James Clerk Maxwell, who presented the unified theory of electromagnetism, and was established by the IEC in 1930.In a magnetic field of strength one... /cm2 or emu/cm3 |
General rules to translate a formula
To convert any formula from Gaussian units to SI units, replace the quantity in the Gaussian column by the quantity in the SI column (vice-versa to convert the other way). This will reproduce any of the specific formulas given in the list above, such as Maxwell's equations, as well as any other formula not listed. It may also be necessary to use the relation to simplify. For some examples of how to use this table, see:
to simplify. For some examples of how to use this table, see:| Name | Gaussian units | SI units |
|---|---|---|
| Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... , Electric potential Electric potential In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there... |
 |
 |
| Electric displacement field | 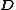 |
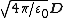 |
| Charge Charge (physics) In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:... , Charge density Charge density The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as... , Current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... , Current density Current density Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved... , Polarization density Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... , Electric dipole moment Electric dipole moment In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter... |
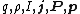 |
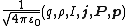 |
| Magnetic B field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... , Magnetic flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... , Magnetic vector potential |
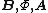 |
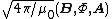 |
| Magnetic H field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
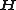 |
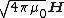 |
| Magnetic moment Magnetic moment The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it... , Magnetization Magnetization In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material... |
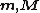 |
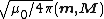 |
| Relative permittivity, Relative permeability Permeability (electromagnetism) In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically... |
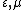 |
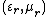 , or equivalently, , or equivalently,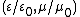 |
| Electric susceptibility Electric susceptibility In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field... , Magnetic susceptibility Magnetic susceptibility In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field... |
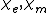 |
 |
| Conductivity, Conductance, Capacitance Capacitance In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor... |
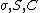 |
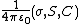 |
| Resistivity Resistivity Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre... , Resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical... , Inductance Inductance In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit... |
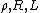 |
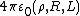 |