Electric displacement field
Encyclopedia
In physics
, the electric displacement field, denoted as
, is a vector field
that appears in Maxwell's equations
.
It accounts for the effects of free
charges
within materials. "D" stands for "displacement," as in the related concept of displacement current
in dielectric
s. In free space, the electric displacement field is equivalent to flux density
, a concept that lends understanding to Gauss's law
.
material the presence of an electric field
E causes the bound charges in the material (atomic nuclei
and their electron
s) to slightly separate, inducing a local
electric dipole moment
. The electric displacement field D is defined as
where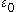
is the vacuum permittivity (also called permittivity of free space),
and P is the (macroscopic) density of the permanent and induced electric dipole moments in the material, called the polarization density
. Separating the total volume charge density into free and bound charges:
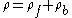
the density can be rewritten as a function of the polarization P:
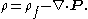
P is a vector field whose divergence
yields the density of bound charges
in the material. The electric field satisfies the equation:
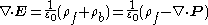
and hence
.
The displacement field therefore satisfies Gauss's law
in a dielectric:
.
D is not determined exclusively by the free charge. Consider the relationship:
Which, by the fact that E has a curl of zero in electrostatic situations, evaluates to:
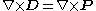
Which can be immediately seen in the case of some object with a "frozen in" polarization like a bar electret
, the electric analogue to a bar magnet. There is no free charge in such a material, but the inherent polarization gives rise to an electric field. If the wayward student were to assume the D field were entirely determined by the free charge, he or she would immediately conclude the electric field were zero in such a material, but this is patently not true. The electric field can be properly determined by using the above relation along with other boundary conditions on the polarization density
yielding the bound charges, which will, in turn, yield the electric field.
In a linear
, homogeneous
, isotropic dielectric with instantaneous response to changes in the electric field, P depends linearly on the electric field,
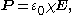
where the constant of proportionality
is called the electric susceptibility
of the material. Thus
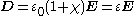
where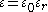
is the permittivity
, and
the relative permittivity
of the material.
In linear, homogeneous, isotropic media
is a constant. However, in linear anisotropic media it is a matrix
, and in
nonhomogeneous media it is a function of position inside the medium. It may also depend upon the electric field (nonlinear materials) and have a time dependent response. Explicit time dependence can arise if the materials are physically moving or changing in time (e.g. reflections off a moving interface give rise to Doppler shifts). A different form of time dependence can arise in a time-invariant medium, in that there can be a time delay between the imposition of the electric field and the resulting polarization of the material. In this case, P is a convolution
of the impulse response
susceptibility χ and the electric field E. Such a convolution takes on a simpler form in the frequency domain
—by Fourier transform
ing the relationship and applying the convolution theorem
, one obtains the following relation for a linear time-invariant medium:
where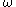
is frequency of the applied field (e.g. in radian/s). The constraint of causality
leads to the Kramers–Kronig relations, which place limitations upon the form of the frequency dependence. The phenomenon of a frequency-dependent permittivity is an example of material dispersion
. In fact, all physical materials have some material dispersion because they cannot respond instantaneously to applied fields, but for many problems (those concerned with a narrow enough bandwidth) the frequency-dependence of
; can be neglected.
At a boundary,
, where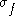 
is the free charge density.
system of units, D is measured in coulombs per square meter (C/m2).
This choice of units (together with measuring the magnetizing field H in ampere
s per meter (A/m)) is designed to absorb the electric and magnetic constants in the Maxwell's equations
expressed in terms of free charge and current, and results in very simple forms for
Gauss's law
and the Ampère-Maxwell equation:
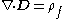
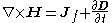
Choice of units has differed in history, for example in the Gaussian
CGS system of units the unit of charge is defined so that E and D are expressed in the same units.
placed in space (or in a medium) with no free charges present except on the capacitor. In SI
units, the charge density on the plates is equal to the value of the D field between the plates. This follows directly from Gauss's law
, by integrating over a small rectangular pillbox straddling one plate of the capacitor:
On the sides of the pillbox,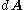
is perpendicular to the field, so that part of the integral is zero, leaving, for the space inside the capacitor where the fields of the two plates add
where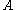
is surface area of the top face of the small rectangular pillbox and 
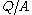is just the free surface charge density on the positive plate. Outside the capacitor, the fields of the two plates cancel each other and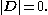 
If the space between the capacitor plates is filled with a linear homogeneous isotropic dielectric with permittivity
the electric field between the plates is constant: 
.
If the distance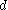
between the plates of a finite parallel plate capacitor is much smaller than its lateral dimensions
we can approximate it using the infinite case and obtain its capacitance
as
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the electric displacement field, denoted as
, is a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that appears in Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
It accounts for the effects of free
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
charges
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
within materials. "D" stands for "displacement," as in the related concept of displacement current
Displacement current
In electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
in dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
s. In free space, the electric displacement field is equivalent to flux density
Flux density
-Formal Statement:The flux density is simply defined as the amount of flux passing through a unit-area. -Mathematical Statement:The flux density would essentially be the number of field lines passing through a defined unit-area...
, a concept that lends understanding to Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
.
Definition
In a dielectricDielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
material the presence of an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E causes the bound charges in the material (atomic nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
and their electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s) to slightly separate, inducing a local
electric dipole moment
Electric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
. The electric displacement field D is defined as
where
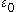is the vacuum permittivity (also called permittivity of free space),and P is the (macroscopic) density of the permanent and induced electric dipole moments in the material, called the polarization density
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
. Separating the total volume charge density into free and bound charges:
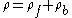
the density can be rewritten as a function of the polarization P:
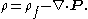
P is a vector field whose divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
yields the density of bound charges
in the material. The electric field satisfies the equation: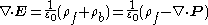and hence
.The displacement field therefore satisfies Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
in a dielectric:
.D is not determined exclusively by the free charge. Consider the relationship:
Which, by the fact that E has a curl of zero in electrostatic situations, evaluates to:
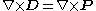
Which can be immediately seen in the case of some object with a "frozen in" polarization like a bar electret
Electret
Electret is a dielectric material that has a quasi-permanent electric charge or dipole polarisation. An electret generates internal and external electric fields, and is the electrostatic equivalent of a permanent magnet. Oliver Heaviside coined this term in 1885...
, the electric analogue to a bar magnet. There is no free charge in such a material, but the inherent polarization gives rise to an electric field. If the wayward student were to assume the D field were entirely determined by the free charge, he or she would immediately conclude the electric field were zero in such a material, but this is patently not true. The electric field can be properly determined by using the above relation along with other boundary conditions on the polarization density
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
yielding the bound charges, which will, in turn, yield the electric field.
In a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
, isotropic dielectric with instantaneous response to changes in the electric field, P depends linearly on the electric field,
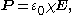
where the constant of proportionality
is called the electric susceptibilityElectric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
of the material. Thus
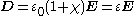
where
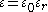is the permittivityPermittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
, and
the relative permittivityof the material.
In linear, homogeneous, isotropic media
is a constant. However, in linear anisotropic media it is a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, and in
nonhomogeneous media it is a function of position inside the medium. It may also depend upon the electric field (nonlinear materials) and have a time dependent response. Explicit time dependence can arise if the materials are physically moving or changing in time (e.g. reflections off a moving interface give rise to Doppler shifts). A different form of time dependence can arise in a time-invariant medium, in that there can be a time delay between the imposition of the electric field and the resulting polarization of the material. In this case, P is a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
susceptibility χ and the electric field E. Such a convolution takes on a simpler form in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
—by Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
ing the relationship and applying the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
, one obtains the following relation for a linear time-invariant medium:
where
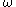is frequency of the applied field (e.g. in radian/s). The constraint of causalityCausality
Causality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
leads to the Kramers–Kronig relations, which place limitations upon the form of the frequency dependence. The phenomenon of a frequency-dependent permittivity is an example of material dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
. In fact, all physical materials have some material dispersion because they cannot respond instantaneously to applied fields, but for many problems (those concerned with a narrow enough bandwidth) the frequency-dependence of
; can be neglected.At a boundary,
, where 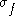is the free charge density.Units
In the standard SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
system of units, D is measured in coulombs per square meter (C/m2).
This choice of units (together with measuring the magnetizing field H in ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
s per meter (A/m)) is designed to absorb the electric and magnetic constants in the Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
expressed in terms of free charge and current, and results in very simple forms for
Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and the Ampère-Maxwell equation:
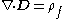
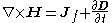
Choice of units has differed in history, for example in the Gaussian
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
CGS system of units the unit of charge is defined so that E and D are expressed in the same units.
Example: Displacement field in a capacitor
Consider an infinite parallel plate capacitorCapacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
placed in space (or in a medium) with no free charges present except on the capacitor. In SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units, the charge density on the plates is equal to the value of the D field between the plates. This follows directly from Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
, by integrating over a small rectangular pillbox straddling one plate of the capacitor:
On the sides of the pillbox,
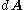is perpendicular to the field, so that part of the integral is zero, leaving, for the space inside the capacitor where the fields of the two plates add-
,
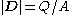where
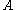is surface area of the top face of the small rectangular pillbox and 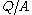is just the free surface charge density on the positive plate. Outside the capacitor, the fields of the two plates cancel each other and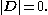 If the space between the capacitor plates is filled with a linear homogeneous isotropic dielectric with permittivity
the electric field between the plates is constant: .If the distance
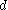between the plates of a finite parallel plate capacitor is much smaller than its lateral dimensionswe can approximate it using the infinite case and obtain its capacitance
Capacitance
In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
as
-
.
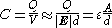See also
- Polarization densityPolarization densityIn classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
- Electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
- Magnetizing field
- Electric dipole momentElectric dipole momentIn physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...