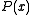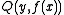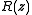Atomic formula
Encyclopedia
In mathematical logic
, an atomic formula (also known simply as an atom) is a formula with no deeper proposition
al structure, that is, a formula that contains no logical connective
s or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formula
s of the logic. Compound formulas are formed by combining the atomic formulas using the logical connectives.
The precise form of atomic formulas depends on the logic under consideration; for propositional logic, for example, the atomic formulas are the propositional variable
s. For predicate logic
, the atoms are predicate symbols together with their arguments, each argument being a term. In model theory
, atomic formula are merely strings
of symbols with a given signature
, which may or may not be satisfiable with respect to a given model.
have the following syntax
:
Terms
:
that is, a term is recursively defined
to be a constant c (a named object from the domain of discourse
), or a variable x (ranging over the objects in the domain of discourse), or an n-ary function f whose arguments are terms tk. Functions map tuple
s of objects to objects.
Propositions:
that is, a proposition is recursively defined to be an n-ary predicate P whose arguments are terms tk, or an expression composed of logical connective
s (and, or) and quantifiers (for-all, there-exists) used with other propositions.
An atomic formula or atom is simply a predicate applied to a tuple of terms; that is, an atomic formula is a formula of the form P (t1, …, tn) for P a predicate, and the tk terms.
All other well-formed formulae are obtained by composing atoms with logical connectives and quantifiers.
For example, the formula ∀x. P (x) ∧ ∃y. Q (y, f (x)) ∨ ∃z. R (z) contains the atoms
When all of the terms in an atom are ground terms, then the atom is called a ground atom or ground predicate.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, an atomic formula (also known simply as an atom) is a formula with no deeper proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
al structure, that is, a formula that contains no logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
s of the logic. Compound formulas are formed by combining the atomic formulas using the logical connectives.
The precise form of atomic formulas depends on the logic under consideration; for propositional logic, for example, the atomic formulas are the propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s. For predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
, the atoms are predicate symbols together with their arguments, each argument being a term. In model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, atomic formula are merely strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
of symbols with a given signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
, which may or may not be satisfiable with respect to a given model.
Atomic formula in first-order logic
The well-formed terms and propositions of ordinary first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
have the following syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
:
Terms
Term algebra
In universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set X of variables is exactly the free magma generated by X...
:
-
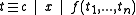 ,
,
that is, a term is recursively defined
Recursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
to be a constant c (a named object from the domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
), or a variable x (ranging over the objects in the domain of discourse), or an n-ary function f whose arguments are terms tk. Functions map tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of objects to objects.
Propositions:
-
 ,
,
that is, a proposition is recursively defined to be an n-ary predicate P whose arguments are terms tk, or an expression composed of logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s (and, or) and quantifiers (for-all, there-exists) used with other propositions.
An atomic formula or atom is simply a predicate applied to a tuple of terms; that is, an atomic formula is a formula of the form P (t1, …, tn) for P a predicate, and the tk terms.
All other well-formed formulae are obtained by composing atoms with logical connectives and quantifiers.
For example, the formula ∀x. P (x) ∧ ∃y. Q (y, f (x)) ∨ ∃z. R (z) contains the atoms
When all of the terms in an atom are ground terms, then the atom is called a ground atom or ground predicate.
See also
- In model theoryModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, structuresStructure (mathematical logic)In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
assign an interpretation to the atomic formulas. - In proof theoryProof theoryProof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, polarity assignment for atomic formulas is an essential component of focusing. - Atomic sentenceAtomic sentenceIn logic, an atomic sentence is a type of declarative sentence which is either true or false and which cannot be broken down into other simpler sentences...