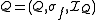Structure (mathematical logic)
Encyclopedia
In universal algebra
and in model theory
, a structure consists of a set along with a collection of finitary operations
and relations which are defined on it.
Universal algebra studies structures that generalize the algebraic structure
s such as groups
, rings
, fields
, vector space
s and lattices
. The term universal algebra is used for structures with no relation symbols.
Model theory has a different scope that encompasses more arbitrary theories, including foundational
structures such as models of set theory
. From the model-theoretic point of view, structures are the objects used to define the semantics of first-order logic
. In model theory a structure is often called just a model, although it is sometimes disambiguated as a semantic model when one discusses the notion in the more general setting of mathematical model
s. Logicians sometimes refer to structures as interpretation
s.
In database theory
, structures with no functions are studied as models for relational databases, in the form of relational model
s.
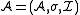 consisting of a domain A, a signature
consisting of a domain A, a signature
σ, and an interpretation function I that indicates how the signature is to be interpreted on the domain. To indicate that a structure has a particular signature σ one can refer to it as a σ-structure.
of a structure is an arbitrary set; it is also called the underlying set of the structure, its carrier (especially in universal algebra), or its universe (especially in model theory). Very often the definition of a structure prohibits the empty domain
.
Sometimes the notation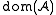 or
or 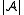 is used for the domain of
is used for the domain of 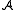 , but often no notational distinction is made between a structure and its domain. (I.e. the same symbol
, but often no notational distinction is made between a structure and its domain. (I.e. the same symbol 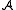 refers both to the structure and its domain.)
refers both to the structure and its domain.)
of a structure consists of a set of function symbols and relation symbols along with a function that ascribes to each symbol s a natural number
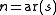 which is called the arity of s because it is the arity
which is called the arity of s because it is the arity
of the interpretation of s.
Since the signatures that arise in algebra
often contain only function symbols, a signature with no relation symbols is called an algebraic signature. A structure with such a signature is also called an algebra; this should not be confused with the notion of an algebra over a field
.
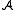 assigns functions and relations to the symbols of the signature. Each function symbol f of arity n is assigned an n-ary
assigns functions and relations to the symbols of the signature. Each function symbol f of arity n is assigned an n-ary
function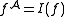 on the domain. Each relation symbol R of arity n is assigned an n-ary relation
on the domain. Each relation symbol R of arity n is assigned an n-ary relation 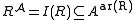 on the domain. A nullary function symbol c is called a constant symbol, because its interpretation I(c) can be identified with a constant element of the domain.
on the domain. A nullary function symbol c is called a constant symbol, because its interpretation I(c) can be identified with a constant element of the domain.
When a structure (and hence an interpretation function) is given by context, no notational distinction is made between a symbol s and its interpretation I(s). For example if f is a binary function symbol of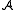 , one simply writes
, one simply writes 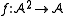 rather than
rather than 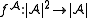 .
.
consists of two binary function symbols + and ×, a unary function symbol −, and the two constant symbols 0 and 1.
Thus a structure (algebra) for this signature consists of a set of elements A together with two binary functions, a unary function, and two distinguished elements; but there is no requirement that it satisfy any of the field axioms. The rational number
s Q, the real number
s R and the complex number
s C, like any other field, can be regarded as σ-structures in an obvious way:
where
and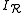 and
and 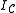 are similarly defined.
are similarly defined.
But the ring Z of integer
s, which is not a field, is also a σf-structure in the same way. In fact, there is no requirement that any of the field axioms hold in a σf-structure.
A signature for ordered field
s needs an additional binary relation such as < or ≤, and therefore structures for such a signature are not algebras, even though they are of course algebraic structure
s in the usual, loose sense of the word.
The ordinary signature for set theory includes a single binary relation ∈. A structure for this signature consists of a set of elements and an interpretation of the ∈ relation as a binary relation on these elements.
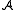 is called an (induced) substructure
is called an (induced) substructure
of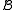 if
if
The usual notation for this relation is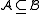 .
.
A subset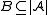 of the domain of a structure
of the domain of a structure 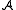 is called closed if it is closed under the functions of
is called closed if it is closed under the functions of 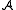 , i.e. if the following condition is satisfied: for every natural number n, every n-ary function symbol f (in the signature of
, i.e. if the following condition is satisfied: for every natural number n, every n-ary function symbol f (in the signature of 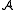 ) and all elements
) and all elements 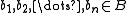 , the result of applying f to the n-tuple
, the result of applying f to the n-tuple 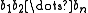 is again an element of B:
is again an element of B: 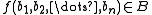 .
.
For every subset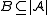 there is a smallest closed subset of
there is a smallest closed subset of 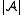 that contains B. It is called the closed subset generated by B, or the hull of B, and denoted by
that contains B. It is called the closed subset generated by B, or the hull of B, and denoted by 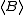 or
or 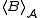 . The operator
. The operator 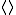 is a finitary closure operator on the set of subsets of
is a finitary closure operator on the set of subsets of 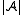 .
.
If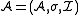 and
and 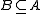 is a closed subset, then
is a closed subset, then 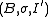 is an induced substructure of
is an induced substructure of 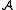 , where
, where 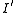 assigns to every symbol of σ the restriction to B of its interpretation in
assigns to every symbol of σ the restriction to B of its interpretation in 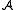 . Conversely, the domain of an induced substructure is a closed subset.
. Conversely, the domain of an induced substructure is a closed subset.
The closed subsets (or induced substructures) of a structure form a lattice
. The meet
of two subsets is their intersection. The join of two subsets is the closed subset generated by their union. Universal algebra studies the lattice of substructures of a structure in detail.
s form a substructure of the real number
s, and the real numbers form a substructure of the complex number
s. The rational numbers are the smallest substructure of the real (or complex) numbers that also satisfies the field axioms.
The set of integers gives an even smaller substructure of the real numbers which is not a field. Indeed, the integers are the substructure of the real numbers generated by the empty set, using this signature. The notion in abstract algebra that corresponds to a substructure of a field, in this signature, is that of a subring
, rather than that of a subfield.
The most obvious way to define a graph
is a structure with a signature σ consisting of a single binary relation symbol E. The vertices of the graph form the domain of the structure, and for two vertices a and b,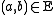 means that a and b are connected by an edge. In this encoding, the notion of induced substructure is more restrictive than the notion of subgraph. For example, let G be a graph consisting of two vertices connected by an edge, and let H be the graph consisting of the same vertices but no edges. H is a subgraph of G, but not an induced substructure. The notion in graph theory
means that a and b are connected by an edge. In this encoding, the notion of induced substructure is more restrictive than the notion of subgraph. For example, let G be a graph consisting of two vertices connected by an edge, and let H be the graph consisting of the same vertices but no edges. H is a subgraph of G, but not an induced substructure. The notion in graph theory
that corresponds to induced substructures is that of induced subgraphs.
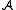 and
and 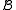 of the same signature σ, a (σ-)homomorphism from
of the same signature σ, a (σ-)homomorphism from 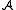 to
to 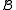 is a map
is a map
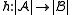 which preserves the functions and relations. More precisely:
which preserves the functions and relations. More precisely:
The notation for a homomorphism h from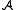 to
to 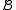 is
is 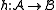 .
.
For every signature σ there is a concrete
category
σ-Hom which has σ-structures as objects and σ-homomorphisms as morphisms.
A homomorphism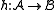 is sometimes called strong if for every n-ary relation symbol R and any elements
is sometimes called strong if for every n-ary relation symbol R and any elements 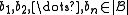 such that
such that 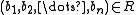 , there are
, there are 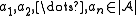 such that
such that 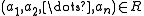 and
and 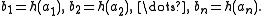
The strong homomorphisms give rise to a subcategory of σ-Hom.
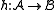 is called a (σ-)embedding if it is one-to-one
is called a (σ-)embedding if it is one-to-one
and
Thus an embedding is the same thing as a strong homomorphism which is one-to-one.
The category σ-Emb of σ-structures and σ-embeddings is a concrete subcategory
of σ-Hom.
Induced substructures correspond to subobject
s in σ-Emb. If σ has only function symbols, σ-Emb is the subcategory of monomorphism
s of σ-Hom. In this case induced substructures also correspond to subobjects in σ-Hom.
is the same thing as a homomorphism between the two structures coding the graph. In the example of the previous section, even though the subgraph H of G is not induced, the identity map id: H → G is a homomorphism. This map is in fact a monomorphism
in the category σ-Hom, and therefore H is a subobject
of G which is not an induced substructure.
Every constraint satisfaction problem
(CSP) has a translation into the homomorphism problem.
Therefore the complexity of CSP can be studied using the methods of finite model theory
.
Another application is in database theory
, where a relational model
of a database
is essentially the same thing as a relational structure. It turns out that a conjunctive query
on a database can be described by another structure in the same signature as the database model. A homomorphism from the relational model to the structure representing the query is the same thing as a solution to the query. This shows that the conjunctive query problem is also equivalent to the homomorphism problem.
. In connection with first-order logic and model theory, structures are often called models, even when the question "models of what?" has no obvious answer.
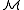 has a satisfaction relation
has a satisfaction relation 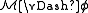 defined for all formulas
defined for all formulas 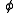 in the language consisting of the language of
in the language consisting of the language of 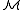 together with a constant symbol for each element of M, which is interpreted as that element.
together with a constant symbol for each element of M, which is interpreted as that element.
This relation is defined inductively using Tarski's T-schema
.
A structure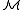 is said to be a model of a theory
is said to be a model of a theory
T if the language of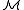 is the same as the language of T and every sentence in T is satisfied by
is the same as the language of T and every sentence in T is satisfied by 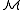 . Thus, for example, a "ring" is a structure for the language of rings that satisfies each of the ring axioms, and a model of ZFC set theory is a structure in the language of set theory that satisfies each of the ZFC axioms.
. Thus, for example, a "ring" is a structure for the language of rings that satisfies each of the ring axioms, and a model of ZFC set theory is a structure in the language of set theory that satisfies each of the ZFC axioms.
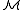 is said to be definable (or explicitly definable, or
is said to be definable (or explicitly definable, or 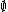 -definable) if there is a formula φ(x1,...,xn) such that
-definable) if there is a formula φ(x1,...,xn) such that
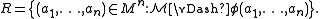
In other words, R is definable if and only if there is a formula φ such that
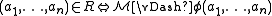
is correct.
An important special case is the definability of specific elements. An element m of M is definable in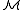 if and only if there is a formula φ(x) such that
if and only if there is a formula φ(x) such that
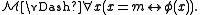
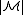 -definable) if there is a formula φ with parameters from
-definable) if there is a formula φ with parameters from 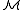 such that R is definable using φ. Every element of a structure is definable using the element itself as a parameter.
such that R is definable using φ. Every element of a structure is definable using the element itself as a parameter.
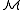 is explicitly definable if there is a formula φ(x1,...,xn) such that
is explicitly definable if there is a formula φ(x1,...,xn) such that
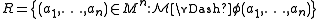
Here the formula φ used to define a relation R must be over the signature of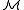 and so φ may not mention R itself, since R is not in the signature of
and so φ may not mention R itself, since R is not in the signature of 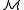 . If there is a formula φ in the extended language containing the language of
. If there is a formula φ in the extended language containing the language of 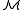 and a new symbol R, and the relation R is the only relation on
and a new symbol R, and the relation R is the only relation on 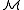 such that
such that 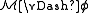 , then R is said to be implicitly definable over
, then R is said to be implicitly definable over 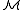 .
.
There are many examples of implicitly definable relations that are not explicitly definable.
Vector space
s, for example, can be regarded as two-sorted structures in the following way. The two-sorted signature of vector spaces consists of two sorts V (for vectors) and S (for scalars) and the following function symbols:
If V is a vector space over a field F, the corresponding two-sorted structure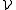 consists of the vector domain
consists of the vector domain 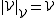 , the scalar domain
, the scalar domain 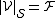 , and the obvious functions, such as the vector zero
, and the obvious functions, such as the vector zero 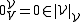 , the scalar zero
, the scalar zero 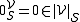 , or scalar multiplication
, or scalar multiplication 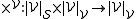 .
.
Many-sorted structures are often used as a convenient tool even when they could be avoided with a little effort. But they are rarely defined in a rigorous way, because it is straightforward and tedious (hence unrewarding) to carry out the generalization explicitly.
In most mathematical endeavours, not much attention is paid to the sorts. A many-sorted logic
however naturally leads to a type theory
. As Bart Jacobs puts it: "A logic is always a logic over a type theory." This emphasis in turn leads to categorical logic
because a logic over a type theory categorically corresponds to one ("total") category, capturing the logic, being fibred
over another ("base") category, capturing the type theory.
, but it is not a variety
. Universal algebra solves this problem by adding a unary function symbol −1.
In the case of fields this strategy works only for addition. For multiplication it fails because 0 does not have a multiplicative inverse. An ad hoc attempt to deal with this would be to define 0−1 = 0. (This attempt fails, essentially because with this definition 0 × 0−1 = 1 is not true.) Therefore one is naturally led to allow partial functions, i.e., functions which are defined only on a subset of their domain. However, there are several obvious ways to generalize notions such as substructure, homomorphism and identity.
, there are many sorts of variables, each of which has a type. Types are inductively defined; given two types δ and σ there is also a type σ → δ that represents functions from objects of type σ to objects of type δ. A structure for a typed language (in the ordinary first-order semantics) must include a separate set of objects of each type, and for a function type the structure must have complete information about the function represented by each object of that type.
, as discussed in the article on second-order logic
. When using full higher-order semantics, a structure need only have a universe for objects of type 0, and the T-schema is extended so that a quantifier over a higher-order type is satisfied by the model if and only if it is disquotationally true. When using first-order semantics, an additional sort is added for each higher-order type, as in the case of a many sorted first order language.
and category theory
, it is sometimes useful to consider structures in which the domain of discourse is a proper class instead of a set. These structures are sometimes called class models to distinguish them from the "set models" discussed above. When the domain is a proper class, each function and relation symbol may also be represented by a proper class.
In Bertrand Russell
's Principia Mathematica
, structures were also allowed to have a proper class as their domain.
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
and in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a structure consists of a set along with a collection of finitary operations
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
and relations which are defined on it.
Universal algebra studies structures that generalize the algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s such as groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. The term universal algebra is used for structures with no relation symbols.
Model theory has a different scope that encompasses more arbitrary theories, including foundational
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
structures such as models of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. From the model-theoretic point of view, structures are the objects used to define the semantics of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. In model theory a structure is often called just a model, although it is sometimes disambiguated as a semantic model when one discusses the notion in the more general setting of mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s. Logicians sometimes refer to structures as interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
s.
In database theory
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
, structures with no functions are studied as models for relational databases, in the form of relational model
Relational model
The relational model for database management is a database model based on first-order predicate logic, first formulated and proposed in 1969 by Edgar F...
s.
Definition
Formally, a structure can be defined as a triple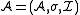 consisting of a domain A, a signature
consisting of a domain A, a signatureSignature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ, and an interpretation function I that indicates how the signature is to be interpreted on the domain. To indicate that a structure has a particular signature σ one can refer to it as a σ-structure.
Domain
The domainDomain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
of a structure is an arbitrary set; it is also called the underlying set of the structure, its carrier (especially in universal algebra), or its universe (especially in model theory). Very often the definition of a structure prohibits the empty domain
Empty domain
In first-order logic the empty domain is the empty set having no members. In traditional and classical logic domains are restrictedly non-empty in order that certain theorems be valid. Interpretations with an empty domain are shown to be a trivial case by a convention originating at least in 1927...
.
Sometimes the notation
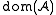 or
or 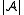 is used for the domain of
is used for the domain of 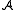 , but often no notational distinction is made between a structure and its domain. (I.e. the same symbol
, but often no notational distinction is made between a structure and its domain. (I.e. the same symbol 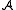 refers both to the structure and its domain.)
refers both to the structure and its domain.)Signature
The signatureSignature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
of a structure consists of a set of function symbols and relation symbols along with a function that ascribes to each symbol s a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
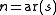 which is called the arity of s because it is the arity
which is called the arity of s because it is the arityArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
of the interpretation of s.
Since the signatures that arise in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
often contain only function symbols, a signature with no relation symbols is called an algebraic signature. A structure with such a signature is also called an algebra; this should not be confused with the notion of an algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
.
Interpretation function
The interpretation function I of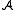 assigns functions and relations to the symbols of the signature. Each function symbol f of arity n is assigned an n-ary
assigns functions and relations to the symbols of the signature. Each function symbol f of arity n is assigned an n-aryArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
function
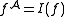 on the domain. Each relation symbol R of arity n is assigned an n-ary relation
on the domain. Each relation symbol R of arity n is assigned an n-ary relation 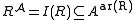 on the domain. A nullary function symbol c is called a constant symbol, because its interpretation I(c) can be identified with a constant element of the domain.
on the domain. A nullary function symbol c is called a constant symbol, because its interpretation I(c) can be identified with a constant element of the domain.When a structure (and hence an interpretation function) is given by context, no notational distinction is made between a symbol s and its interpretation I(s). For example if f is a binary function symbol of
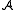 , one simply writes
, one simply writes 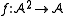 rather than
rather than 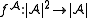 .
.Examples
The standard signature σf for fieldsField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
consists of two binary function symbols + and ×, a unary function symbol −, and the two constant symbols 0 and 1.
Thus a structure (algebra) for this signature consists of a set of elements A together with two binary functions, a unary function, and two distinguished elements; but there is no requirement that it satisfy any of the field axioms. The rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q, the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R and the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C, like any other field, can be regarded as σ-structures in an obvious way:
where
-
 is addition of rational numbers,
is addition of rational numbers, is multiplication of rational numbers,
is multiplication of rational numbers,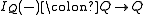 is the function that takes each rational number x to -x, and
is the function that takes each rational number x to -x, and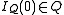 is the number 0 and
is the number 0 and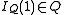 is the number 1;
is the number 1;
and
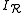 and
and 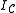 are similarly defined.
are similarly defined.But the ring Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, which is not a field, is also a σf-structure in the same way. In fact, there is no requirement that any of the field axioms hold in a σf-structure.
A signature for ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s needs an additional binary relation such as < or ≤, and therefore structures for such a signature are not algebras, even though they are of course algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s in the usual, loose sense of the word.
The ordinary signature for set theory includes a single binary relation ∈. A structure for this signature consists of a set of elements and an interpretation of the ∈ relation as a binary relation on these elements.
Induced substructures and closed subsets
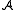 is called an (induced) substructure
is called an (induced) substructureSubstructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
of
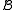 if
if
-
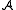 and
and  have the same signature
have the same signature 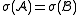 ;
; - the domain of
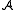 is contained in the domain of
is contained in the domain of  :
:  ; and
; and - the interpretations of all function and relation symbols agree on
 .
.
The usual notation for this relation is
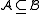 .
.A subset
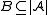 of the domain of a structure
of the domain of a structure 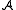 is called closed if it is closed under the functions of
is called closed if it is closed under the functions of 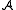 , i.e. if the following condition is satisfied: for every natural number n, every n-ary function symbol f (in the signature of
, i.e. if the following condition is satisfied: for every natural number n, every n-ary function symbol f (in the signature of 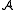 ) and all elements
) and all elements 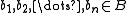 , the result of applying f to the n-tuple
, the result of applying f to the n-tuple 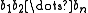 is again an element of B:
is again an element of B: 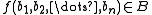 .
.For every subset
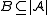 there is a smallest closed subset of
there is a smallest closed subset of 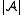 that contains B. It is called the closed subset generated by B, or the hull of B, and denoted by
that contains B. It is called the closed subset generated by B, or the hull of B, and denoted by 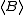 or
or 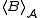 . The operator
. The operator 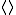 is a finitary closure operator on the set of subsets of
is a finitary closure operator on the set of subsets of 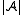 .
.If
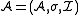 and
and 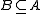 is a closed subset, then
is a closed subset, then 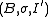 is an induced substructure of
is an induced substructure of 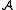 , where
, where 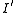 assigns to every symbol of σ the restriction to B of its interpretation in
assigns to every symbol of σ the restriction to B of its interpretation in 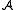 . Conversely, the domain of an induced substructure is a closed subset.
. Conversely, the domain of an induced substructure is a closed subset.The closed subsets (or induced substructures) of a structure form a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. The meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
of two subsets is their intersection. The join of two subsets is the closed subset generated by their union. Universal algebra studies the lattice of substructures of a structure in detail.
Examples
Let σ = {+, ×, −, 0, 1} be again the standard signature for fields. When regarded as σ-structures in the natural way, the rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s form a substructure of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and the real numbers form a substructure of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. The rational numbers are the smallest substructure of the real (or complex) numbers that also satisfies the field axioms.
The set of integers gives an even smaller substructure of the real numbers which is not a field. Indeed, the integers are the substructure of the real numbers generated by the empty set, using this signature. The notion in abstract algebra that corresponds to a substructure of a field, in this signature, is that of a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
, rather than that of a subfield.
The most obvious way to define a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is a structure with a signature σ consisting of a single binary relation symbol E. The vertices of the graph form the domain of the structure, and for two vertices a and b,
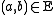 means that a and b are connected by an edge. In this encoding, the notion of induced substructure is more restrictive than the notion of subgraph. For example, let G be a graph consisting of two vertices connected by an edge, and let H be the graph consisting of the same vertices but no edges. H is a subgraph of G, but not an induced substructure. The notion in graph theory
means that a and b are connected by an edge. In this encoding, the notion of induced substructure is more restrictive than the notion of subgraph. For example, let G be a graph consisting of two vertices connected by an edge, and let H be the graph consisting of the same vertices but no edges. H is a subgraph of G, but not an induced substructure. The notion in graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
that corresponds to induced substructures is that of induced subgraphs.
Homomorphisms
Given two structures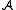 and
and 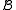 of the same signature σ, a (σ-)homomorphism from
of the same signature σ, a (σ-)homomorphism from 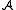 to
to 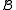 is a map
is a mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
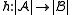 which preserves the functions and relations. More precisely:
which preserves the functions and relations. More precisely:- For every n-ary function symbol f of σ and any elements
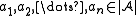 , the following equation holds:
, the following equation holds:
-
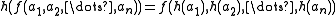 .
.
- For every n-ary relation symbol R of σ and any elements
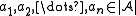 , the following implication holds:
, the following implication holds:
- For every n-ary relation symbol R of σ and any elements
 .
.
The notation for a homomorphism h from
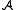 to
to 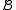 is
is 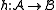 .
.For every signature σ there is a concrete
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
σ-Hom which has σ-structures as objects and σ-homomorphisms as morphisms.
A homomorphism
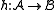 is sometimes called strong if for every n-ary relation symbol R and any elements
is sometimes called strong if for every n-ary relation symbol R and any elements 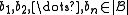 such that
such that 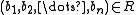 , there are
, there are 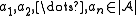 such that
such that 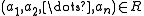 and
and 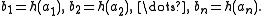
The strong homomorphisms give rise to a subcategory of σ-Hom.
Embeddings
A (σ-)homomorphism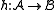 is called a (σ-)embedding if it is one-to-one
is called a (σ-)embedding if it is one-to-oneInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and
- for every n-ary relation symbol R of σ and any elements
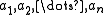 , the following equivalence holds:
, the following equivalence holds:
-
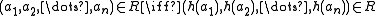 .
.
Thus an embedding is the same thing as a strong homomorphism which is one-to-one.
The category σ-Emb of σ-structures and σ-embeddings is a concrete subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of σ-Hom.
Induced substructures correspond to subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s in σ-Emb. If σ has only function symbols, σ-Emb is the subcategory of monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s of σ-Hom. In this case induced substructures also correspond to subobjects in σ-Hom.
Example
As seen above, in the standard encoding of graphs as structures the induced substructures are precisely the induced subgraphs. However, a homomorphism between graphsGraph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
is the same thing as a homomorphism between the two structures coding the graph. In the example of the previous section, even though the subgraph H of G is not induced, the identity map id: H → G is a homomorphism. This map is in fact a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
in the category σ-Hom, and therefore H is a subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
of G which is not an induced substructure.
Homomorphism problem
The following problem is known as the homomorphism problem:- Given two finite structures
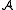 and
and 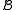 of a finite relational signature, find a homomorphism
of a finite relational signature, find a homomorphism 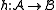 or show that no such homomorphism exists.
or show that no such homomorphism exists.
Every constraint satisfaction problem
Constraint satisfaction problem
Constraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
(CSP) has a translation into the homomorphism problem.
Therefore the complexity of CSP can be studied using the methods of finite model theory
Finite model theory
Finite Model Theory is a subarea of model theory . MT is the branch of mathematical logic which deals with the relation between a formal language and its interpretations . FMT is a restriction of MT to interpretations of finite structures, i.e...
.
Another application is in database theory
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
, where a relational model
Relational model
The relational model for database management is a database model based on first-order predicate logic, first formulated and proposed in 1969 by Edgar F...
of a database
Database
A database is an organized collection of data for one or more purposes, usually in digital form. The data are typically organized to model relevant aspects of reality , in a way that supports processes requiring this information...
is essentially the same thing as a relational structure. It turns out that a conjunctive query
Conjunctive query
In database theory, a conjunctive query is a restricted form of first-order queries. A large part of queries issued on relational databases can be written as conjunctive queries, and large parts of other first-order queries can be written as conjunctive queries....
on a database can be described by another structure in the same signature as the database model. A homomorphism from the relational model to the structure representing the query is the same thing as a solution to the query. This shows that the conjunctive query problem is also equivalent to the homomorphism problem.
Structures and first-order logic
Structures are sometimes referred to as "first-order structures". This is misleading, as nothing in their definition ties them to any specific logic, and in fact they are suitable as semantic objects both for very restricted fragments of first-order logic such as that used in universal algebra, and for second-order logicSecond-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. In connection with first-order logic and model theory, structures are often called models, even when the question "models of what?" has no obvious answer.
Satisfaction relation
Each first-order structure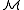 has a satisfaction relation
has a satisfaction relation 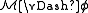 defined for all formulas
defined for all formulas 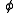 in the language consisting of the language of
in the language consisting of the language of 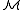 together with a constant symbol for each element of M, which is interpreted as that element.
together with a constant symbol for each element of M, which is interpreted as that element.This relation is defined inductively using Tarski's T-schema
T-schema
The T-schema or truth schema is used to give an inductive definition of truth which lies at the heart of any realisation of Alfred Tarski's semantic theory of truth...
.
A structure
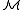 is said to be a model of a theory
is said to be a model of a theoryTheory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
T if the language of
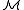 is the same as the language of T and every sentence in T is satisfied by
is the same as the language of T and every sentence in T is satisfied by 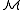 . Thus, for example, a "ring" is a structure for the language of rings that satisfies each of the ring axioms, and a model of ZFC set theory is a structure in the language of set theory that satisfies each of the ZFC axioms.
. Thus, for example, a "ring" is a structure for the language of rings that satisfies each of the ring axioms, and a model of ZFC set theory is a structure in the language of set theory that satisfies each of the ZFC axioms.Definable relations
An n-ary relation R on the universe M of a structure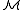 is said to be definable (or explicitly definable, or
is said to be definable (or explicitly definable, or 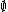 -definable) if there is a formula φ(x1,...,xn) such that
-definable) if there is a formula φ(x1,...,xn) such that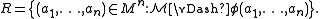
In other words, R is definable if and only if there is a formula φ such that
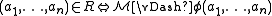
is correct.
An important special case is the definability of specific elements. An element m of M is definable in
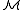 if and only if there is a formula φ(x) such that
if and only if there is a formula φ(x) such that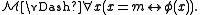
Definability with parameters
A relation R is said to be definable with parameters (or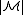 -definable) if there is a formula φ with parameters from
-definable) if there is a formula φ with parameters from 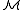 such that R is definable using φ. Every element of a structure is definable using the element itself as a parameter.
such that R is definable using φ. Every element of a structure is definable using the element itself as a parameter.Implicit definability
Recall from above that an n-ary relation R on the universe M of a structure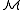 is explicitly definable if there is a formula φ(x1,...,xn) such that
is explicitly definable if there is a formula φ(x1,...,xn) such that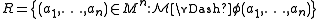
Here the formula φ used to define a relation R must be over the signature of
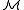 and so φ may not mention R itself, since R is not in the signature of
and so φ may not mention R itself, since R is not in the signature of 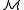 . If there is a formula φ in the extended language containing the language of
. If there is a formula φ in the extended language containing the language of 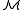 and a new symbol R, and the relation R is the only relation on
and a new symbol R, and the relation R is the only relation on 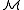 such that
such that 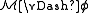 , then R is said to be implicitly definable over
, then R is said to be implicitly definable over 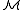 .
.There are many examples of implicitly definable relations that are not explicitly definable.
Many-sorted structures
Structures as defined above are sometimes called s to distinguish them from the more general s. A many-sorted structure can have an arbitrary number of domains. The sorts are part of the signature, and they play the role of names for the different domains. Many-sorted signatures also prescribe on which sorts the functions and relations of a many-sorted structure are defined. Therefore the arities of function symbols or relation symbols must be more complicated objects such as tuples of sorts rather than natural numbers.Vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, for example, can be regarded as two-sorted structures in the following way. The two-sorted signature of vector spaces consists of two sorts V (for vectors) and S (for scalars) and the following function symbols:
|
|
|
If V is a vector space over a field F, the corresponding two-sorted structure
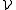 consists of the vector domain
consists of the vector domain 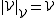 , the scalar domain
, the scalar domain 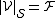 , and the obvious functions, such as the vector zero
, and the obvious functions, such as the vector zero 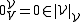 , the scalar zero
, the scalar zero 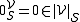 , or scalar multiplication
, or scalar multiplication 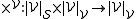 .
.Many-sorted structures are often used as a convenient tool even when they could be avoided with a little effort. But they are rarely defined in a rigorous way, because it is straightforward and tedious (hence unrewarding) to carry out the generalization explicitly.
In most mathematical endeavours, not much attention is paid to the sorts. A many-sorted logic
Many-sorted logic
Many-sorted logic can reflect formally our intention, not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming...
however naturally leads to a type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
. As Bart Jacobs puts it: "A logic is always a logic over a type theory." This emphasis in turn leads to categorical logic
Categorical logic
Categorical logic is a branch of category theory within mathematics, adjacent to mathematical logic but more notable for its connections to theoretical computer science. In broad terms, categorical logic represents both syntax and semantics by a category, and an interpretation by a functor...
because a logic over a type theory categorically corresponds to one ("total") category, capturing the logic, being fibred
Fibred category
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined...
over another ("base") category, capturing the type theory.
Partial algebras
Both universal algebra and model theory study classes of (structures or) algebras that are defined by a signature and a set of axioms. In the case of model theory these axioms have the form of first-order sentences. The formalism of universal algebra is much more restrictive; essentially it only allows first-order sentences that have the form of universally quantified equations between terms, e.g. x y (x + y = y + x). One consequence is that the choice of a signature is more significant in universal algebra than it is in model theory. For example the class of groups, in the signature consisting of the binary function symbol × and the constant symbol 1, is an elementary classElementary class
In the branch of mathematical logic called model theory, an elementary class is a class consisting of all structures satisfying a fixed first-order theory.- Definition :...
, but it is not a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
. Universal algebra solves this problem by adding a unary function symbol −1.
In the case of fields this strategy works only for addition. For multiplication it fails because 0 does not have a multiplicative inverse. An ad hoc attempt to deal with this would be to define 0−1 = 0. (This attempt fails, essentially because with this definition 0 × 0−1 = 1 is not true.) Therefore one is naturally led to allow partial functions, i.e., functions which are defined only on a subset of their domain. However, there are several obvious ways to generalize notions such as substructure, homomorphism and identity.
Structures for typed languages
In type theoryType theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, there are many sorts of variables, each of which has a type. Types are inductively defined; given two types δ and σ there is also a type σ → δ that represents functions from objects of type σ to objects of type δ. A structure for a typed language (in the ordinary first-order semantics) must include a separate set of objects of each type, and for a function type the structure must have complete information about the function represented by each object of that type.
Higher-order languages
There is more than one possible semantics for higher-order logicHigher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
, as discussed in the article on second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. When using full higher-order semantics, a structure need only have a universe for objects of type 0, and the T-schema is extended so that a quantifier over a higher-order type is satisfied by the model if and only if it is disquotationally true. When using first-order semantics, an additional sort is added for each higher-order type, as in the case of a many sorted first order language.
Structures that are proper classes
In the study of set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, it is sometimes useful to consider structures in which the domain of discourse is a proper class instead of a set. These structures are sometimes called class models to distinguish them from the "set models" discussed above. When the domain is a proper class, each function and relation symbol may also be represented by a proper class.
In Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
's Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
, structures were also allowed to have a proper class as their domain.
External links
- Semantics section in Classical Logic (an entry of Stanford Encyclopedia of Philosophy)