
Substructure
Encyclopedia
In mathematical logic
, an (induced) substructure or (induced) subalgebra is a structure
whose domain is a subset
of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure. Some examples of subalgebras are subgroup
s, submonoids, subring
s, subfields, subalgebras of algebras over a field
, or induced subgraphs. Shifting the point of view, the larger structure is called an extension or a superstructure of its substructure.
In model theory
, the term "submodel" is often used as a synonym for substructure, especially when the context suggests a theory of which both structures are models.
In the presence of relations (i.e. for structures such as ordered group
s or graph
s, whose signature
is not functional) it may make sense to relax the conditions on a subalgebra so that the relations on a weak substructure (or weak subalgebra) are at most those induced from the bigger structure. Subgraphs are an example where the distinction matters, and the term "subgraph" does indeed refer to weak substructures. Ordered group
s, on the other hand, have the special property that every substructure of an ordered group which is itself an ordered group, is an induced substructure.
A and B of the same signature
σ, A is said to be a weak substructure of B, or a weak subalgebra of B, if
A is said to be an (induced) substructure of B, or an (induced) subalgebra of B, if A is a weak subalgebra of B and, moreover,
If A is a substructure of B, then B is called a superstructure of A or, especially if A is an induced substructure, an extension of A.
(or just a field
) are precisely its subfields. Similarly, in the language (×, -1, 1) of groups, the substructures of a group
are its subgroup
s. In the language (×, 1) of monoids, however, the substructures of a group are its submonoids. They need need not be groups; and even if they are groups, they need not be subgroups.
In the case of graph
s (in the signature consisting of one binary relation), the induced substructures of a graph are precisely its induced subgraphs, and its weak substructures are precisely its subgraphs.
s in the concrete category
of σ-structures and strong homomorphisms (and also in the concrete category
of σ-structures and σ-embeddings). Weak substructures of σ-structures are the subobject
s in the concrete category
of σ-structures and homomorphisms in the ordinary sense.
Other examples:
In the category
of models of a theory and embedding
s between them, the submodels of a model are its subobject
s.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, an (induced) substructure or (induced) subalgebra is a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
whose domain is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure. Some examples of subalgebras are subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, submonoids, subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s, subfields, subalgebras of algebras over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, or induced subgraphs. Shifting the point of view, the larger structure is called an extension or a superstructure of its substructure.
In model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the term "submodel" is often used as a synonym for substructure, especially when the context suggests a theory of which both structures are models.
In the presence of relations (i.e. for structures such as ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
s or graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s, whose signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
is not functional) it may make sense to relax the conditions on a subalgebra so that the relations on a weak substructure (or weak subalgebra) are at most those induced from the bigger structure. Subgraphs are an example where the distinction matters, and the term "subgraph" does indeed refer to weak substructures. Ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
s, on the other hand, have the special property that every substructure of an ordered group which is itself an ordered group, is an induced substructure.
Definition
Given two structuresStructure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
A and B of the same signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ, A is said to be a weak substructure of B, or a weak subalgebra of B, if
- the domain of A is a subset of the domain of B,
- f A = f B | An for every n-ary function symbol f in σ, and
- R A
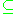 R B
R B  An for every n-ary relation symbol R in σ.
An for every n-ary relation symbol R in σ.
A is said to be an (induced) substructure of B, or an (induced) subalgebra of B, if A is a weak subalgebra of B and, moreover,
- R A = R B
 An for every n-ary relation symbol R in σ.
An for every n-ary relation symbol R in σ.
If A is a substructure of B, then B is called a superstructure of A or, especially if A is an induced substructure, an extension of A.
Example
In the language consisting of the binary functions + and ×, binary relation <, and constants 0 and 1, the structure (Q, +, ×, <, 0, 1) is a substructure of (R, +, ×, <, 0, 1). More generally, the substructures of an ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
(or just a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) are precisely its subfields. Similarly, in the language (×, -1, 1) of groups, the substructures of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
are its subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s. In the language (×, 1) of monoids, however, the substructures of a group are its submonoids. They need need not be groups; and even if they are groups, they need not be subgroups.
In the case of graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s (in the signature consisting of one binary relation), the induced substructures of a graph are precisely its induced subgraphs, and its weak substructures are precisely its subgraphs.
Substructures as subobjects
For every signature σ, induced substructures of σ-structures are the subobjectSubobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s in the concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
of σ-structures and strong homomorphisms (and also in the concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
of σ-structures and σ-embeddings). Weak substructures of σ-structures are the subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s in the concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
of σ-structures and homomorphisms in the ordinary sense.
Submodel
In model theory, given a structure M which is a model of a theory T, a submodel of M in a narrower sense is a substructure of M which is also a model of T. For example if T is the theory of abelian groups in the signature (+, 0), then the submodels of the group of integers (Z, +, 0) are the substructures which are also groups. Thus the natural numbers (N, +, 0) form a substructure of (Z, +, 0) which is not a submodel, while the even numbers (2Z, +, 0) form a submodel which is (a group but) not a subgroup.Other examples:
- The algebraic numbers form a submodel of the complex numbers in the theory of algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
s. - The rational numbers form a submodel of the real numbers in the theory of fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s. - Every elementary substructureElementary substructureIn model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
of a model of a theory T also satisfies T; hence it is a submodel.
In the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of models of a theory and embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s between them, the submodels of a model are its subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s.
See also
- Elementary substructureElementary substructureIn model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
- End extension
- Löwenheim-Skolem theorem
- Prime modelPrime modelIn mathematics, and in particular model theory, a prime model is a model which is as simple as possible. Specifically, a model P is prime if it admits an elementary embedding into any model M to which it is elementarily equivalent .- Cardinality :In contrast with the notion of saturated model,...

