Right quotient
Encyclopedia
The right quotient of a formal language
with a formal language 
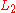is the language consisting of strings w such that wx is in 
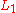for some string x in 
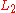. In symbols, we write:
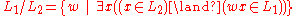
In other words, each string in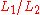
is the prefix of a string 
in 
, with the remainder of the word being a string in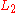 
.
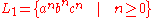
and
.
Now, if we insert a divider into the middle of an element of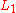
, the part on the right is in 
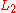only if the divider is placed adjacent to a b (in which case i ≤ n and j = n) or adjacent to a c (in which case i = 0 and j ≤ n). The part on the left, therefore, will be either 
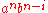or 
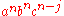; and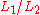 
can be written as
.
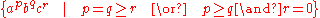, which keeps the postfixes of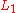
without the prefixes in 
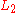. Sometimes, though, "right quotient" is written simply as "quotient". The above closure properties hold for both left and right quotients.
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
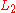with a formal language is the language consisting of strings w such that wx is in 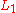for some string x in 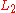. In symbols, we write: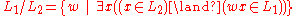In other words, each string in
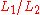is the prefix of a string in , with the remainder of the word being a string in 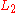.Examples
Consider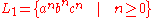and
.Now, if we insert a divider into the middle of an element of
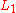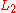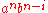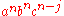, the part on the right is in only if the divider is placed adjacent to a b (in which case i ≤ n and j = n) or adjacent to a c (in which case i = 0 and j ≤ n). The part on the left, therefore, will be either or ; and 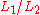can be written as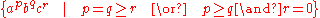.Properties
Some common closure properties of the right quotient include:- The quotient of a regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
with any other language is regular. - The quotient of a context free language with a regular language is context free.
- The quotient of two context free languages can be any recursively enumerable language.
- The quotient of two recursively enumerable languages is recursively enumerable.
Left and right quotients
There is a related notion of left quotientLeft quotient
If L_1 and L_2 are formal languages, then the left quotient of L_1 with L_2 is the language consisting of strings w such that xw is in L_2 for some string x in L_1...
, which keeps the postfixes of
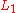without the prefixes in 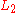. Sometimes, though, "right quotient" is written simply as "quotient". The above closure properties hold for both left and right quotients.