LR parser
Encyclopedia
In computer science
, an LR parser is a parser that reads input from Left to right (as it would appear if visually displayed) and produces a Rightmost derivation. The term LR(k) parser is also used; where the k refers to the number of unconsumed "look ahead
" input symbols that are used in making parsing decisions. Usually k is 1 and the term LR parser is often intended to refer to this case.
LR parsing can handle a larger range of languages than LL parsing, and is also better at error reporting, i.e. it detects syntactic errors when the input does not conform to the grammar as soon as possible. This is in contrast to an LL(k) (or even worse, an LL(*) parser) which may defer error detection to a different branch of the grammar due to backtracking, often making errors harder to localize across disjunctions with long common prefixes.
LR parsers are difficult to produce by hand and they are usually constructed by a parser generator or a compiler-compiler
. Depending on how the parsing table is generated, these parsers can be called simple LR parser
s (SLR), look-ahead LR parsers
(LALR), or canonical LR parser
s. LALR parsers have more language recognition power than SLR parsers. Canonical LR parsers have more recognition power than LALR parsers.
In this paper, Donald Knuth proves that
"LR(k) grammars can be efficiently parsed with an execution time essentially proportional to the length of string",
and that "A language can be generated by an LR(k) grammar if and only if it is deterministic, if and only if it can be generated by an LR(1) grammar" .
A deterministic context-free language
is a language for which some LR(k) grammar exists. Every LR(k) grammar for k > 1 can be mechanically transformed into an LR(1) grammar for the same language, while an LR(0) grammar for the same language may not exist; the LR(0) languages are a proper subset of the deterministic ones.
LR parsing can be generalized as arbitrary context-free language parsing without a performance penalty, even for LR(k) grammars. Note that the parsing of non-LR(k) context-free grammars is an order of magnitude slower (cubic instead of quadratic in relation to the input length).
The syntax of many programming language
s are defined by a grammar that is LR(k) (where k is a small constant, usually 1), or close to being so, and for this reason LR parsers are often used by compiler
s to perform syntax analysis of source code
.
An LR parser can be created from a context-free grammar
by a program called a parser generator or hand written by a programmer. A context-free grammar is classified as LR(k) if there exists an LR(k) parser for it, as determined by the parser generator.
An LR parser is said to perform bottom-up parsing
because it attempts to deduce the top level grammar productions by building up from the leaves.
An LR parser is based on an algorithm which is driven by a parser table, a data structure which contains the syntax of the computer language being parsed. So the term LR parser actually refers to a class of parser that can process almost any programming language, as long as the parser table for a programming language is supplied. The parser table is created by a program called a parser generator.
 Conceptually, an LR Parser is a recursive program that can be proven correct by direct computation, and can be implemented more efficiently (in time) as a recursive ascent parser
Conceptually, an LR Parser is a recursive program that can be proven correct by direct computation, and can be implemented more efficiently (in time) as a recursive ascent parser
, a set of mutually-recursive functions for every grammar, much like a recursive descent parser
. Conventionally, however, LR parsers are presented and implemented as table-based stack machines in which the call stack
of the underlying recursive program is explicitly manipulated.
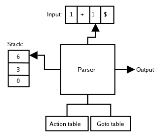
A table
-driven bottom-up parser can be schematically presented as in Figure 1. The following describes a rightmost derivation by this parser.
Since the LR parser reads input from left to right but needs to produce a rightmost derivation, it uses reductions, instead of derivations to process input. That is, the algorithm works by creating a "leftmost reduction" of the input. The end result, when reversed, will be a rightmost derivation.
The LR parsing algorithm works as follows:
and parse the following input:
The action table is indexed by a state of the parser and a terminal (including a special terminal $ that indicates the end of the input stream) and contains three types of actions:
The goto table is indexed by a state of the parser and a nonterminal and simply indicates what the next state of the parser will be if it has recognized a certain nonterminal. This table is important to find out the next state after every reduction. After a reduction, the next state is found by looking up the goto table entry for top of the stack (i.e. current state) and the reduced rule's LHS (i.e. non-terminal).
The first symbol from the input string that the parser sees is '1'. In order to find out what the next action is (shift, reduce, accept or error), the action table is indexed with the current state (remember that the "current state" is just whatever is on the top of the stack), which in this case is 0, and the current input symbol, which is '1'. The action table specifies a shift to state 2, and so state 2 is pushed onto the stack (again, remember that all the state information is in the stack, so "shifting to state 2" is the same thing as pushing 2 onto the stack). The resulting stack is
where the top of the stack is 2. For the sake of explanation we also show the symbol (e.g., '1', B) that caused the transition to the next state, although strictly speaking it is not part of the stack.
In state 2 the action table says that regardless of what terminal we see on the input stream, we should do a reduction with grammar rule 5. If the table is correct, this means that the parser has just recognized the right-hand side of rule 5, which is indeed the case.
In this case we write 5 to the output stream, pop one state from the stack (since the right-hand side of the rule has one symbol), and push on the stack the state from the cell in the goto table for state 0 and B, i.e., state 4. The resulting stack is:
However, in state 4 the action table says we should now do a reduction with rule 3. So we write 3 to the output stream, pop one state from the stack, and find the new state in the goto table for state 0 and E, which is state 3. The resulting stack:
The next terminal that the parser sees is a '+' and according to the action table it should then go to state 6:
Note that the resulting stack can be interpreted as the history of a finite state automaton that has just read a nonterminal E followed by a terminal '+'. The transition table of this automaton is defined by the shift actions in the action table and the goto actions in the goto table.
The next terminal is now '1' and this means that we perform a shift and go to state 2:
Just as the previous '1' this one is reduced to B giving the following stack:
Again note that the stack corresponds with a list of states of a finite automaton that has read a nonterminal E, followed by a '+' and then a nonterminal B. In state 8 we always perform a reduce with rule 2. Note that the top 3 states on the stack correspond with the 3 symbols in the right-hand side of rule 2.
Finally, we read a '$' from the input stream which means that according to the action table (the current state is 3) the parser accepts the input string.
The rule numbers that will then have been written to the output stream will be [5, 3, 5, 2] which is indeed a rightmost derivation of the string "1 + 1" in reverse.
Rules of the form A → ε have only a single item A → •. The item E → E • + B, for example, indicates that the parser has recognized a string corresponding with E on the input stream and now expects to read a '+' followed by another string corresponding with B.
where S is a new start symbol and E the old start symbol. The parser will use this rule for reduction exactly when it has accepted the input string.
For our example we will take the same grammar as before and augment it:
It is for this augmented grammar that we will determine the item sets and the transitions between them.
The boldfaced "+" in front of an item indicates the items that were added for the closure (not to be confused with the mathematical '+' operator which is a terminal). The original items without a "+" are called the kernel of the item set.
Starting at the begin state (S0) we will now determine all the states that can be reached from this state. The possible transitions for an item set can be found by looking at the symbols (terminals and nonterminals) we find right after the dots; in the case of item set 0 those symbols are the terminals '0' and '1' and the nonterminals E and B. To find the item set that each symbol x leads to we follow the following procedure for each of the symbols:
For the terminal '0' (i.e. where x = '0') this results in:
and for the terminal '1' (i.e. where x = '1') this results in:
and for the nonterminal E (i.e. where x = E) this results in:
and for the nonterminal B (i.e. where x = B) this results in:
Note that the closure does not add new items in all cases - in the new sets above, for example, there are no nonterminals following the dot. We continue this process until no more new item sets are found. For the item sets 1, 2, and 4 there will be no transitions since the dot is not in front of any symbol. For item set 3 we see that the dot is in front of the terminals '*' and '+'. For '*' the transition goes to:
and for '+' the transition goes to:
For item set 5 we have to consider the terminals '0' and '1' and the nonterminal B. For the terminals we see that the resulting closed item sets are equal to the already found item sets 1 and 2, respectively. For the nonterminal B the transition goes to:
For item set 6 we also have to consider the terminal '0' and '1' and the nonterminal B. As before, the resulting item sets for the terminals are equal to the already found item sets 1 and 2. For the nonterminal B the transition goes to:
These final item sets have no symbols beyond their dots so no more new item sets are added and we are finished. The finite automaton, with item sets as its states is shown below.
The transition table for the automaton now looks as follows:
The reader may verify that this results indeed in the action and goto table that were presented earlier on.
: they don't do any lookahead (that is, they look ahead zero symbols) before deciding which reduction to perform. A grammar that needs lookahead to disambiguate reductions would require a parse table row containing different reduce actions in different columns, and the above procedure is not capable of creating such rows.
Refinements to the LR(0) table construction procedure (such as SLR
and LALR
) are capable of constructing reduce actions that do not occupy entire rows. Therefore, they are capable of parsing more grammars than LR(0) parsers.
A small example of a non-LR(0) grammar with a shift-reduce conflict is:
One of the item sets we then find is:
There is a shift-reduce conflict in this item set because in the cell in the action table for this item set and the terminal '1' there will be both a shift action to state 1 and a reduce action with rule 2.
A small example of a non-LR(0) grammar with a reduce-reduce conflict is:
In this case we obtain the following item set:
There is a reduce-reduce conflict in this item set because in the cells in the action table for this item set there will be both a reduce action for rule 3 and one for rule 4.
Both examples above can be solved by letting the parser use the follow set (see LL parser
) of a nonterminal A to decide if it is going to use one of As rules for a reduction; it will only use the rule A → w for a reduction if the next symbol on the input stream is in the follow set of A. This solution results in so-called Simple LR parser
s.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, an LR parser is a parser that reads input from Left to right (as it would appear if visually displayed) and produces a Rightmost derivation. The term LR(k) parser is also used; where the k refers to the number of unconsumed "look ahead
Lookahead
Lookahead is a tool in algorithms for looking ahead a few more input items before making a cost effective decision at one stage of the algorithm.- Lookahead in search problems :...
" input symbols that are used in making parsing decisions. Usually k is 1 and the term LR parser is often intended to refer to this case.
LR parsing can handle a larger range of languages than LL parsing, and is also better at error reporting, i.e. it detects syntactic errors when the input does not conform to the grammar as soon as possible. This is in contrast to an LL(k) (or even worse, an LL(*) parser) which may defer error detection to a different branch of the grammar due to backtracking, often making errors harder to localize across disjunctions with long common prefixes.
LR parsers are difficult to produce by hand and they are usually constructed by a parser generator or a compiler-compiler
Compiler-compiler
A compiler-compiler or compiler generator is a tool that creates a parser, interpreter, or compiler from some form of formal description of a language and machine...
. Depending on how the parsing table is generated, these parsers can be called simple LR parser
Simple LR parser
An SLR parser will typically have more conflict states than an LALR parser. For real-world computer languages, an SLR parser is usually not adequate, but for student projects in a compiler class it is a good learning tool....
s (SLR), look-ahead LR parsers
LALR parser
In computer science, an LALR parser is a type of LR parser based on a finite-state-automata concept. The data structure used by an LALR parser is a pushdown automaton...
(LALR), or canonical LR parser
Canonical LR parser
A canonical LR parser or LR parser is an LR parser whose parsing tables are constructed in a similar way as with LR parsers except that the items in the item sets also contain a lookahead, i.e., a terminal that is expected by the parser after the right-hand side of the rule...
s. LALR parsers have more language recognition power than SLR parsers. Canonical LR parsers have more recognition power than LALR parsers.
Theory
LR parsing was invented by Donald Knuth in 1965 in a paper, "On the Translation of Languages from Left to Right".In this paper, Donald Knuth proves that
"LR(k) grammars can be efficiently parsed with an execution time essentially proportional to the length of string",
and that "A language can be generated by an LR(k) grammar if and only if it is deterministic, if and only if it can be generated by an LR(1) grammar" .
A deterministic context-free language
Deterministic context-free language
A deterministic context-free language is a formal language which is defined by a deterministic context-free grammar. The set of deterministic context-free languages is called DCFL and is identical to the set of languages accepted by a deterministic pushdown automaton.The set of deterministic...
is a language for which some LR(k) grammar exists. Every LR(k) grammar for k > 1 can be mechanically transformed into an LR(1) grammar for the same language, while an LR(0) grammar for the same language may not exist; the LR(0) languages are a proper subset of the deterministic ones.
LR parsing can be generalized as arbitrary context-free language parsing without a performance penalty, even for LR(k) grammars. Note that the parsing of non-LR(k) context-free grammars is an order of magnitude slower (cubic instead of quadratic in relation to the input length).
The syntax of many programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s are defined by a grammar that is LR(k) (where k is a small constant, usually 1), or close to being so, and for this reason LR parsers are often used by compiler
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
s to perform syntax analysis of source code
Source code
In computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
.
An LR parser can be created from a context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
by a program called a parser generator or hand written by a programmer. A context-free grammar is classified as LR(k) if there exists an LR(k) parser for it, as determined by the parser generator.
An LR parser is said to perform bottom-up parsing
Bottom-up parsing
Bottom-up parsing is a strategy for analyzing unknown information that attempts to identify the most fundamental units first, and then to infer higher-order structures from them...
because it attempts to deduce the top level grammar productions by building up from the leaves.
An LR parser is based on an algorithm which is driven by a parser table, a data structure which contains the syntax of the computer language being parsed. So the term LR parser actually refers to a class of parser that can process almost any programming language, as long as the parser table for a programming language is supplied. The parser table is created by a program called a parser generator.
Architecture of LR parsers

Recursive ascent parser
In computing, recursive ascent parsing is a technique for implementing an LALR parser which uses mutually-recursive functions rather than tables. Thus, the parser is directly encoded in the host language similar to recursive descent...
, a set of mutually-recursive functions for every grammar, much like a recursive descent parser
Recursive descent parser
A recursive descent parser is a top-down parser built from a set of mutually-recursive procedures where each such procedure usually implements one of the production rules of the grammar...
. Conventionally, however, LR parsers are presented and implemented as table-based stack machines in which the call stack
Call stack
In computer science, a call stack is a stack data structure that stores information about the active subroutines of a computer program. This kind of stack is also known as an execution stack, control stack, run-time stack, or machine stack, and is often shortened to just "the stack"...
of the underlying recursive program is explicitly manipulated.
A table
Parsing table
A parsing table is the part of a parser that makes decisions about how to treat input tokens in compiler development.- Overview :A parsing table is a table describing what action its parser should take when a given input comes while it is in a given state...
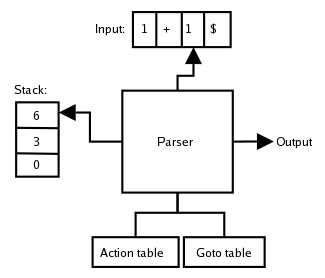
-driven bottom-up parser can be schematically presented as in Figure 1. The following describes a rightmost derivation by this parser.
General case
The parser is a state machine. It consists of:- an input bufferBuffer (computer science)In computer science, a buffer is a region of a physical memory storage used to temporarily hold data while it is being moved from one place to another. Typically, the data is stored in a buffer as it is retrieved from an input device or just before it is sent to an output device...
- a stackStack (data structure)In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
on which is stored a list of states it has been in - a goto table that prescribes to which new state it should move
- an action table that gives a grammar rule to apply given the current state and the current terminal in the input stream
- a set of CFLContext-free languageIn formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
rules
Since the LR parser reads input from left to right but needs to produce a rightmost derivation, it uses reductions, instead of derivations to process input. That is, the algorithm works by creating a "leftmost reduction" of the input. The end result, when reversed, will be a rightmost derivation.
The LR parsing algorithm works as follows:
- The stack is initialized with [0]. The current state will always be the state that is at the top of the stack.
- Given the current state and the current terminal on the input stream an action is looked up in the action table. There are four cases:
- a shift sn:
- the current terminal is removed from the input stream
- the state n is pushed onto the stack and becomes the current state
- a reduce rm:
- the number m is written to the output stream
- for every symbol in the right-hand side of rule m a state is removed from the stack (i. e. if the right-hand side of rule m consists of 3 symbols, 3 top states are removed from the stack)
- given the state that is then on top of the stack and the left-hand side of rule m a new state is looked up in the goto table and made the new current state by pushing it onto the stack
- an accept: the string is accepted
- no action: a syntax error is reported
- a shift sn:
- Step 2 is repeated until either the string is accepted or a syntax error is reported.
Concrete example
To explain its workings we will use the following small grammar whose start symbol is E:- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
and parse the following input:
- 1 + 1
Action and goto tables
The two LR(0) parsing tables for this grammar look as follows:| state | action | goto | |||||
| * | + | 0 | 1 | $ | E | B | |
| 0 | s1 | s2 | 3 | 4 | |||
| 1 | r4 | r4 | r4 | r4 | r4 | ||
| 2 | r5 | r5 | r5 | r5 | r5 | ||
| 3 | s5 | s6 | acc | ||||
| 4 | r3 | r3 | r3 | r3 | r3 | ||
| 5 | s1 | s2 | 7 | ||||
| 6 | s1 | s2 | 8 | ||||
| 7 | r1 | r1 | r1 | r1 | r1 | ||
| 8 | r2 | r2 | r2 | r2 | r2 | ||
The action table is indexed by a state of the parser and a terminal (including a special terminal $ that indicates the end of the input stream) and contains three types of actions:
- shift, which is written as 'sn' and indicates that the next state is n
- reduce, which is written as 'rm' and indicates that a reduction with grammar rule m should be performed
- accept, which is written as 'acc' and indicates that the parser accepts the string in the input stream.
The goto table is indexed by a state of the parser and a nonterminal and simply indicates what the next state of the parser will be if it has recognized a certain nonterminal. This table is important to find out the next state after every reduction. After a reduction, the next state is found by looking up the goto table entry for top of the stack (i.e. current state) and the reduced rule's LHS (i.e. non-terminal).
Parsing procedure
The table below illustrates each step in the process. Here the state refers to the element at the top of the stack (the right-most element), and the next action is determined by referring to the action table above. Also note that a $ is appended to the input string to denote the end of the stream.| State | Input Stream | Output Stream | Stack | Next Action |
|---|---|---|---|---|
| 0 | 1+1$ | [0] | Shift 2 | |
| 2 | +1$ | [0,2] | Reduce 5 | |
| 4 | +1$ | 5 | [0,4] | Reduce 3 |
| 3 | +1$ | 5,3 | [0,3] | Shift 6 |
| 6 | 1$ | 5,3 | [0,3,6] | Shift 2 |
| 2 | $ | 5,3 | [0,3,6,2] | Reduce 5 |
| 8 | $ | 5,3,5 | [0,3,6,8] | Reduce 2 |
| 3 | $ | 5,3,5,2 | [0,3] | Accept |
Walkthrough
The parser starts out with the stack containing just the initial state ('0'):- [0]
The first symbol from the input string that the parser sees is '1'. In order to find out what the next action is (shift, reduce, accept or error), the action table is indexed with the current state (remember that the "current state" is just whatever is on the top of the stack), which in this case is 0, and the current input symbol, which is '1'. The action table specifies a shift to state 2, and so state 2 is pushed onto the stack (again, remember that all the state information is in the stack, so "shifting to state 2" is the same thing as pushing 2 onto the stack). The resulting stack is
- [0 '1' 2]
where the top of the stack is 2. For the sake of explanation we also show the symbol (e.g., '1', B) that caused the transition to the next state, although strictly speaking it is not part of the stack.
In state 2 the action table says that regardless of what terminal we see on the input stream, we should do a reduction with grammar rule 5. If the table is correct, this means that the parser has just recognized the right-hand side of rule 5, which is indeed the case.
In this case we write 5 to the output stream, pop one state from the stack (since the right-hand side of the rule has one symbol), and push on the stack the state from the cell in the goto table for state 0 and B, i.e., state 4. The resulting stack is:
- [0 B 4]
However, in state 4 the action table says we should now do a reduction with rule 3. So we write 3 to the output stream, pop one state from the stack, and find the new state in the goto table for state 0 and E, which is state 3. The resulting stack:
- [0 E 3]
The next terminal that the parser sees is a '+' and according to the action table it should then go to state 6:
- [0 E 3 '+' 6]
Note that the resulting stack can be interpreted as the history of a finite state automaton that has just read a nonterminal E followed by a terminal '+'. The transition table of this automaton is defined by the shift actions in the action table and the goto actions in the goto table.
The next terminal is now '1' and this means that we perform a shift and go to state 2:
- [0 E 3 '+' 6 '1' 2]
Just as the previous '1' this one is reduced to B giving the following stack:
- [0 E 3 '+' 6 B 8]
Again note that the stack corresponds with a list of states of a finite automaton that has read a nonterminal E, followed by a '+' and then a nonterminal B. In state 8 we always perform a reduce with rule 2. Note that the top 3 states on the stack correspond with the 3 symbols in the right-hand side of rule 2.
- [0 E 3]
Finally, we read a '$' from the input stream which means that according to the action table (the current state is 3) the parser accepts the input string.
The rule numbers that will then have been written to the output stream will be [5, 3, 5, 2] which is indeed a rightmost derivation of the string "1 + 1" in reverse.
Items
The construction of these parsing tables is based on the notion of LR(0) items (simply called items here) which are grammar rules with a special dot added somewhere in the right-hand side. For example the rule E → E + B has the following four corresponding items:- E → • E + B
- E → E • + B
- E → E + • B
- E → E + B •
Rules of the form A → ε have only a single item A → •. The item E → E • + B, for example, indicates that the parser has recognized a string corresponding with E on the input stream and now expects to read a '+' followed by another string corresponding with B.
Item sets
It is usually not possible to characterize the state of the parser with a single item because it may not know in advance which rule it is going to use for reduction. For example if there is also a rule E → E * B then the items E → E • + B and E → E • * B will both apply after a string corresponding with E has been read. Therefore we will characterize the state of the parser by a set of items, in this case the set { E → E • + B, E → E • * B }.Extension of Item Set by expansion of non-terminals
An item with a dot before a nonterminal, such as E → E + • B, indicates that the parser expects to parse the nonterminal B next. To ensure the item set contains all possible rules the parser may be in the midst of parsing, it must include all items describing how B itself will be parsed. This means that if there are rules such as B → 1 and B → 0 then the item set must also include the items B → • 1 and B → • 0. In general this can be formulated as follows:- If there is an item of the form A → v • Bw in an item set and in the grammar there is a rule of the form B → w' then the item B → • w' should also be in the item set.
Closure of item sets
Thus, any set of items can be extended by recursively adding all the appropriate items until all nonterminals preceded by dots are accounted for. The minimal extension is called the closure of an item set and written as clos(I) where I is an item set. It is these closed item sets that we will take as the states of the parser, although only the ones that are actually reachable from the begin state will be included in the tables.Augmented grammar
Before we start determining the transitions between the different states, the grammar is always augmented with an extra rule- (0) S → E
where S is a new start symbol and E the old start symbol. The parser will use this rule for reduction exactly when it has accepted the input string.
For our example we will take the same grammar as before and augment it:
- (0) S → E
- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
It is for this augmented grammar that we will determine the item sets and the transitions between them.
Finding the reachable item sets and the transitions between them
The first step of constructing the tables consists of determining the transitions between the closed item sets. These transitions will be determined as if we are considering a finite automaton that can read terminals as well as nonterminals. The begin state of this automaton is always the closure of the first item of the added rule: S → • E:- Item set 0
- S → • E
- + E → • E * B
- + E → • E + B
- + E → • B
- + B → • 0
- + B → • 1
The boldfaced "+" in front of an item indicates the items that were added for the closure (not to be confused with the mathematical '+' operator which is a terminal). The original items without a "+" are called the kernel of the item set.
Starting at the begin state (S0) we will now determine all the states that can be reached from this state. The possible transitions for an item set can be found by looking at the symbols (terminals and nonterminals) we find right after the dots; in the case of item set 0 those symbols are the terminals '0' and '1' and the nonterminals E and B. To find the item set that each symbol x leads to we follow the following procedure for each of the symbols:
- Take the subset, S, of all items in the current item set where there is a dot in front of the symbol of interest, x.
- For each item in S, move the dot to the right of x.
- Close the resulting set of items.
For the terminal '0' (i.e. where x = '0') this results in:
- Item set 1
- B → 0 •
and for the terminal '1' (i.e. where x = '1') this results in:
- Item set 2
- B → 1 •
and for the nonterminal E (i.e. where x = E) this results in:
- Item set 3
- S → E •
- E → E • * B
- E → E • + B
and for the nonterminal B (i.e. where x = B) this results in:
- Item set 4
- E → B •
Note that the closure does not add new items in all cases - in the new sets above, for example, there are no nonterminals following the dot. We continue this process until no more new item sets are found. For the item sets 1, 2, and 4 there will be no transitions since the dot is not in front of any symbol. For item set 3 we see that the dot is in front of the terminals '*' and '+'. For '*' the transition goes to:
- Item set 5
- E → E * • B
- + B → • 0
- + B → • 1
and for '+' the transition goes to:
- Item set 6
- E → E + • B
- + B → • 0
- + B → • 1
For item set 5 we have to consider the terminals '0' and '1' and the nonterminal B. For the terminals we see that the resulting closed item sets are equal to the already found item sets 1 and 2, respectively. For the nonterminal B the transition goes to:
- Item set 7
- E → E * B •
For item set 6 we also have to consider the terminal '0' and '1' and the nonterminal B. As before, the resulting item sets for the terminals are equal to the already found item sets 1 and 2. For the nonterminal B the transition goes to:
- Item set 8
- E → E + B •
These final item sets have no symbols beyond their dots so no more new item sets are added and we are finished. The finite automaton, with item sets as its states is shown below.
The transition table for the automaton now looks as follows:
| Item Set | * | + | 0 | 1 | E | B |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| 1 | ||||||
| 2 | ||||||
| 3 | 5 | 6 | ||||
| 4 | ||||||
| 5 | 1 | 2 | 7 | |||
| 6 | 1 | 2 | 8 | |||
| 7 | ||||||
| 8 |
Constructing the action and goto tables
From this table and the found item sets we construct the action and goto table as follows:- the columns for nonterminals are copied to the goto table
- the columns for the terminals are copied to the action table as shift actions
- an extra column for '$' (end of input) is added to the action table that contains acc for every item set that contains S → E •.
- if an item set i contains an item of the form A → w • and A → w is rule m with m > 0 then the row for state i in the action table is completely filled with the reduce action rm.
The reader may verify that this results indeed in the action and goto table that were presented earlier on.
A note about LR(0) versus SLR and LALR parsing
Note that only step 4 of the above procedure produces reduce actions, and so all reduce actions must occupy an entire table row, causing the reduction to occur regardless of the next symbol in the input stream. This is why these are LR(0) parse tablesParsing table
A parsing table is the part of a parser that makes decisions about how to treat input tokens in compiler development.- Overview :A parsing table is a table describing what action its parser should take when a given input comes while it is in a given state...
: they don't do any lookahead (that is, they look ahead zero symbols) before deciding which reduction to perform. A grammar that needs lookahead to disambiguate reductions would require a parse table row containing different reduce actions in different columns, and the above procedure is not capable of creating such rows.
Refinements to the LR(0) table construction procedure (such as SLR
Simple LR parser
An SLR parser will typically have more conflict states than an LALR parser. For real-world computer languages, an SLR parser is usually not adequate, but for student projects in a compiler class it is a good learning tool....
and LALR
LALR parser
In computer science, an LALR parser is a type of LR parser based on a finite-state-automata concept. The data structure used by an LALR parser is a pushdown automaton...
) are capable of constructing reduce actions that do not occupy entire rows. Therefore, they are capable of parsing more grammars than LR(0) parsers.
Conflicts in the constructed tables
The automaton is constructed in such a way that it is guaranteed to be deterministic. However, when reduce actions are added to the action table it can happen that the same cell is filled with a reduce action and a shift action (a shift-reduce conflict) or with two different reduce actions (a reduce-reduce conflict). However, it can be shown that when this happens the grammar is not an LR(0) grammar.A small example of a non-LR(0) grammar with a shift-reduce conflict is:
- (1) E → 1 E
- (2) E → 1
One of the item sets we then find is:
- Item set 1
- E → 1 • E
- E → 1 •
- + E → • 1 E
- + E → • 1
There is a shift-reduce conflict in this item set because in the cell in the action table for this item set and the terminal '1' there will be both a shift action to state 1 and a reduce action with rule 2.
A small example of a non-LR(0) grammar with a reduce-reduce conflict is:
- (1) E → A 1
- (2) E → B 2
- (3) A → 1
- (4) B → 1
In this case we obtain the following item set:
- Item set 1
- A → 1 •
- B → 1 •
There is a reduce-reduce conflict in this item set because in the cells in the action table for this item set there will be both a reduce action for rule 3 and one for rule 4.
Both examples above can be solved by letting the parser use the follow set (see LL parser
LL parser
An LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
) of a nonterminal A to decide if it is going to use one of As rules for a reduction; it will only use the rule A → w for a reduction if the next symbol on the input stream is in the follow set of A. This solution results in so-called Simple LR parser
Simple LR parser
An SLR parser will typically have more conflict states than an LALR parser. For real-world computer languages, an SLR parser is usually not adequate, but for student projects in a compiler class it is a good learning tool....
s.
See also
- Canonical LRCanonical LR parserA canonical LR parser or LR parser is an LR parser whose parsing tables are constructed in a similar way as with LR parsers except that the items in the item sets also contain a lookahead, i.e., a terminal that is expected by the parser after the right-hand side of the rule...
- Deterministic context-free grammarDeterministic context-free grammarIn formal grammar theory, the deterministic context-free grammars are a proper subset of the context-free grammars. The deterministic context-free grammars are those a deterministic pushdown automaton can recognize...
- Look-Ahead LRLALR parserIn computer science, an LALR parser is a type of LR parser based on a finite-state-automata concept. The data structure used by an LALR parser is a pushdown automaton...
- Generalized LRGLR parserA GLR parser is an extension of an LR parser algorithm to handle nondeterministic and ambiguous grammars. First described in a 1984 paper by Masaru Tomita, it has also been referred to as a "parallel parser"...
- LL parserLL parserAn LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
- Simple LRSLR GrammarIn computer science, an SLR grammar is a class of formal grammar that can be parsed by a simple LR parser.- Definitions :A rule of the form B → y. within a state of a SLR automaton is said to be irreducible or in a reduce state because it has been completely expanded and is incapable of undergoing...
Further reading
- Chapman, Nigel P., LR Parsing: Theory and Practice, Cambridge University PressCambridge University PressCambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
, 1987. ISBN 0-521-30413-X - Pager, D., A Practical General Method for Constructing LR(k) Parsers. Acta Informatica 7, 249 - 268 (1977)
External links
- Parsing Simulator This simulator is used to generate parsing tables LR and to resolve the exercises of the book
- Internals of an LALR(1) parser generated by GNU Bison - Implementation issues

