Deterministic pushdown automaton
Encyclopedia
In automata theory
, a pushdown automaton
is a finite automaton with an additional stack
of symbols; its transitions can take the top symbol on the stack and depend on its value, and they can add new top symbols to the stack.
A deterministic pushdown automaton is effectively a particular type of pushdown automaton
, namely one that has at most one transition for the same combination of input symbol, state, and top stack symbol.
Technically however, the notion of determinism for pushdown automata is more complicated than for finite automata as the transition is determined by both state and top stack symbol. This means that if we omit the stack from a deterministic pushdown automaton we usually end up with a nondeterministic finite automaton.
The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow operations on other elements, and stack automata can recognize a strictly larger set of languages than pushdown automata.
A deterministic context-free language
is a language recognized by some deterministic pushdown automaton. Not all context-free languages are deterministic. This is unlike the situation for deterministic finite automata, which are also a subset of the nondeterministic finite automata but can recognize the same class of languages
(as demonstrated by the subset construction).
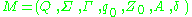
where
M is deterministic if it satisfies both the following conditions:
There are two possible acceptance criteria: acceptance by empty stack and acceptance by final state. The two are not equivalent for the deterministic pushdown automaton (although they are for the non-deterministic pushdown automaton). The languages accepted by empty stack are the languages that are accepted by final state, as well as have no word in the language that is the prefix of another word in the language.
Similarly, unlike the nondeterministic pushdown automaton, restricting the deterministic PDA to a single state reduces the class of languages accepted. The LL(1) languages are exactly those which can be recognized by single-state deterministic PDAs .
, with the only difference being that there is now only one computation for each input. For an automaton A, L(A) is the set of inputs such that there is a computation from the initial configuration until an accepting one.
As a consequence of the complementation it is decidable whether a deterministic PDA accepts all words over its input alphabet, by testing its complement for emptiness. This is not possible for context-free grammars (hence not for general PDA).
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
, a pushdown automaton
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
is a finite automaton with an additional stack
Stack (data structure)
In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
of symbols; its transitions can take the top symbol on the stack and depend on its value, and they can add new top symbols to the stack.
A deterministic pushdown automaton is effectively a particular type of pushdown automaton
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
, namely one that has at most one transition for the same combination of input symbol, state, and top stack symbol.
Technically however, the notion of determinism for pushdown automata is more complicated than for finite automata as the transition is determined by both state and top stack symbol. This means that if we omit the stack from a deterministic pushdown automaton we usually end up with a nondeterministic finite automaton.
The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow operations on other elements, and stack automata can recognize a strictly larger set of languages than pushdown automata.
A deterministic context-free language
Deterministic context-free language
A deterministic context-free language is a formal language which is defined by a deterministic context-free grammar. The set of deterministic context-free languages is called DCFL and is identical to the set of languages accepted by a deterministic pushdown automaton.The set of deterministic...
is a language recognized by some deterministic pushdown automaton. Not all context-free languages are deterministic. This is unlike the situation for deterministic finite automata, which are also a subset of the nondeterministic finite automata but can recognize the same class of languages
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
(as demonstrated by the subset construction).
Formal Definition
A (not necessarily deterministic) PDA M can be defined as a 7-tuple:where
is a finite set of states
is a finite set of input symbols
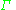is a finite set of stack symbols
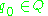is the start state
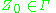is the starting stack symbol
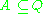, where 
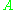is the set of accepting states
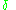is a transition function, where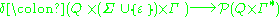
- where
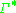means "a finite list (maybe empty) of elements of 
", 
denotes the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
, and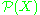
is the power set of a set 
.
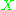M is deterministic if it satisfies both the following conditions:
- For any
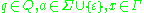, the set 
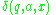has at most one element. - For any
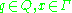, if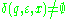 
, then 
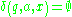for every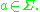 
There are two possible acceptance criteria: acceptance by empty stack and acceptance by final state. The two are not equivalent for the deterministic pushdown automaton (although they are for the non-deterministic pushdown automaton). The languages accepted by empty stack are the languages that are accepted by final state, as well as have no word in the language that is the prefix of another word in the language.
Similarly, unlike the nondeterministic pushdown automaton, restricting the deterministic PDA to a single state reduces the class of languages accepted. The LL(1) languages are exactly those which can be recognized by single-state deterministic PDAs .
Computation
The formal definition of the computation is the same as that of the pushdown automatonPushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
, with the only difference being that there is now only one computation for each input. For an automaton A, L(A) is the set of inputs such that there is a computation from the initial configuration until an accepting one.
Closure
Closure properties of deterministic context-free languages (accepted by deterministic PDA by final state) are drastically different from the context-free languages. As an example they are (effectively) closed under complementation, but not closed under union. To prove that the complement of a language accepted by a deterministic PDA is also accepted by a deterministic PDA is tricky. In principle one has to avoid infinite computations.As a consequence of the complementation it is decidable whether a deterministic PDA accepts all words over its input alphabet, by testing its complement for emptiness. This is not possible for context-free grammars (hence not for general PDA).