Structural proof theory
Encyclopedia
In mathematical logic
, structural proof theory is the subdiscipline of proof theory
that studies proof calculi that support a notion of analytic proof
.
for the sequent calculus
; the analytic proofs are those that are cut-free
. His natural deduction calculus also supports a notion of analytic proof, as was shown by Dag Prawitz
; the definition is slightly more complex — we say the analytic proofs are the normal forms, which are related to the notion of normal form in term rewriting.
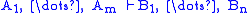, the commas to the left of the turnstile
are operators normally interpreted as conjunctions, those to the right as disjunctions, whilst the turnstile symbol itself is interpreted as an implication. However, it is important to note that there is a fundamental difference in behaviour between these operators and the logical connective
s they are interpreted by in the sequent calculus: the structural operators are used in every rule of the calculus, and are not considered when asking whether the subformula property applies. Furthermore, the logical rules go one way only: logical structure is introduced by logical rules, and cannot be eliminated once created, while structural operators can be introduced and eliminated in the course of a derivation.
The idea of looking at the syntactic features of sequents as special, non-logical operators is not old, and was forced by innovations in proof theory: when the structural operators are as simple as in Getzen's original sequent calculus there is little need to analyse them, but proof calculi of deep inference
such as display logic support structural operators as complex as the logical connectives, and demand sophisticated treatment.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, structural proof theory is the subdiscipline of proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
that studies proof calculi that support a notion of analytic proof
Analytic proof
In mathematical analysis, an analytical proof is a proof of a theorem in analysis that only makes use of methods from analysis, and which does not make use of results from geometry...
.
Analytic proof
The notion of analytic proof was introduced into proof theory by Gerhard GentzenGerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
for the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
; the analytic proofs are those that are cut-free
Cut-elimination theorem
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively...
. His natural deduction calculus also supports a notion of analytic proof, as was shown by Dag Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
; the definition is slightly more complex — we say the analytic proofs are the normal forms, which are related to the notion of normal form in term rewriting.
Structures and connectives
The term structure in structural proof theory comes from a technical notion introduced in the sequent calculus: the sequent calculus represents the judgement made at any stage of an inference using special, extra-logical operators which we call structural operators: in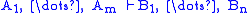, the commas to the left of the turnstileTurnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
are operators normally interpreted as conjunctions, those to the right as disjunctions, whilst the turnstile symbol itself is interpreted as an implication. However, it is important to note that there is a fundamental difference in behaviour between these operators and the logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s they are interpreted by in the sequent calculus: the structural operators are used in every rule of the calculus, and are not considered when asking whether the subformula property applies. Furthermore, the logical rules go one way only: logical structure is introduced by logical rules, and cannot be eliminated once created, while structural operators can be introduced and eliminated in the course of a derivation.
The idea of looking at the syntactic features of sequents as special, non-logical operators is not old, and was forced by innovations in proof theory: when the structural operators are as simple as in Getzen's original sequent calculus there is little need to analyse them, but proof calculi of deep inference
Deep inference
Deep inference names a general idea in structural proof theory that breaks with the classical sequent calculus by generalising the notion of structure to permit inference to occur in contexts of high structural complexity...
such as display logic support structural operators as complex as the logical connectives, and demand sophisticated treatment.