Self-verifying theories
Encyclopedia
Self-verifying theories are consistent first-order
systems of arithmetic
much weaker than Peano arithmetic that are capable of proving their own consistency
. Dan Willard was the first to investigate their properties, and he has described a family of such systems. According to Gödel's incompleteness theorem, these systems cannot contain the theory of Peano arithmetic, and in fact, not even the weak fragment of Robinson arithmetic
; nonetheless, they can contain strong theorems; for instance there are self-verifying systems capable of proving the consistency of Peano arithmetic.
In outline, the key to Willard's construction of his system is to formalise enough of the Gödel
machinery to talk about provability internally without being able to formalise diagonalisation
. Diagonalisation depends upon being able to prove that multiplication is a total function (and in the earlier versions of the result, addition also). Addition and multiplication are not function symbols of Willard's language; instead, subtraction and division are, with the addition and multiplication predicates being defined in terms of these. Here, one cannot prove the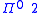
sentence
expressing totality of multiplication:
where
is the three-place predicate which stands for 
.
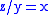When the operations are expressed in this way, provability of a given sentence can be encoded as an arithmetic sentence describing termination of an analytic tableaux. Provability of consistency can then simply be added as an axiom. The resulting system can be proven consistent by means of a relative consistency argument with respect to ordinary arithmetic.
We can add any true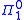
sentence of arithmetic to the theory and still remain consistent.
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
systems of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
much weaker than Peano arithmetic that are capable of proving their own consistency
Consistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
. Dan Willard was the first to investigate their properties, and he has described a family of such systems. According to Gödel's incompleteness theorem, these systems cannot contain the theory of Peano arithmetic, and in fact, not even the weak fragment of Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
; nonetheless, they can contain strong theorems; for instance there are self-verifying systems capable of proving the consistency of Peano arithmetic.
In outline, the key to Willard's construction of his system is to formalise enough of the Gödel
Godel
Godel or similar can mean:*Kurt Gödel , an Austrian logician, mathematician and philosopher*Gödel...
machinery to talk about provability internally without being able to formalise diagonalisation
Diagonal lemma
In mathematical logic, the diagonal lemma or fixed point theorem establishes the existence of self-referential sentences in certain formal theories of the natural numbers -- specifically those theories that are strong enough to represent all computable functions...
. Diagonalisation depends upon being able to prove that multiplication is a total function (and in the earlier versions of the result, addition also). Addition and multiplication are not function symbols of Willard's language; instead, subtraction and division are, with the addition and multiplication predicates being defined in terms of these. Here, one cannot prove the
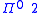sentenceArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
expressing totality of multiplication:
where
is the three-place predicate which stands for 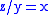.When the operations are expressed in this way, provability of a given sentence can be encoded as an arithmetic sentence describing termination of an analytic tableaux. Provability of consistency can then simply be added as an axiom. The resulting system can be proven consistent by means of a relative consistency argument with respect to ordinary arithmetic.
We can add any true
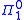sentence of arithmetic to the theory and still remain consistent.