
Reduced product
Encyclopedia
In model theory
, a branch of mathematical logic
, and in algebra
, the reduced product is a construction that generalizes both direct product
and ultraproduct
.
Let {Si | i ∈ I} be a family of structures
of the same signature
σ indexed by a set I, and let U be a filter
on I. The domain of the reduced product is the quotient of the Cartesian product
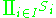
by a certain equivalence relation ~: two elements (ai) and (bi) of the Cartesian product are equivalent if
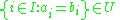
If U only contains I as an element, the equivalence relation is trivial, and the reduced product is just the original Cartesian product. If U is an ultrafilter
, the reduced product is an ultraproduct.
Operations from σ are interpreted on the reduced product by applying the operation pointwise. Relations are interpreted by
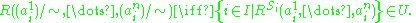
For example, if each structure is a vector space
, then the reduced product is a vector space with addition defined as (a + b)i = ai + bi and multiplication by a scalar c as (ca)i = c ai.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, and in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the reduced product is a construction that generalizes both direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
and ultraproduct
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
.
Let {Si | i ∈ I} be a family of structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
of the same signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ indexed by a set I, and let U be a filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
on I. The domain of the reduced product is the quotient of the Cartesian product
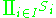
by a certain equivalence relation ~: two elements (ai) and (bi) of the Cartesian product are equivalent if
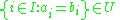
If U only contains I as an element, the equivalence relation is trivial, and the reduced product is just the original Cartesian product. If U is an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
, the reduced product is an ultraproduct.
Operations from σ are interpreted on the reduced product by applying the operation pointwise. Relations are interpreted by
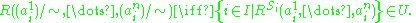
For example, if each structure is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, then the reduced product is a vector space with addition defined as (a + b)i = ai + bi and multiplication by a scalar c as (ca)i = c ai.

