Truth table
Encyclopedia
A truth table is a mathematical table
used in logic
—specifically in connection with Boolean algebra, boolean functions, and propositional calculus
—to compute the functional values of logical expression
s on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton, 2001). In particular, truth tables can be used to tell whether a propositional expression is true for all legitimate input values, that is, logically valid
.
Practically, a truth table is composed of one column for each input variable (for example, A and B), and one final column for all of the possible results of the logical operation that the table is meant to represent (for example, A XOR B). Each row of the truth table therefore contains one possible configuration of the input variables (for instance, A=true B=false), and the result of the operation for those values. See the examples below for further clarification. Ludwig Wittgenstein
is often credited with their invention in the Tractatus Logico-Philosophicus
.
is an operation on one logical value
, typically the value of a proposition
, that produces a value of true if its operand is true and a value of false if its operand is false.
The truth table for the logical identity operator is as follows:
, typically the value of a proposition
, that produces a value of true if its operand is false and a value of false if its operand is true.
The truth table for NOT p (also written as ¬p, Np, Fpq, or ~p) is as follows:
where T = true and F = false.
Key:
Logical operators can also be visualized using Venn diagram
s.
is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if both of its operands are true.
The truth table for p AND q (also written as p ∧ q, Kpq, p & q, or p
q) is as follows:
In ordinary language terms, if both p and q are true, then the conjunction p ∧ q is true. For all other assignments of logical values to p and to q the conjunction p ∧ q is false.
It can also be said that if p, then p ∧ q is q, otherwise p ∧ q is p.
is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if at least one of its operands is true.
The truth table for p OR q (also written as p ∨ q, Apq, p || q, or p + q) is as follows:
Stated in English, if p, then p ∨ q is p, otherwise p ∨ q is q.
s, typically the values of two proposition
s, that produces a value of false just in the singular case the first operand is true and the second operand is false.
The truth table associated with the material conditional if p then q (symbolized as p → q) and the logical implication p implies q (symbolized as p ⇒ q, or Cpq) is as follows:
It may also be useful to note that p → q is equivalent to ¬p ∨ q.
(also known as biconditional) is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if both operands are false or both operands are true.
The truth table for p XNOR q (also written as p ↔ q , Epq, p = q, or p ≡ q) is as follows:
So p EQ q is true if p and q have the same truth value (both true or both false), and false if they have different truth values.
is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if one but not both of its operands is true.
The truth table for p XOR q (also written as p ⊕ q, Jpq, or p ≠ q) is as follows:
For two propositions, XOR can also be written as (p = 1 ∧ q = 0)∨ (p = 0 ∧ q = 1).
s, typically the values of two proposition
s, that produces a value of false if both of its operands are true. In other words, it produces a value of true if at least one of its operands is false.
The truth table for p NAND q (also written as p ↑ q, Dpq, or p | q) is as follows:
It is frequently useful to express a logical operation as a compound operation, that is, as an operation that is built up or composed from other operations. Many such compositions are possible, depending on the operations that are taken as basic or "primitive" and the operations that are taken as composite or "derivative".
In the case of logical NAND, it is clearly expressible as a compound of NOT and AND.
The negation of a conjunction: ¬(p ∧ q), and the disjunction of negations: (¬p) ∨ (¬q) can be tabulated as follows:
is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if both of its operands are false. In other words, it produces a value of false if at least one of its operands is true. ↓ is also known as the Peirce arrow after its inventor, Charles Sanders Peirce, and is a Sole sufficient operator.
The truth table for p NOR q (also written as p ↓ q, Xpq, or p ⊥ q) is as follows:
The negation of a disjunction ¬(p ∨ q), and the conjunction of negations (¬p) ∧ (¬q) can be tabulated as follows:
Inspection of the tabular derivations for NAND and NOR, under each assignment of logical values to the functional arguments p and q, produces the identical patterns of functional values for ¬(p ∧ q) as for (¬p) ∨ (¬q), and for ¬(p ∨ q) as for (¬p) ∧ (¬q). Thus the first and second expressions in each pair are logically equivalent, and may be substituted for each other in all contexts that pertain solely to their logical values.
This equivalence is one of De Morgan's laws.
s. For example, consider the following truth table:
This demonstrates the fact that p → q is logically equivalent to ¬p ∨ q.
Key:
biconditional or "if-and-only-if"
is logically equivalent
to
: XNOR (exclusive nor).
Logical operators can also be visualized using Venn diagram
s.
uses this condensed truth table notation:
This notation is useful especially if the operations are commutative, although one can additionally specify that the rows are the first operand and the columns are the second operand. This condensed notation is particularly useful in discussing multi-valued extensions of logic, as it significantly cuts down on combinatoric explosion of the number of rows otherwise needed. It also provides for quickly recognizable characteristic "shape" of the distribution of the values in the table which can assist the reader in grasping the rules more quickly.
. For an n-input LUT, the truth table will have 2^n values (or rows in the above tabular format), completely specifying a boolean function for the LUT. By representing each boolean value as a bit
in a binary number
, truth table values can be efficiently encoded as integer
values in electronic design automation (EDA)
software. For example, a 32-bit integer can encode the truth table for a LUT with up to 5 inputs.
When using an integer representation of a truth table, the output value of the LUT can be obtained by calculating a bit index k based on the input values of the LUT, in which case the LUT's output value is the kth bit of the integer. For example, to evaluate the output value of a LUT given an array of n boolean input values, the bit index of the truth table's output value can be computed as follows: if the ith input is true, let Vi = 1, else let Vi = 0. Then the kth bit of the binary representation of the truth table is the LUT's output value, where k = V0*2^0 + V1*2^1 + V2*2^2 + ... + Vn*2^n.
Truth tables are a simple and straightforward way to encode boolean functions, however given the exponential growth
in size as the number of inputs increase, they are not suitable for functions with a large number of inputs. Other representations which are more memory efficient are text equations and binary decision diagram
s.
This truth table is read left to right:
Note that this table does not describe the logic operations necessary to implement this operation, rather it simply specifies the function of inputs to output values.
In this case it can only be used for very simple inputs and outputs, such as 1's and 0's, however if the number of types of values one can have on the inputs increases, the size of the truth table will increase.
For instance, in an addition operation, one needs two operands, A and B. Each can have one of two values, zero or one. The number of combinations of these two values is 2x2, or four. So the result is four possible outputs of C and R. If one was to use base 3, the size would increase to 3x3, or nine possible outputs.
The first "addition" example above is called a half-adder. A full-adder is when the carry from the previous operation is provided as input to the next adder. Thus, a truth table of eight rows would be needed to describe a full adder's logic:
Mathematical table
Before calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
used in logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
—specifically in connection with Boolean algebra, boolean functions, and propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
—to compute the functional values of logical expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
s on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton, 2001). In particular, truth tables can be used to tell whether a propositional expression is true for all legitimate input values, that is, logically valid
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
.
Practically, a truth table is composed of one column for each input variable (for example, A and B), and one final column for all of the possible results of the logical operation that the table is meant to represent (for example, A XOR B). Each row of the truth table therefore contains one possible configuration of the input variables (for instance, A=true B=false), and the result of the operation for those values. See the examples below for further clarification. Ludwig Wittgenstein
Ludwig Wittgenstein
Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...
is often credited with their invention in the Tractatus Logico-Philosophicus
Tractatus Logico-Philosophicus
The Tractatus Logico-Philosophicus is the only book-length philosophical work published by the Austrian philosopher Ludwig Wittgenstein in his lifetime. It was an ambitious project: to identify the relationship between language and reality and to define the limits of science...
.
Logical identity
Logical identityIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is an operation on one logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
, typically the value of a proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
, that produces a value of true if its operand is true and a value of false if its operand is false.
The truth table for the logical identity operator is as follows:
| p | p |
|---|---|
| T | T |
| F | F |
Logical negation
Logical negation is an operation on one logical valueLogical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
, typically the value of a proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
, that produces a value of true if its operand is false and a value of false if its operand is true.
The truth table for NOT p (also written as ¬p, Np, Fpq, or ~p) is as follows:
| p | ¬p |
|---|---|
| T | F |
| F | T |
Truth table for all binary logical operators
Here is a truth table giving definitions of all 16 of the possible truth functions of 2 binary variables (P,Q are thus boolean variables):| P | Q | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | F | F | F | F | F | F | F | F | T | T | T | T | T | T | T | T | ||
| T | F | F | F | F | F | T | T | T | T | F | F | F | F | T | T | T | T | ||
| F | T | F | F | T | T | F | F | T | T | F | F | T | T | F | F | T | T | ||
| F | F | F | T | F | T | F | T | F | T | F | T | F | T | F | T | F | T |
where T = true and F = false.
Key:
| 0 | Opq | xand | false | Contradiction Contradiction In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other... |
|---|---|---|---|---|
| 1 | Xpq | NOR | ↓ | Logical NOR Logical NOR In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false... |
| 2 | Mpq | Xq | Converse nonimplication | |
| 3 | Fpq | Np | ¬p | Negation Negation In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified... |
| 4 | Lpq | Xp | ↛ | Material nonimplication Material nonimplication Material nonimplication or abjunction is the negation of implication. That is to say that for any two propositions P and Q, if P does not imply Q, then P is the material nonimplication of Q.... |
| 5 | Gpq | Nq | ¬q | Negation |
| 6 | Jpq | XOR | ⊕ | Exclusive disjunction Exclusive disjunction The logical operation exclusive disjunction, also called exclusive or , is a type of logical disjunction on two operands that results in a value of true if exactly one of the operands has a value of true... |
| 7 | Dpq | NAND | ↑ | Logical NAND |
| 8 | Kpq | AND | ∧ | Logical conjunction Logical conjunction In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false.... |
| 9 | Epq | XNOR | If and only if If and only if In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements.... |
Logical biconditional Logical biconditional In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion... |
| 10 | Hpq | q | Projection function | |
| 11 | Cpq | XNp | if/then | Material implication |
| 12 | Ipq | p | Projection function | |
| 13 | Bpq | XNq | then/if | Converse implication Converse implication Converse implication is the converse of implication. That is to say; that for any two propositions P and Q, if Q implies P, then P is the converse implication of Q.It may take the following forms:-Truth table:The truth table of A⊂B-Venn diagram:... |
| 14 | Apq | OR | ∨ | Logical disjunction Logical disjunction In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are... |
| 15 | Vpq | xnand | true | Tautology Tautology (logic) In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense... |
Logical operators can also be visualized using Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s.
Logical conjunction
Logical conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if both of its operands are true.
The truth table for p AND q (also written as p ∧ q, Kpq, p & q, or p
q) is as follows:| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
In ordinary language terms, if both p and q are true, then the conjunction p ∧ q is true. For all other assignments of logical values to p and to q the conjunction p ∧ q is false.
It can also be said that if p, then p ∧ q is q, otherwise p ∧ q is p.
Logical disjunction
Logical disjunctionLogical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if at least one of its operands is true.
The truth table for p OR q (also written as p ∨ q, Apq, p || q, or p + q) is as follows:
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Stated in English, if p, then p ∨ q is p, otherwise p ∨ q is q.
Logical implication
Logical implication and the material conditional are both associated with an operation on two logical valueLogical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of false just in the singular case the first operand is true and the second operand is false.
The truth table associated with the material conditional if p then q (symbolized as p → q) and the logical implication p implies q (symbolized as p ⇒ q, or Cpq) is as follows:
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
It may also be useful to note that p → q is equivalent to ¬p ∨ q.
Logical equality
Logical equalityLogical equality
Logical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus...
(also known as biconditional) is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if both operands are false or both operands are true.
The truth table for p XNOR q (also written as p ↔ q , Epq, p = q, or p ≡ q) is as follows:
| p | q | p ≡ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
So p EQ q is true if p and q have the same truth value (both true or both false), and false if they have different truth values.
Exclusive disjunction
Exclusive disjunctionExclusive disjunction
The logical operation exclusive disjunction, also called exclusive or , is a type of logical disjunction on two operands that results in a value of true if exactly one of the operands has a value of true...
is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if one but not both of its operands is true.
The truth table for p XOR q (also written as p ⊕ q, Jpq, or p ≠ q) is as follows:
| p | q | p ⊕ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
For two propositions, XOR can also be written as (p = 1 ∧ q = 0)∨ (p = 0 ∧ q = 1).
Logical NAND
The logical NAND is an operation on two logical valueLogical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of false if both of its operands are true. In other words, it produces a value of true if at least one of its operands is false.
The truth table for p NAND q (also written as p ↑ q, Dpq, or p | q) is as follows:
| p | q | p ↑ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
It is frequently useful to express a logical operation as a compound operation, that is, as an operation that is built up or composed from other operations. Many such compositions are possible, depending on the operations that are taken as basic or "primitive" and the operations that are taken as composite or "derivative".
In the case of logical NAND, it is clearly expressible as a compound of NOT and AND.
The negation of a conjunction: ¬(p ∧ q), and the disjunction of negations: (¬p) ∨ (¬q) can be tabulated as follows:
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | (¬p) ∨ (¬q) |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
Logical NOR
The logical NORLogical NOR
In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false...
is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if both of its operands are false. In other words, it produces a value of false if at least one of its operands is true. ↓ is also known as the Peirce arrow after its inventor, Charles Sanders Peirce, and is a Sole sufficient operator.
The truth table for p NOR q (also written as p ↓ q, Xpq, or p ⊥ q) is as follows:
| p | q | p ↓ q |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
The negation of a disjunction ¬(p ∨ q), and the conjunction of negations (¬p) ∧ (¬q) can be tabulated as follows:
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | (¬p) ∧ (¬q) |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
Inspection of the tabular derivations for NAND and NOR, under each assignment of logical values to the functional arguments p and q, produces the identical patterns of functional values for ¬(p ∧ q) as for (¬p) ∨ (¬q), and for ¬(p ∨ q) as for (¬p) ∧ (¬q). Thus the first and second expressions in each pair are logically equivalent, and may be substituted for each other in all contexts that pertain solely to their logical values.
This equivalence is one of De Morgan's laws.
Applications
Truth tables can be used to prove many other logical equivalenceLogical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
s. For example, consider the following truth table:
| p | q | ¬p | ¬p ∨ q | p → q |
|---|---|---|---|---|
| T | T | F | T | T |
| T | F | F | F | F |
| F | T | T | T | T |
| F | F | T | T | T |
This demonstrates the fact that p → q is logically equivalent to ¬p ∨ q.
Truth table for most commonly used logical operators
Here is a truth table giving definitions of the most commonly used 6 of the 16 possible truth functions of 2 binary variables (P,Q are thus boolean variables):  |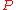
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|
| T | T | T | T | F | T | T | T | T |
| T | F | F | T | T | F | F | T | F |
| F | T | F | T | T | F | T | F | F |
| F | F | F | F | F | T | T | T | T |
Key:
- T = true, F = false
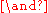= ANDLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
(logical conjunction)
= ORLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
(logical disjunction)
= XOR (exclusive or) 
= XNOR (exclusive nor)
= conditional "if-then"
= conditional "(then)-if"
biconditional or "if-and-only-if"If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to
: XNOR (exclusive nor).Logical operators can also be visualized using Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s.
Condensed truth tables for binary operators
For binary operators, a condensed form of truth table is also used, where the row headings and the column headings specify the operands and the table cells specify the result. For example Boolean logicBoolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
uses this condensed truth table notation:
EWLINE
|
EWLINE
|
This notation is useful especially if the operations are commutative, although one can additionally specify that the rows are the first operand and the columns are the second operand. This condensed notation is particularly useful in discussing multi-valued extensions of logic, as it significantly cuts down on combinatoric explosion of the number of rows otherwise needed. It also provides for quickly recognizable characteristic "shape" of the distribution of the values in the table which can assist the reader in grasping the rules more quickly.
Truth tables in digital logic
Truth tables are also used to specify the functionality of hardware look-up tables (LUTs) in digital logic circuitryDigital circuit
Digital electronics represent signals by discrete bands of analog levels, rather than by a continuous range. All levels within a band represent the same signal state...
. For an n-input LUT, the truth table will have 2^n values (or rows in the above tabular format), completely specifying a boolean function for the LUT. By representing each boolean value as a bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
in a binary number
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, truth table values can be efficiently encoded as integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values in electronic design automation (EDA)
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
software. For example, a 32-bit integer can encode the truth table for a LUT with up to 5 inputs.
When using an integer representation of a truth table, the output value of the LUT can be obtained by calculating a bit index k based on the input values of the LUT, in which case the LUT's output value is the kth bit of the integer. For example, to evaluate the output value of a LUT given an array of n boolean input values, the bit index of the truth table's output value can be computed as follows: if the ith input is true, let Vi = 1, else let Vi = 0. Then the kth bit of the binary representation of the truth table is the LUT's output value, where k = V0*2^0 + V1*2^1 + V2*2^2 + ... + Vn*2^n.
Truth tables are a simple and straightforward way to encode boolean functions, however given the exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
in size as the number of inputs increase, they are not suitable for functions with a large number of inputs. Other representations which are more memory efficient are text equations and binary decision diagram
Binary decision diagram
In the field of computer science, a binary decision diagram or branching program, like a negation normal form or a propositional directed acyclic graph , is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed...
s.
Applications of truth tables in digital electronics
In digital electronics (and computer science, fields of engineering derived from applied logic and math), truth tables can be used to reduce basic boolean operations to simple correlations of inputs to outputs, without the use of logic gates or code. For example, a binary addition can be represented with the truth table:
A B | C R
1 1 | 1 0
1 0 | 0 1
0 1 | 0 1
0 0 | 0 0
where
A = First Operand
B = Second Operand
C = Carry
R = Result
This truth table is read left to right:
- Value pair (A,B) equals value pair (C,R).
- Or for this example, A plus B equal result R, with the Carry C.
Note that this table does not describe the logic operations necessary to implement this operation, rather it simply specifies the function of inputs to output values.
In this case it can only be used for very simple inputs and outputs, such as 1's and 0's, however if the number of types of values one can have on the inputs increases, the size of the truth table will increase.
For instance, in an addition operation, one needs two operands, A and B. Each can have one of two values, zero or one. The number of combinations of these two values is 2x2, or four. So the result is four possible outputs of C and R. If one was to use base 3, the size would increase to 3x3, or nine possible outputs.
The first "addition" example above is called a half-adder. A full-adder is when the carry from the previous operation is provided as input to the next adder. Thus, a truth table of eight rows would be needed to describe a full adder's logic:
A B C* | C R
0 0 0 | 0 0
0 1 0 | 0 1
1 0 0 | 0 1
1 1 0 | 1 0
0 0 1 | 0 1
0 1 1 | 1 0
1 0 1 | 1 0
1 1 1 | 1 1
Same as previous, but..
C* = Carry from previous adder
See also
Related topics- Boolean domainBoolean domainIn mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
- Boolean-valued functionBoolean-valued functionA boolean-valued function, in some usages is a predicate or a proposition, is a function of the type f : X → B, where X is an arbitrary set and where B is a boolean domain....
- Excitation tableExcitation tableIn electronics design, an excitation table shows the minimum inputs that are necessary to generate a particular next state when the current state is known...
- Espresso heuristic logic minimizer
- Functional completeness
- First-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
- Karnaugh maps
- Logical connectiveLogical connectiveIn logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
- Logical graphLogical graphA logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
- Method of analytic tableauxMethod of analytic tableauxIn proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulas of first-order logic. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure...
- Multigrade operatorMultigrade operatorIn logic and mathematics, a multigrade operator \Omega is a parametric operator with parameter k in the set N of non-negative integers....
- Parametric operator
- Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
- Sole sufficient operator
Further reading
- Bocheński, Józef Maria (1959), A Précis of Mathematical Logic, translated from the French and German editions by Otto Bird, D. Reidel, Dordrecht, South Holland.
- Enderton, H. (2001). A Mathematical Introduction to Logic, second edition, Harcourt Academic Press. ISBN 0-12-238452-0
- Quine, W.V. (1982), Methods of Logic, 4th edition, Harvard University Press, Cambridge, MA.