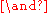Logical biconditional
Encyclopedia
In logic
and mathematics
, the logical biconditional (sometimes known as the material biconditional) is the logical connective
of two statements asserting "p if and only if
q", where q is a hypothesis
(or antecedent) and p is a conclusion (or consequent). The operator is denoted using a doubleheaded arrow (↔), a prefixed E (Epq), an equality sign (=), an equivalence sign (≡), or EQV. It is logically equivalent to (p → q) ∧ (q → p), or the XNOR (exclusive nor) boolean operator. It is equivalent to "(not p or q) and (not q or p)". It is also logically equivalent to "(p and q) or (not p and not q)", meaning "both or neither".
The only difference from material conditional
is the case when the hypothesis is false but the conclusion is true. In that case, in the conditional, the result is true, yet in the biconditional the result is false.
In the conceptual interpretation, a = b means "All a 's are b 's and all b 's are a 's"; in other words, the sets a and b coincide: they are identical. This does not mean that the concepts have the same meaning. Examples: "triangle" and "trilateral", "equiangular triangle" and "equilateral triangle". The antecedent is the subject and the consequent is the predicate of a universal affirmative
proposition
.
In the propositional interpretation, a ⇔ b means that a implies b and b implies a; in other words, that the propositions are equivalent, that is to say, either true or false at the same time. This does not mean that they have the same meaning. Example
: "The triangle ABC has two equal sides", and "The triangle ABC has two equal angles". The antecedent is the premise or the cause and the consequent is the consequence. When an implication is translated by a hypothetical (or conditional) judgment the antecedent is called the hypothesis (or the condition) and the consequent is called the thesis.
A common way of demonstrating a biconditional is to use its equivalence to the conjunction of two converse conditional
s, demonstrating these separately.
When both members of the biconditional are propositions, it can be separated into two conditionals, of which one is called a theorem and the other its reciprocal. Thus whenever a theorem and its reciprocal are true we have a biconditional. A simple theorem gives rise to an implication whose antecedent is the hypothesis and whose consequent is the thesis of the theorem.
It is often said that the hypothesis is the sufficient condition of the thesis, and the
thesis the necessary condition of the hypothesis; that is to say, it is sufficient that the hypothesis be true for the thesis to be true; while it is necessary that the thesis be true for the hypothesis to be true also. When a theorem and its reciprocal are true we say that its hypothesis is the necessary and sufficient condition of the thesis; that is to say, that it is at the same time both cause and consequence.
(also known as biconditional) is an operation on two logical value
s, typically the values of two proposition
s, that produces a value of true if and only if both operands are false or both operands are true.
(also written as A ≡ B, A = B, or A EQ B) is as follows:
More than two statements combined by
are ambiguous:
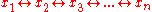may be meant as 
,
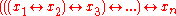or may be used to say that all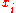
are together true or together false: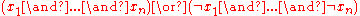 
Only for zero or two arguments this is the same.
The following truth tables show the same bit pattern only in the line with no argument and in the lines with two arguments:
The left Venn diagram below, and the lines (AB ) in these matrices represent the same operation.
for and
).
: yes
associativity
: yes
distributivity
: with no binary function, not even with itself
idempotency: no
monotonicity: no
truth-preserving: yes
When all inputs are true, the output is true.
falsehood-preserving: no
When all inputs are false, the output is not false.
Walsh spectrum
: (2,0,0,2)
Nonlinearity: 0 (the function is linear)
allows you to infer that, if B follows from A, and A follows from B, then A if and only if
B.
For example, from the statements "if I'm breathing, then I'm alive" and "if I'm alive, then I'm breathing", it can be inferred that "I'm breathing if and only if I'm alive".
B → A
A → B
∴ A ↔ B
from a biconditional: if ( A ↔ B ) is true, then one may infer one direction of the biconditional, ( A → B ) and ( B → A ).
For example, if it's true that I'm breathing if and only if
I'm alive, then it's true that if I'm breathing, I'm alive; likewise, it's true that if I'm alive, I'm breathing.
Formally:
( A ↔ B )
∴ ( A → B )
also
( A ↔ B )
∴ ( B → A )
For example, "I'll buy you an ice cream if you pass the exam" may be meant as a biconditional, since the speaker doesn't intend a valid outcome to be buying the ice cream whether or not you pass the exam (as in a conditional). However, "it is cloudy if it is raining" is not meant as a biconditional, since it can be cloudy while not raining.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the logical biconditional (sometimes known as the material biconditional) is the logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
of two statements asserting "p if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
q", where q is a hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
(or antecedent) and p is a conclusion (or consequent). The operator is denoted using a doubleheaded arrow (↔), a prefixed E (Epq), an equality sign (=), an equivalence sign (≡), or EQV. It is logically equivalent to (p → q) ∧ (q → p), or the XNOR (exclusive nor) boolean operator. It is equivalent to "(not p or q) and (not q or p)". It is also logically equivalent to "(p and q) or (not p and not q)", meaning "both or neither".
The only difference from material conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
is the case when the hypothesis is false but the conclusion is true. In that case, in the conditional, the result is true, yet in the biconditional the result is false.
In the conceptual interpretation, a = b means "All a 's are b 's and all b 's are a 's"; in other words, the sets a and b coincide: they are identical. This does not mean that the concepts have the same meaning. Examples: "triangle" and "trilateral", "equiangular triangle" and "equilateral triangle". The antecedent is the subject and the consequent is the predicate of a universal affirmative
Affirmative
Affirmative can mean:*Pertaining to truth*Pertaining to an assertion*An answer that shows agreement or acceptance: see yes*Affirmative , the team which affirms the resolution*Affirmative action...
proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
.
In the propositional interpretation, a ⇔ b means that a implies b and b implies a; in other words, that the propositions are equivalent, that is to say, either true or false at the same time. This does not mean that they have the same meaning. Example
Pons asinorum
Pons asinorum is the name given to Euclid's fifth proposition in Book 1 of his Elements of geometry, also known as the theorem on isosceles triangles. It states that the angles opposite the equal sides of an isosceles triangle are equal...
: "The triangle ABC has two equal sides", and "The triangle ABC has two equal angles". The antecedent is the premise or the cause and the consequent is the consequence. When an implication is translated by a hypothetical (or conditional) judgment the antecedent is called the hypothesis (or the condition) and the consequent is called the thesis.
A common way of demonstrating a biconditional is to use its equivalence to the conjunction of two converse conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
s, demonstrating these separately.
When both members of the biconditional are propositions, it can be separated into two conditionals, of which one is called a theorem and the other its reciprocal. Thus whenever a theorem and its reciprocal are true we have a biconditional. A simple theorem gives rise to an implication whose antecedent is the hypothesis and whose consequent is the thesis of the theorem.
It is often said that the hypothesis is the sufficient condition of the thesis, and the
thesis the necessary condition of the hypothesis; that is to say, it is sufficient that the hypothesis be true for the thesis to be true; while it is necessary that the thesis be true for the hypothesis to be true also. When a theorem and its reciprocal are true we say that its hypothesis is the necessary and sufficient condition of the thesis; that is to say, that it is at the same time both cause and consequence.
Definition
Logical equalityLogical equality
Logical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus...
(also known as biconditional) is an operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if and only if both operands are false or both operands are true.
Truth table
The truth table for (also written as A ≡ B, A = B, or A EQ B) is as follows:| INPUT | OUTPUT | |
| A | B | A  B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
More than two statements combined by
are ambiguous: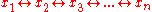 may be meant as 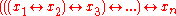,or may be used to say that all
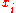are together true or together false: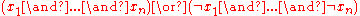 Only for zero or two arguments this is the same.
The following truth tables show the same bit pattern only in the line with no argument and in the lines with two arguments:
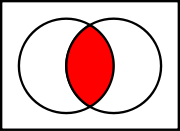
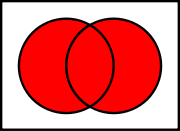
The left Venn diagram below, and the lines (AB ) in these matrices represent the same operation.
Venn diagrams
Red areas stand for true (as in for andLogical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
).
EWLINE
|
EWLINE
|
EWLINE
|
Properties
commutativityCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
: yes
 |
 |
 |
 |
associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
: yes
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
: with no binary function, not even with itself
idempotency: no
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
monotonicity: no
 |
 |
 |
 |
 |
||
 |
 |
 |
truth-preserving: yes
When all inputs are true, the output is true.
 |
 |
 |
|
 |
falsehood-preserving: no
When all inputs are false, the output is not false.
 |
 |
 |
 |
 |
Walsh spectrum
Hadamard transform
The Hadamard transform is an example of a generalized class of Fourier transforms...
: (2,0,0,2)
Nonlinearity: 0 (the function is linear)
Rules of Inference
Like all connectives in first-order logic, the biconditional has rules of inference that govern its use in formal proofs.Biconditional Introduction
Biconditional introductionBiconditional introduction
In mathematical logic, biconditional introduction is the rule of inference that, if B follows from A, and A follows from B, then A if and only if B....
allows you to infer that, if B follows from A, and A follows from B, then A if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
B.
For example, from the statements "if I'm breathing, then I'm alive" and "if I'm alive, then I'm breathing", it can be inferred that "I'm breathing if and only if I'm alive".
B → A
A → B
∴ A ↔ B
Biconditional Elimination
Biconditional elimination allows one to infer a conditionalMaterial conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
from a biconditional: if ( A ↔ B ) is true, then one may infer one direction of the biconditional, ( A → B ) and ( B → A ).
For example, if it's true that I'm breathing if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
I'm alive, then it's true that if I'm breathing, I'm alive; likewise, it's true that if I'm alive, I'm breathing.
Formally:
( A ↔ B )
∴ ( A → B )
also
( A ↔ B )
∴ ( B → A )
Colloquial usage
One unambiguous way of stating a biconditional in plain English is of the form "b if a and a if b". Another is "a if and only if b". Slightly more formally, one could say "b implies a and a implies b". The plain English "if'" may sometimes be used as a biconditional. One must weigh context heavily.For example, "I'll buy you an ice cream if you pass the exam" may be meant as a biconditional, since the speaker doesn't intend a valid outcome to be buying the ice cream whether or not you pass the exam (as in a conditional). However, "it is cloudy if it is raining" is not meant as a biconditional, since it can be cloudy while not raining.
See also
- If and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
- Logical equivalenceLogical equivalenceIn logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
- Logical equalityLogical equalityLogical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus...
- XNOR gateXNOR gateThe XNOR gate is a digital logic gate whose function is the inverse of the exclusive OR gate. The two-input version implements logical equality, behaving according to the truth table to the right. A HIGH output results if both of the inputs to the gate are the same...
- Biconditional eliminationBiconditional eliminationBiconditional elimination allows one to infer a conditional from a biconditional: if is true, then one may infer either direction of the biconditional, and ....
- Biconditional introductionBiconditional introductionIn mathematical logic, biconditional introduction is the rule of inference that, if B follows from A, and A follows from B, then A if and only if B....