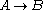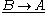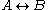In mathematical logic

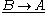
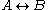
Mathematical logic

Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

, biconditional introduction is the rule of inference

Rule of inference

In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...

 that, if B follows from A, and A follows from B, then A if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

B.

For example, from the statements "if I'm breathing, then I'm alive" and "if I'm alive, then I'm breathing", it can be inferred that "I'm breathing if and only if I'm alive".

Formally, biconditional introduction is the rule schema.