Contradiction
Encyclopedia
In classical logic
, a contradiction consists of a logical incompatibility between two or more proposition
s. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other. Illustrating a general tendency in applied logic, Aristotle’s
law of noncontradiction
states that “One cannot say of something that it is and that it is not in the same respect and at the same time.”
By extension, outside of classical logic
, one can speak of contradictions between actions when one presumes that their motives contradict each other.
Dialog of Euthydemus
demonstrates the need for the notion of contradiction. In the ensuing dialog Dionysodorus denies the existence of "contradiction", all the while that Socrates is contradicting him:
Indeed, Dionysodorus agrees that "there is no such thing as false opinion . . . there is no such thing as ignorance" and demands of Plato to "Refute me." Socrates responds "But how can I refute you, if, as you say, to tell a falsehood is impossible?".
In classical logic
, particularly in propositional and first-order logic
, a proposition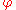
is a contradiction if and only if
. Since for contradictory 
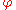it is true that 
for all 
(because 
), one may prove any proposition from a set of axioms which contains contradictions. This is called the "principle of explosion
" or "ex falso quodlibet" ("from falsity, whatever you like").
In a complete
logic, a formula is contradictory if and only if it is unsatisfiable.
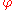it is true that 
, i. e. that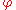 
is a tautology
, i. e. that it is always true, if and only if
, i. e. if the negation of 
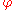is a contradiction. Therefore, a proof that 
also proves that 
is true. The use of this fact constitutes the technique of the proof by contradiction, which mathematicians use extensively. This applies only in a logic using the excluded middle 
as an axiom.
or some variant immediately after a contradiction symbol; this occurs in a proof by contradiction, to indicate that the original assumption was false and that the theorem must therefore be true.
requires (i) an axiomatic system
(ii) a demonstration that it is not the case that both the formula p and its negation ~p can derived in the system. But by whatever method one goes about it, all consistency proofs would seem to necessitate the primitive notion of contradiction; moreover, it seems as if this notion would simultaneously have to be "outside" the formal system in the definition of tautology
.
When Emil Post in his 1921 Introduction to a general theory of elementary propositions extended his proof of the consistency of the propositional calculus
(i.e. the logic) beyond that of Principia Mathematica
(PM) he observed that with respect to a generalized set of postulates (i.e. axioms) he would no longer be able to automatically invoke the notion of "contradiction" – such a notion might not be contained in the postulates:
Post's solution to the problem is described in the demonstration An Example of a Successful Absolute Proof of Consistency offered by Ernest Nagel
and James R. Newman
in their 1958 Gödel
's Proof. They too observe a problem with respect to the notion of "contradiction" with its usual "truth values" of "truth" and "falsity". They observe that:
Given some "primitive formulas" such as PM's primitives S1 V S2 [inclusive OR], ~S (negation) one is forced to define the axioms in terms of these primitive notions. In a thorough manner Post demonstrates in PM, and defines (as do Nagel and Newman, see below), that the property of tautologous – as yet to be defined – is "inherited": if one begins with a set of tautologous axioms (postulates) and a deduction system that contains substitution
and modus ponens
then a consistent system will yield only tautologous formulas.
So what will be the definition of tautologous?
Nagel and Newman create two mutually exclusive
and exhaustive classes K1 and K2 into which fall (the outcome of) the axioms when their variables e.g. S1 and S2 are assigned from these classes. This also applies to the primitive formulas. For example: "A formula having the form S1 V S2 is placed into class K2 if both S1 and S2 are in K2; otherwise it is placed in K1", and "A formula having the form ~S is placed in K2, if S is in K1; otherwise it is placed in K1".
Nagel and Newman can now define the notion of tautologous
: "a formula is a tautology if, and only if, it falls in the class K1 no matter in which of the two classes its elements are placed". Now the property of "being tautologous" is described without reference to a model or an interpretation.
Post observed that, if the system were inconsistent, a deduction in it (that is, the last formula in a sequence of formulas derived from the tautologies) could ultimately yield S itself. As as an assignment to variable S can come from either class K1 or K2, the deduction violates the inheritance characteristic of tautology, i.e. the derivation must yield an (evaluation of a formula) that will fall into class K1. From this, Post was able to derive the following definition of inconsistency without the use of the notion of contradiction:
In other words, the notion of "contradiction" can be dispensed when constructing a proof of consistency; what replaces it is the notion of "mutually exclusive and exhaustive" classes. More interestingly, an axiomatic system need not include the notion of "contradiction".
typically claim that as a necessary condition of the justification of a belief
, that belief must form a part of a logically non-contradictory (consistent) system
of beliefs. Some dialetheists
, including Graham Priest
, have argued that coherence may not require consistency.
For examples, arguably, Nietzsche’s statement that one should not obey others, or Moore's paradox
. Within the analytic tradition, these are seen as self-refuting statements and performative contradiction
s. Other traditions may read them more like zen
koans, in which the author purposes makes a contradiction using the traditional meaning, but then implies a new meaning of the word which does not contradict the statement.
, contradiction, as derived by Karl Marx
from Hegelianism
, usually refers to an opposition inherently existing within one realm, one unified force or object. This contradiction, as opposed to metaphysical thinking, is not an objectively impossible thing, because these contradicting forces exist in objective reality, not cancelling each other out, but actually defining each other's existence. According to Marxist theory, such a contradiction can be found, for example, in the fact that:
Hegelian and Marxist theory stipulates that the dialectic nature of history will lead to the sublation
, or synthesis
, of its contradictions. Marx therefore postulated that history would logically make capitalism
evolve into a socialist society
where the means of production
would equally serve the exploited and suffering class
of society, thus resolving the prior contradiction between (a) and (b).
Mao Zedong's philosophical essay
furthered Marx and Lenin's thesis and suggested that all existence is the result of contradiction.
can label actions and/or statements as contradicting each other when due (or perceived as due) to presupposition
s which are contradictory in the logical sense.
Proof by contradiction is used in mathematics
to construct proofs
.
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, a contradiction consists of a logical incompatibility between two or more proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other. Illustrating a general tendency in applied logic, Aristotle’s
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
law of noncontradiction
Law of noncontradiction
In classical logic, the law of non-contradiction is the second of the so-called three classic laws of thought. It states that contradictory statements cannot both at the same time be true, e.g...
states that “One cannot say of something that it is and that it is not in the same respect and at the same time.”
By extension, outside of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, one can speak of contradictions between actions when one presumes that their motives contradict each other.
History
By creation of a paradox Plato'sPlato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
Dialog of Euthydemus
Euthydemus
-People:*Euthydemus , a fleet commander for Athens during the Sicilian Expedition, 415 to 413 BC*Euthydemus, son of Cephalus, mentioned in Plato's Republic...
demonstrates the need for the notion of contradiction. In the ensuing dialog Dionysodorus denies the existence of "contradiction", all the while that Socrates is contradicting him:
- ". . . I in my astonishment said: What do you mean Dionysodorus? I have often heard, and have been amazed to hear, this thesis of yours, which is maintained and employed by the disciples of ProtagorasProtagorasProtagoras was a pre-Socratic Greek philosopher and is numbered as one of the sophists by Plato. In his dialogue Protagoras, Plato credits him with having invented the role of the professional sophist or teacher of virtue...
and others before them, and which to me appears to be quite wonderful, and suicidal as well as destructive, and I think that I am most likely to hear the truth about it from you. The dictum is that there is no such thing as a falsehood; a man must either say what is true or say nothing. Is not that your position?
Indeed, Dionysodorus agrees that "there is no such thing as false opinion . . . there is no such thing as ignorance" and demands of Plato to "Refute me." Socrates responds "But how can I refute you, if, as you say, to tell a falsehood is impossible?".
Contradiction in formal logic
- Note: The symbol
(falsum) represents an arbitrary contradiction, with the dual teeTee (symbol)A tee is a symbol used to represent:*Top element in lattice theory.*A logical constant denoting a tautology in logic.In Unicode the symbol is encoded .-See also:*⊢*Falsum, Up tack: *Table of mathematical symbols...
symbol
used to denote an arbitrary tautology. Contradiction is sometimes symbolized by "Opq", and tautology by "Vpq". The turnstile symbol, 
is often read as "yields" or "proves".
In classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, particularly in propositional and first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, a proposition
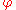is a contradiction if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
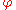. Since for contradictory it is true that for all (because ), one may prove any proposition from a set of axioms which contains contradictions. This is called the "principle of explosionPrinciple of explosion
The principle of explosion, or the principle of Pseudo-Scotus, is the law of classical logic and intuitionistic and similar systems of logic, according to which any statement can be proven from a contradiction...
" or "ex falso quodlibet" ("from falsity, whatever you like").
In a complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
logic, a formula is contradictory if and only if it is unsatisfiable.
Proof by contradiction
For a proposition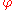 it is true that , i. e. that 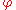is a tautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, i. e. that it is always true, if and only if
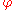, i. e. if the negation of is a contradiction. Therefore, a proof that also proves that is true. The use of this fact constitutes the technique of the proof by contradiction, which mathematicians use extensively. This applies only in a logic using the excluded middle as an axiom.Symbolic representation
In mathematics, the symbol used to represent a contradiction within a proof varies. http://www.ctan.org/tex-archive/info/symbols/comprehensive/symbols-a4.pdf Some symbols that may be used to represent a contradiction include ↯, Opq, ⇒⇐ , ⊥, ↮, and ※. It is not uncommon to see Q.E.D.Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
or some variant immediately after a contradiction symbol; this occurs in a proof by contradiction, to indicate that the original assumption was false and that the theorem must therefore be true.
The notion of contradiction in an axiomatic system and a proof of its consistency
A Consistency proofConsistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
requires (i) an axiomatic system
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
(ii) a demonstration that it is not the case that both the formula p and its negation ~p can derived in the system. But by whatever method one goes about it, all consistency proofs would seem to necessitate the primitive notion of contradiction; moreover, it seems as if this notion would simultaneously have to be "outside" the formal system in the definition of tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
.
When Emil Post in his 1921 Introduction to a general theory of elementary propositions extended his proof of the consistency of the propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
(i.e. the logic) beyond that of Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
(PM) he observed that with respect to a generalized set of postulates (i.e. axioms) he would no longer be able to automatically invoke the notion of "contradiction" – such a notion might not be contained in the postulates:
- "The prime requisite of a set of postulates is that it be consistent. Since the ordinary notion of consistency involves that of contradiction, which again involves negation, and since this function does not appear in general as a primitive in [the generalized set of postulates] a new definition must be given".
Post's solution to the problem is described in the demonstration An Example of a Successful Absolute Proof of Consistency offered by Ernest Nagel
Ernest Nagel
Ernest Nagel was a Czech-American philosopher of science. Along with Rudolf Carnap, Hans Reichenbach, and Carl Hempel, he is sometimes seen as one of the major figures of the logical positivist movement....
and James R. Newman
James R. Newman
James Roy Newman was an American mathematician and mathematical historian. He was also a lawyer, practicing in the state of New York from 1929 to 1941...
in their 1958 Gödel
Godel
Godel or similar can mean:*Kurt Gödel , an Austrian logician, mathematician and philosopher*Gödel...
's Proof. They too observe a problem with respect to the notion of "contradiction" with its usual "truth values" of "truth" and "falsity". They observe that:
- "The property of being a tautology has been defined in notions of truth and falsity. Yet these notions obviously involve a reference to something outside the formula calculus. Therefore, the procedure mentioned in the text in effect offers an interpretation of the calculus, by supplying a model for the system. This being so, the authors have not done what they promised, namely, 'to define a property of formulas in terms of purely structural features of the formulas themselves'. [Indeed] . . . proofs of consistency which are based on models, and which argue from the truth of axioms to their consistency, merely shift the problem."
Given some "primitive formulas" such as PM's primitives S1 V S2 [inclusive OR], ~S (negation) one is forced to define the axioms in terms of these primitive notions. In a thorough manner Post demonstrates in PM, and defines (as do Nagel and Newman, see below), that the property of tautologous – as yet to be defined – is "inherited": if one begins with a set of tautologous axioms (postulates) and a deduction system that contains substitution
Substitution
Substitution may refer to:- Sciences :* Substitution , a syntactic transformation on strings of symbols of a formal language* Substitution of variables* Substitution cipher, a method of encryption...
and modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
then a consistent system will yield only tautologous formulas.
So what will be the definition of tautologous?
Nagel and Newman create two mutually exclusive
Mutually exclusive
In layman's terms, two events are mutually exclusive if they cannot occur at the same time. An example is tossing a coin once, which can result in either heads or tails, but not both....
and exhaustive classes K1 and K2 into which fall (the outcome of) the axioms when their variables e.g. S1 and S2 are assigned from these classes. This also applies to the primitive formulas. For example: "A formula having the form S1 V S2 is placed into class K2 if both S1 and S2 are in K2; otherwise it is placed in K1", and "A formula having the form ~S is placed in K2, if S is in K1; otherwise it is placed in K1".
Nagel and Newman can now define the notion of tautologous
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
: "a formula is a tautology if, and only if, it falls in the class K1 no matter in which of the two classes its elements are placed". Now the property of "being tautologous" is described without reference to a model or an interpretation.
- For example, given a formula such as ~S1 V S2 and an assignment of K1 to S1 and K2 to S2 one can evaluate the formula and place its outcome in one or the other of the classes. The assignment of K1 to ~S1 places ~S1 in K2, and now we can see that our assignment causes the formula to fall into class K2. Thus by definition our formula is not a tautology.
Post observed that, if the system were inconsistent, a deduction in it (that is, the last formula in a sequence of formulas derived from the tautologies) could ultimately yield S itself. As as an assignment to variable S can come from either class K1 or K2, the deduction violates the inheritance characteristic of tautology, i.e. the derivation must yield an (evaluation of a formula) that will fall into class K1. From this, Post was able to derive the following definition of inconsistency without the use of the notion of contradiction:
- Definition. A system will be said to be inconsistent if it yields the assertion of the unmodified variable p [S in the Newman and Nagel examples].
In other words, the notion of "contradiction" can be dispensed when constructing a proof of consistency; what replaces it is the notion of "mutually exclusive and exhaustive" classes. More interestingly, an axiomatic system need not include the notion of "contradiction".
Contradictions and philosophy
Adherents of the epistemological theory of coherentismCoherentism
There are two distinct types of coherentism. One refers to the coherence theory of truth. The other refers to the coherence theory of justification. The coherentist theory of justification characterizes epistemic justification as a property of a belief only if that belief is a member of a coherent...
typically claim that as a necessary condition of the justification of a belief
Belief
Belief is the psychological state in which an individual holds a proposition or premise to be true.-Belief, knowledge and epistemology:The terms belief and knowledge are used differently in philosophy....
, that belief must form a part of a logically non-contradictory (consistent) system
System
System is a set of interacting or interdependent components forming an integrated whole....
of beliefs. Some dialetheists
Dialetheism
Dialetheism is the view that some statements can be both true and false simultaneously. More precisely, it is the belief that there can be a true statement whose negation is also true...
, including Graham Priest
Graham Priest
Graham Priest is Boyce Gibson Professor of Philosophy at the University of Melbourne and Distinguished Professor of Philosophy at the CUNY Graduate Center, as well as a regular visitor at St. Andrews University. Priest is a fellow in residence at Ormond College. He was educated at the University...
, have argued that coherence may not require consistency.
Pragmatic contradictions
A pragmatic contradiction occurs when the very statement of the argument contradicts the claims it purports. An inconsistency arises, in this case, because the act of utterance, rather than the content of what is said, undermines its conclusion.For examples, arguably, Nietzsche’s statement that one should not obey others, or Moore's paradox
Moore's paradox
Moore's paradox concerns the putative absurdity involved in asserting a first-person present-tense sentence such as 'It's raining but I don't believe that it is raining' or 'It's raining but I believe that it is not raining'. The first author to note this apparent absurdity was G.E. Moore...
. Within the analytic tradition, these are seen as self-refuting statements and performative contradiction
Performative contradiction
A performative contradiction arises when the propositional content of a statement contradicts the presuppositions of asserting it. An example of a performative contradiction is the statement "this statement can't be asserted" because the very act of asserting it presupposes it can be...
s. Other traditions may read them more like zen
Zen
Zen is a school of Mahāyāna Buddhism founded by the Buddhist monk Bodhidharma. The word Zen is from the Japanese pronunciation of the Chinese word Chán , which in turn is derived from the Sanskrit word dhyāna, which can be approximately translated as "meditation" or "meditative state."Zen...
koans, in which the author purposes makes a contradiction using the traditional meaning, but then implies a new meaning of the word which does not contradict the statement.
Dialectical materialism
In dialectical materialismDialectical materialism
Dialectical materialism is a strand of Marxism synthesizing Hegel's dialectics. The idea was originally invented by Moses Hess and it was later developed by Karl Marx and Friedrich Engels...
, contradiction, as derived by Karl Marx
Karl Marx
Karl Heinrich Marx was a German philosopher, economist, sociologist, historian, journalist, and revolutionary socialist. His ideas played a significant role in the development of social science and the socialist political movement...
from Hegelianism
Hegelianism
Hegelianism is a collective term for schools of thought following or referring to G. W. F. Hegel's philosophy which can be summed up by the dictum that "the rational alone is real", which means that all reality is capable of being expressed in rational categories...
, usually refers to an opposition inherently existing within one realm, one unified force or object. This contradiction, as opposed to metaphysical thinking, is not an objectively impossible thing, because these contradicting forces exist in objective reality, not cancelling each other out, but actually defining each other's existence. According to Marxist theory, such a contradiction can be found, for example, in the fact that:
- (a) enormous wealth and productive powers coexist alongside:
- (b) extreme poverty and misery;
- (c) the existence of (a) being contrary to the existence of (b).
Hegelian and Marxist theory stipulates that the dialectic nature of history will lead to the sublation
Aufheben
Aufheben or Aufhebung is a German word with several seemingly contradictory meanings, including "to lift up", "to abolish", or "to sublate"...
, or synthesis
Thesis, antithesis, synthesis
The triad thesis, antithesis, synthesis is often used to describe the thought of German philosopher Georg Wilhelm Friedrich Hegel. Hegel never used the term himself, and almost all of his biographers have been eager to discredit it....
, of its contradictions. Marx therefore postulated that history would logically make capitalism
Capitalism
Capitalism is an economic system that became dominant in the Western world following the demise of feudalism. There is no consensus on the precise definition nor on how the term should be used as a historical category...
evolve into a socialist society
Socialism
Socialism is an economic system characterized by social ownership of the means of production and cooperative management of the economy; or a political philosophy advocating such a system. "Social ownership" may refer to any one of, or a combination of, the following: cooperative enterprises,...
where the means of production
Means of production
Means of production refers to physical, non-human inputs used in production—the factories, machines, and tools used to produce wealth — along with both infrastructural capital and natural capital. This includes the classical factors of production minus financial capital and minus human capital...
would equally serve the exploited and suffering class
Proletariat
The proletariat is a term used to identify a lower social class, usually the working class; a member of such a class is proletarian...
of society, thus resolving the prior contradiction between (a) and (b).
Mao Zedong's philosophical essay
On Contradiction (Mao Zedong)
Mao Zedong's On Contradiction is considered his most important philosophical essay. Along with On Practice it forms the philosophical underpinnings of the political ideology that would later become Maoism. It was written in August 1937 while Mao was at his guerrilla base in Yenan. Mao suggests...
furthered Marx and Lenin's thesis and suggested that all existence is the result of contradiction.
Contradiction outside formal logic
Colloquial usageColloquialism
A colloquialism is a word or phrase that is common in everyday, unconstrained conversation rather than in formal speech, academic writing, or paralinguistics. Dictionaries often display colloquial words and phrases with the abbreviation colloq. as an identifier...
can label actions and/or statements as contradicting each other when due (or perceived as due) to presupposition
Presupposition
In the branch of linguistics known as pragmatics, a presupposition is an implicit assumption about the world or background belief relating to an utterance whose truth is taken for granted in discourse...
s which are contradictory in the logical sense.
Proof by contradiction is used in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
to construct proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
.
See also
- Dialectical materialismDialectical materialismDialectical materialism is a strand of Marxism synthesizing Hegel's dialectics. The idea was originally invented by Moses Hess and it was later developed by Karl Marx and Friedrich Engels...
- DoublethinkDoublethinkDoublethink, a word coined by George Orwell in the novel 1984, describes the act of simultaneously accepting two mutually contradictory beliefs as correct, often in distinct social contexts. It is related to, but distinct from, hypocrisy and neutrality. Its opposite is cognitive dissonance, where...
- IronyIronyIrony is a rhetorical device, literary technique, or situation in which there is a sharp incongruity or discordance that goes beyond the simple and evident intention of words or actions...
- OxymoronOxymoronAn oxymoron is a figure of speech that combines contradictory terms...
- Paraconsistent logicParaconsistent logicA paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
- ParadoxParadoxSimilar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
- Square of oppositionSquare of oppositionIn the system of Aristotelian logic, the square of opposition is a diagram representing the different ways in which each of the four propositions of the system are logically related to each of the others...