
Hypercomputation
Encyclopedia
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation
of non-Turing-computable function
s, following super-recursive algorithm
s (see also supertask
). The term "super-Turing computation" appeared in a 1995 Science
paper by Hava Siegelmann
. The term "hypercomputation" was introduced in 1999 by Jack Copeland
and Diane Proudfoot.
The terms are not quite synonymous: "super-Turing computation" usually implies that the proposed model is supposed to be physically realizable, while "hypercomputation" does not.
in his 1939 paper Systems of logic based on ordinals. This paper investigated mathematical systems in which an oracle
was available, which could compute a single arbitrary (non-recursive) function from naturals
to naturals. He used this device to prove that even in those more powerful systems, undecidability
is still present. Turing's oracle machines are strictly mathematical abstractions, and are not physically realizable.
states that any function that is algorithmically computable can be computed by a Turing machine. Hypercomputers compute functions that a Turing machine cannot, hence, not computable in the Church-Turing sense.
An example of a problem a Turing machine cannot solve is the halting problem
. A Turing machine cannot decide if an arbitrary program halts or runs forever. Some proposed hypercomputers can simulate the program for an infinite number of steps and tell the user whether or not the program halted.
or advice function
embedded into an otherwise classical machine. Others allow access to some higher level of the arithmetic hierarchy. For example, supertasking Turing machines, under the usual assumptions, would be able to compute any predicate in the truth-table degree containing or
or 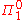 . Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree
. Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree
, which is known to be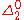 . Gold further showed that limiting partial recursion would allow the computation of precisely the
. Gold further showed that limiting partial recursion would allow the computation of precisely the  predicates.
predicates.
has collected a list of what he calls "super-recursive algorithms" (from Burgin 2005: 132):
In the same book, he presents also a list of "algorithmic schemes":
, in his writings on hypercomputation
refers to this subject as "a myth" and offers counter-arguments to the
physical realizability of hypercomputation. As for its theory, he argues against
the claims that this is a new field founded in 1990s. This point of view relies
on the history of computability theory (degrees of unsolvability, computability over
functions, real numbers and ordinals), as also mentioned above.
Andrew Hodges
wrote a critical commentary on Copeland and Proudfoot's article.
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
of non-Turing-computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s, following super-recursive algorithm
Super-recursive algorithm
In computability theory, super-recursive algorithms are a generalization of ordinary algorithms that are more powerful, that is, compute more than Turing machines. The term was introduced by Mark Burgin, whose book "Super-recursive algorithms" develops their theory and presents several mathematical...
s (see also supertask
Supertask
In philosophy, a supertask is a quantifiably infinite number of operations that occur sequentially within a finite interval of time. Supertasks are called "hypertasks" when the number of operations becomes innumerably infinite. The term supertask was coined by the philosopher James F...
). The term "super-Turing computation" appeared in a 1995 Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
paper by Hava Siegelmann
Hava Siegelmann
Hava Siegelmann is a computer scientist at the University of Massachusetts and director of the school's Biologically Inspired Neural and Dynamical Systems Lab. In the early 1990s she proposed a new computational model, the Artificial Recurrent Neural Network , and proved that it could perform...
. The term "hypercomputation" was introduced in 1999 by Jack Copeland
Jack Copeland
Brian Jack Copeland is Professor of Philosophy at the University of Canterbury, Christchurch, New Zealand.Copeland received a BPhil and DPhil from the University of Oxford in philosophy, where he undertook research on modal and non-classical logic.He is the Director of the Turing Archive for the...
and Diane Proudfoot.
The terms are not quite synonymous: "super-Turing computation" usually implies that the proposed model is supposed to be physically realizable, while "hypercomputation" does not.
History
A model more powerful than Turing machines was introduced by Alan TuringAlan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
in his 1939 paper Systems of logic based on ordinals. This paper investigated mathematical systems in which an oracle
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
was available, which could compute a single arbitrary (non-recursive) function from naturals
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
to naturals. He used this device to prove that even in those more powerful systems, undecidability
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
is still present. Turing's oracle machines are strictly mathematical abstractions, and are not physically realizable.
Hypercomputation and the Church–Turing thesis
The Church–Turing thesisChurch–Turing thesis
In computability theory, the Church–Turing thesis is a combined hypothesis about the nature of functions whose values are effectively calculable; in more modern terms, algorithmically computable...
states that any function that is algorithmically computable can be computed by a Turing machine. Hypercomputers compute functions that a Turing machine cannot, hence, not computable in the Church-Turing sense.
An example of a problem a Turing machine cannot solve is the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
. A Turing machine cannot decide if an arbitrary program halts or runs forever. Some proposed hypercomputers can simulate the program for an infinite number of steps and tell the user whether or not the program halted.
Hypercomputer proposals
- A Turing machine that can complete infinitely many steps. Simply being able to run for an unbounded number of steps does not suffice. One mathematical model is the Zeno machineZeno machineIn mathematics and computer science, Zeno machines are a hypothetical computational model related to Turing machines that allows a countably infinite number of algorithmic steps to be performed in finite time...
(inspired by Zeno's paradox). The Zeno machine performs its first computation step in (say) 1 minute, the second step in ½ minute, the third step in ¼ minute, etc. By summing 1+½+¼+... (a geometric series) we see that the machine performs infinitely many steps in a total of 2 minutes. However, some people claim that, following the reasoning from Zeno's paradox, Zeno machines are not just physically impossible, but logically impossible. Another example uses time dilationTime dilationIn the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
to allow a computer to spend an infinite amount of time performing a computation while a finite amount of time passes for an observer (it would require an infinite amount of energy to perform this calculation—see Malament-Hogarth spacetimeMalament-Hogarth spacetimeA Malament–Hogarth spacetime, named after David B. Malament and Mark Hogarth, is a relativistic spacetime that possesses the following property: there exists a worldline \lambda and an event p such that all events along \lambda are a finite interval in the past of p, but the proper time...
). - Turing's original oracle machines, defined in Turing 1939.
- In mid 1960s, E Mark Gold and Hilary PutnamHilary PutnamHilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
independently proposed models of inductive inferenceInductive inferenceAround 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
(the "limiting recursive functionals" and "trial-and-error predicates", respectively). These models enable some nonrecursive sets of numbers or languages (including all recursively enumerable sets of languages) to be "learned in the limit"; whereas, by definition, only recursive sets of numbers or languages could be identified by a Turing machine. While the machine will stabilize to the correct answer on any learnable set in some finite time, it can only identify it as correct if it is recursive; otherwise, the correctness is established only by running the machine forever and noting that it never revises its answer. Putnam identified this new interpretation as the class of "empirical" predicates, stating: "if we always 'posit' that the most recently generated answer is correct, we will make a finite number of mistakes, but we will eventually get the correct answer. (Note, however, that even if we have gotten to the correct answer (the end of the finite sequence) we are never sure that we have the correct answer.)" L. K. Schubert's 1974 paper "Iterated Limiting Recursion and the Program Minimization Problem" studied the effects of iterating the limiting procedure; this allows any arithmetic predicate to be computed. Schubert wrote, "Intuitively, iterated limiting identification might be regarded as higher-order inductive inference performed collectively by an ever-growing community of lower order inductive inference machines." - A real computer (a sort of idealized analog computerAnalog computerAn analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
) can perform hypercomputation if physics admits general realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables (not just computable realsComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
), and these are in some way "harnessable" for computation. This might require quite bizarre laws of physics (for example, a measurable physical constantPhysical constantA physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
with an oracular value, such as Chaitin's constantChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
), and would at minimum require the ability to measure a real-valued physical value to arbitrary precision despite thermal noise and quantumQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
effects. - A proposed technique known as fair nondeterminism or unbounded nondeterminismUnbounded nondeterminismIn computer science, unbounded nondeterminism or unbounded indeterminacy is a property of concurrency by which the amount of delay in servicing a request can become unbounded as a result of arbitration of contention for shared resources while still guaranteeing that the request will eventually be...
may allow the computation of noncomputable functions. There is dispute in the literature over whether this technique is coherent, and whether it actually allows noncomputable functions to be "computed". - It seems natural that the possibility of time travel (existence of closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s (CTCs)) makes hypercomputation possible by itself. However, this is not so since a CTC does not provide (by itself) the unbounded amount of storage that an infinite computation would require. Nevertheless, there are spacetimes in which the CTC region can be used for relativistic hypercomputation. Access to a CTC may allow the rapid solution to PSPACE-completePSPACE-completeIn complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
problems, a complexity class which while Turing-decidable is generally considered computationally intractable. - According to a 1992 paper, a computer operating in a Malament-Hogarth spacetimeMalament-Hogarth spacetimeA Malament–Hogarth spacetime, named after David B. Malament and Mark Hogarth, is a relativistic spacetime that possesses the following property: there exists a worldline \lambda and an event p such that all events along \lambda are a finite interval in the past of p, but the proper time...
or in orbit around a rotating black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
could theoretically perform non-Turing computations. - In 1994, Hava SiegelmannHava SiegelmannHava Siegelmann is a computer scientist at the University of Massachusetts and director of the school's Biologically Inspired Neural and Dynamical Systems Lab. In the early 1990s she proposed a new computational model, the Artificial Recurrent Neural Network , and proved that it could perform...
proved that her new (1991) computational model, the Artificial Recurrent Neural Network (ARNN), could perform hypercomputation (using infinite precision real weights for the synapses). It is based on evolving an artificial neural network through a discrete, infinite succession of states. - The infinite time Turing machine is a generalization of the Zeno machine, that can perform infinitely long computations whose steps are enumerated by potentially transfinite ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s. It models an otherwise-ordinary Turing machine for which non-halting computations are completed by entering a special state reserved for reaching a limit ordinal and to which the results of the preceding infinite computation are available. - Jan van LeeuwenJan van LeeuwenJan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
and Jiří Wiedermann wrote a 2000 paper suggesting that the Internet should be modeled as a nonuniform computing system equipped with an adviceAdvice (complexity)In computational complexity theory, an advice string is an extra input to a Turing machine which is allowed to depend on the length n of the input, but not on input itself...
function representing the ability of computers to be upgraded. - A symbol sequence is computable in the limit if there is a finite, possibly non-halting program on a universal Turing machineUniversal Turing machineIn computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π and of every other computable real, but still excludes all noncomputable reals. Traditional Turing machines cannot edit their previous outputs; generalized Turing machines, as defined by Jürgen SchmidhuberJürgen SchmidhuberJürgen Schmidhuber is a computer scientist and artist known for his work on machine learning, universal Artificial Intelligence , artificial neural networks, digital physics, and low-complexity art. His contributions also include generalizations of Kolmogorov complexity and the Speed Prior...
, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges, that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt GödelKurt GödelKurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
(1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
could be solved. Schmidhuber uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everythingTheory of everythingA theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
. Generalized Turing machines can solve the halting problem by evaluating a Specker sequenceSpecker sequenceIn computability theory, a Specker sequence is a computable, strictly increasing, bounded sequence of rational numbers whose supremum is not a computable real number. The first example of such a sequence was constructed by Ernst Specker in 1949....
. - A quantum mechanicalQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
system which somehow uses an infinite superposition of states to compute a non-computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
. This is not possible using the standard qubitQubitIn quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
-model quantum computerQuantum computerA quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
, because it is proven that a regular quantum computer is PSPACE-reducible (a quantum computer running in polynomial time can be simulated by a classical computer running in polynomial space). - In 1970, E.S. Santos defined a class of fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
-based "fuzzy algorithms" and "fuzzy Turing machines". Subsequently, L. Biacino and G. Gerla showed that such a definition would allow the computation of nonrecursive languages; they suggested an alternative set of definitions without this difficulty. Jiří Wiedermann analyzed the capabilities of Santos' original proposal in 2004. - Dmytro Taranovsky has proposed a finitisticFinitismIn the philosophy of mathematics, one of the varieties of finitism is an extreme form of constructivism, according to which a mathematical object does not exist unless it can be constructed from natural numbers in a finite number of steps...
model of traditionally non-finitistic branches of analysis, built around a Turing machine equipped with a rapidly increasing function as its oracle. By this and more complicated models he was able to give an interpretation of second-order arithmetic.
Analysis of capabilities
Many hypercomputation proposals amount to alternative ways to read an oracleOracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
or advice function
Advice (complexity)
In computational complexity theory, an advice string is an extra input to a Turing machine which is allowed to depend on the length n of the input, but not on input itself...
embedded into an otherwise classical machine. Others allow access to some higher level of the arithmetic hierarchy. For example, supertasking Turing machines, under the usual assumptions, would be able to compute any predicate in the truth-table degree containing
 or
or 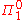 . Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree
. Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degreeTuring degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
, which is known to be
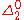 . Gold further showed that limiting partial recursion would allow the computation of precisely the
. Gold further showed that limiting partial recursion would allow the computation of precisely the  predicates.
predicates.| Model | Computable predicates | Notes | Refs |
|---|---|---|---|
| supertasking | tt( ) ) |
dependent on outside observer | |
| limiting/trial-and-error |  |
||
| iterated limiting (k times) |  |
||
| Blum-Shub-Smale machine Blum-Shub-Smale machine In computation theory, the Blum–Shub–Smale machine, or BSS machine, is a model of computation introduced by Lenore Blum, Michael Shub and Stephen Smale, intended to describe computations over the real numbers... |
incomparable with traditional computable real functions. | ||
| Malament-Hogarth spacetime | HYP | Dependent on spacetime structure | |
| Analog recurrent neural network | 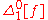 |
f is an advice function giving connection weights; size is bounded by runtime | |
| Infinite time Turing machine | 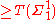 |
||
| Classical fuzzy Turing machine |  |
For any computable t-norm T-norm fuzzy logics T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction... |
|
| Increasing function oracle | 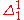 |
For the one-sequence model; 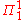 are r.e. are r.e. |
Taxonomy of "super-recursive" computation methodologies
BurginBurgin
-People:* Diana Lewis Burgin* Mona Burgin* Elise Burgin* Eric Burgin* Graham Burgin* James Burgin* Leslie Burgin, British politician* Melchior Bürgin* Rachel Burgin* Richard Burgin, Polish-American violinist...
has collected a list of what he calls "super-recursive algorithms" (from Burgin 2005: 132):
- limiting recursive functions and limiting partial recursive functions (E. M. Gold)
- trial and error predicates (Hilary PutnamHilary PutnamHilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
) - inductive inferenceInductive inferenceAround 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
machines (Carl Herbert SmithCarl Herbert SmithCarl Herbert Smith was a prominent American computer scientist. He was a pioneer in computational complexity and learning theory....
) - inductive Turing machines (one of Burgin's own models)
- limit Turing machines (another of Burgin's models)
- trial-and-error machines (Ja. Hintikka and A. Mutanen )
- general Turing machines (J. Schmidhuber)
- Internet machines (van Leeuwen, J.Jan van LeeuwenJan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
and Wiedermann, J.) - evolutionary computers, which use DNA to produce the value of a function (Darko Roglic)
- fuzzy computation (Jiří Wiedermann)
- evolutionary Turing machines (Eugene Eberbach)
In the same book, he presents also a list of "algorithmic schemes":
- Turing machines with arbitrary oracles (Alan Turing)
- Transrecursive operators (Borodyanskii and Burgin)
- machines that compute with real numbersReal computationIn computability theory, the theory of real computation deals with hypothetical computing machines using infinite-precision real numbers. They are given this name because they operate on the set of real numbers...
(L. Blum, F. Cucker, M. Shub, and S. Smale) - neural networks based on real numbers (Hava Siegelmann)
Criticism
Martin DavisMartin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, in his writings on hypercomputation
refers to this subject as "a myth" and offers counter-arguments to the
physical realizability of hypercomputation. As for its theory, he argues against
the claims that this is a new field founded in 1990s. This point of view relies
on the history of computability theory (degrees of unsolvability, computability over
functions, real numbers and ordinals), as also mentioned above.
Andrew Hodges
Andrew Hodges
Andrew Hodges is a mathematician, an author and a pioneer of the gay liberation movement of the 1970s.For the past decades , Hodges has focused his research activities on the twistor theory — the new approach to the problems of fundamental physics pioneered by the mathematician Roger...
wrote a critical commentary on Copeland and Proudfoot's article.
Further reading
- Hava SiegelmannHava SiegelmannHava Siegelmann is a computer scientist at the University of Massachusetts and director of the school's Biologically Inspired Neural and Dynamical Systems Lab. In the early 1990s she proposed a new computational model, the Artificial Recurrent Neural Network , and proved that it could perform...
and Eduardo Sontag, “Analog Computation via Neural Networks,” Theoretical Computer Science 131, 1994: 331-360. - Hava SiegelmannHava SiegelmannHava Siegelmann is a computer scientist at the University of Massachusetts and director of the school's Biologically Inspired Neural and Dynamical Systems Lab. In the early 1990s she proposed a new computational model, the Artificial Recurrent Neural Network , and proved that it could perform...
. Neural Networks and Analog Computation: Beyond the Turing Limit 1998 Boston: Birkhäuser (Book). - Mike Stannett, The case for hypercomputation, Applied Mathematics and Computation, Volume 178, Issue 1, 1 July 2006, Pages 8–24, Special Issue on Hypercomputation
- Keith Douglas. Super-Turing Computation: a Case Study Analysis (PDFPortable Document FormatPortable Document Format is an open standard for document exchange. This file format, created by Adobe Systems in 1993, is used for representing documents in a manner independent of application software, hardware, and operating systems....
), M.S. Thesis, Carnegie Mellon University, 2003. - L. Blum, F. Cucker, M. Shub, S. Smale, Complexity and Real Computation, Springer-Verlag 1997. General development of complexity theory for abstract machineAbstract machineAn abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...
s that compute on real numbersReal computationIn computability theory, the theory of real computation deals with hypothetical computing machines using infinite-precision real numbers. They are given this name because they operate on the set of real numbers...
instead of bits.
- [ftp://ftp.cs.cuhk.hk/pub/neuro/papers/jcss1.ps.Z On the computational power of neural nets]
- Toby Ord. Hypercomputation: Computing more than the Turing machine can compute: A survey article on various forms of hypercomputation.
- Apostolos Syropoulos (2008), Hypercomputation: Computing Beyond the Church-Turing Barrier (preview), Springer. ISBN 9780387308869
- Burgin, M. S. (1983) Inductive Turing Machines, Notices of the Academy of Sciences of the USSR, v. 270, No. 6, pp. 1289–1293
- Mark Burgin (2005), Super-recursive algorithms, Monographs in computer science, Springer. ISBN 0387955690
- Cockshott, P. and Michaelson, G. Are there new Models of Computation? Reply to Wegner and Eberbach, The computer Journal, 2007
- Copeland, J. (2002) Hypercomputation, Minds and machines, v. 12, pp. 461–502
- Martin Davis (2006), "The Church–Turing Thesis: Consensus and opposition". Proceedings, Computability in Europe 2006. Lecture notes in computer science, 3988 pp. 125–132
- Hagar, A. and Korolev, A., Quantum Hypercomputation—Hype or Computation?, (2007)
- Rogers, H. (1987) Theory of Recursive Functions and Effective Computability, MIT Press, Cambridge Massachusetts
- Volkmar Putz and Karl Svozil, Can a computer be "pushed" to perform faster-than-light?, (2010)
External links
- Hypercomputation Research Network
- Hypercomputation
- Toby Ord, Hypercomputation: computing more than the Turing machine
- Toby Ord, The many forms of hypercomputation
- Paolo Cotogno, Hypercomputation and the Physical Church-Turing thesis
- Gualtiero PiccininiGualtiero PiccininiGualtiero Piccinini is a philosopher working primarily on the nature of mind and computation as well as on how to integrate psychology and neuroscience. He is an associate professor in the Philosophy and Psychology Departments and the Center for Neurodynamics at the University of Missouri, St...
, Computation in Physical Systems

