Normal number
Encyclopedia
In mathematics
, a normal number is a real number
whose infinite sequence of digits
in every base
b is distributed uniformly in the sense that each of the b digit values has the same natural density
1/b, also all possible b2 pairs of digits are equally likely with density b−2, all b3 triplets of digits equally likely with density b−3, etc.
While a general proof can be given that almost all
numbers are normal (in the sense that the set of exceptions has Lebesgue measure
zero), this proof is not constructive
and only very few concrete numbers have been shown to be normal. For example, it is widely believed that the numbers √2
, π
, and e
are normal, but a proof remains elusive.
s that may be drawn from that alphabet. Let S,w ∈ Σ∞ be two such sequences, of which the latter is finite string drawn from the alphabet Σ. Let n be a positive integer. Define NS(w, n) to be the number of times the string w appears as a substring
in the first n digits of the sequence S. (For instance, if S = 01010101..., then NS(010, 8) = 3.) S is normal if, for all finite strings w ∈ Σ∞,
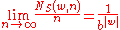
(where | w | denotes the length of the string w; see also limit
.)
In other words, S is normal if all strings of equal length occur with equal asymptotic
frequency. For example, in a normal binary sequence (a sequence over the alphabet {0,1}), 0 and 1 each occur with frequency 1⁄2; 00, 01, 10, and 11 each occur with frequency 1⁄4; 000, 001, 010, 011, 100, 101, 110, and 111 each occur with frequency 1⁄8, etc. Roughly speaking, the probability
of finding the string w in any given position in S is precisely that expected if the sequence had been produced at random
.
Suppose now that b is an integer
greater than 1 and x is a real number
. Consider the infinite digit sequence expansion Sx, b of x in the base b positional number system
(we ignore the decimal point). We say x is normal in base b if the sequence Sx, b is normal. The number x is called a normal number (or sometimes an absolutely normal number) if it is normal in base b for every integer b greater than 1.
A given infinite sequence is either normal or not normal, whereas a real number, having a different base-b expansion for each integer b ≥ 2, may be normal in one base but not in another (Cassels
1959 and Schmidt
1960). All normal numbers in base r are normal in base s if and only if log r / log s is a rational number (Schmidt 1960).
A disjunctive sequence
is a sequence in which every finite string appears. A normal sequence is disjunctive, but a disjunctive sequence need not be normal. A number that is disjunctive to every base is called absolutely disjunctive or is said to be a lexicon (Calude and Zamfirescu, 1999). A lexicon contains all writings, which have been or will be ever written, in any possible language. Every normal number is b-dense, but not necessarily vice versa. A set is called "residual" if it contains the intersection of a countable family of open dense sets. The set of absolutely disjunctive reals (lexicons) is a residual (Calude and Zamfirescu, 1999).
Another weaker property than normality is simple normality. A number is simply normal in base b if each individual digit appears with frequency 1/b. For a given base b, a number can be simply normal (but not normal or b-dense), b-dense (but not simply normal or normal), normal (and thus simply normal and b-dense), or none of these.
in 1909. Using the Borel-Cantelli lemma
, he proved the normal number theorem: almost all
real numbers are normal, in the sense that the set of non-normal numbers has Lebesgue measure
zero (Borel 1909). This theorem established the existence of normal numbers. In 1917, Waclaw Sierpinski showed that it is possible to specify a particular such number. Becker and Figueira proved in 2002 that there is a computable
normal number.
The set of non-normal numbers, though "small" in the sense of being a null set
, is "large" in the sense of being uncountable. For instance, there are uncountably many numbers whose decimal expansion does not contain the digit 5, and none of these are normal.
Champernowne's number
obtained by concatenating the decimal representations of the natural numbers in order, is normal in base 10, but it might not be normal in some other bases.
The Copeland–Erdős constant
obtained by concatenating the prime number
s in base 10, is normal in base 10, as proved by Copeland and Erdős (1946). More generally, the latter authors proved that the real number represented in base b by the concatenation
where f(n) is the nth prime expressed in base b, is normal in base b. Besicovitch
(1935) proved that the number represented by the same expression, with f(n) = n2,
obtained by concatenating the square number
s in base 10, is normal in base 10. Davenport & Erdős (1952) proved that the number represented by the same expression, with f being any polynomial whose values on the positive integers are positive integers, expressed in base 10, is normal in base 10.
Nakai & Shiokawa (1992) proved that if f(x) is any non-constant polynomial
with real coefficients such that f(x) > 0 for all x > 0, then the real number represented by the concatenation
where [f(n)] is the integer part of f(n) expressed in base b, is normal in base b. (This result includes as special cases all of the above-mentioned results of Champernowne, Besicovitch, and Davenport & Erdős.) The authors also show that the same result holds even more generally when f is any function of the form
where the α's and β's are real numbers with β > β1 > β2 > ... > βd ≥ 0, and f(x) > 0 for all x > 0.
Every Chaitin's constant
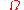is a normal number (Calude, 1994).
A computable
normal number was constructed in (Becher 2002). Although these constructions do not directly give the digits of the numbers constructed, the second shows that it is possible in principle to enumerate all the digits of a particular normal number.
No rational number
is normal to any base, since the digit sequences of rational numbers are eventually periodic
.
Bailey and Crandall show an explicit uncountably infinite class of b-normal numbers by perturbing Stoneham number
s.
It has been an elusive goal to prove the normality of numbers which were not explicitly constructed for the purpose. It is for instance unknown whether √2, π
, ln
(2) or e
is normal (but all of them are strongly conjectured to be normal, because of some empirical evidence). It is not even known whether all digits occur infinitely often in the decimal expansions of those constants. It has been conjectured that every irrational
algebraic number
is normal; while no counterexamples are known, there also exists no algebraic number that has been proven to be normal in any base.
Additional properties of normal numbers include:
is also normal. In other words, if one runs a finite-state machine on a normal sequence, where each of the finite-state machine's states are labeled either "output" or "no output", and the machine outputs the digit it reads next after entering an "output" state, but does not output the next digit after entering a "no output state", then the sequence it outputs will be normal (Agafonov 1968).
A deeper connection exists with finite-state gamblers (FSGs) and information lossless finite-state compressors (ILFSCs).
Schnorr and Stimm showed that no FSG can succeed on any normal sequence, and Bourke, Hitchcock and Vinodchandran showed the converse. Therefore:
Ziv and Lempel showed:
(they actually showed that the sequence's optimal compression ratio over all ILFSCs is exactly its entropy
rate, a quantitative measure of its deviation from normality, which is 1 exactly when the sequence is normal). Since the LZ compression algorithm compresses asymptotically as well as any ILFSC, this means that the LZ compression algorithm can compress any non-normal sequence. (Ziv Lempel 1978)
These characterizations of normal sequences can be interpreted to mean that "normal" = "finite-state random"; i.e., the normal sequences are precisely those that appear random to any finite-state machine. Compare this with the algorithmically random sequence
s, which are those infinite sequences that appear random to any algorithm (and in fact have similar gambling and compression characterizations with Turing machine
s replacing finite-state machines).
the sequence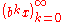
is equidistributed modulo 1, or equivalently, using Weyl's criterion
, if and only if
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a normal number is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
whose infinite sequence of digits
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
in every base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
b is distributed uniformly in the sense that each of the b digit values has the same natural density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
1/b, also all possible b2 pairs of digits are equally likely with density b−2, all b3 triplets of digits equally likely with density b−3, etc.
While a general proof can be given that almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
numbers are normal (in the sense that the set of exceptions has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero), this proof is not constructive
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
and only very few concrete numbers have been shown to be normal. For example, it is widely believed that the numbers √2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, and e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
are normal, but a proof remains elusive.
Definitions
Let Σ be a finite alphabet of b digits, and Σ∞ the set of all sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s that may be drawn from that alphabet. Let S,w ∈ Σ∞ be two such sequences, of which the latter is finite string drawn from the alphabet Σ. Let n be a positive integer. Define NS(w, n) to be the number of times the string w appears as a substring
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
in the first n digits of the sequence S. (For instance, if S = 01010101..., then NS(010, 8) = 3.) S is normal if, for all finite strings w ∈ Σ∞,
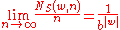
(where | w | denotes the length of the string w; see also limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
.)
In other words, S is normal if all strings of equal length occur with equal asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
frequency. For example, in a normal binary sequence (a sequence over the alphabet {0,1}), 0 and 1 each occur with frequency 1⁄2; 00, 01, 10, and 11 each occur with frequency 1⁄4; 000, 001, 010, 011, 100, 101, 110, and 111 each occur with frequency 1⁄8, etc. Roughly speaking, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of finding the string w in any given position in S is precisely that expected if the sequence had been produced at random
Random sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...
.
Suppose now that b is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than 1 and x is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Consider the infinite digit sequence expansion Sx, b of x in the base b positional number system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
(we ignore the decimal point). We say x is normal in base b if the sequence Sx, b is normal. The number x is called a normal number (or sometimes an absolutely normal number) if it is normal in base b for every integer b greater than 1.
A given infinite sequence is either normal or not normal, whereas a real number, having a different base-b expansion for each integer b ≥ 2, may be normal in one base but not in another (Cassels
J. W. S. Cassels
John William Scott Cassels , FRS is a leading English mathematician.-Biography:Educated at Neville's Cross Council School in Durham and George Heriot's School in Edinburgh, Cassels graduated from the University of Edinburgh with an MA in 1943.His academic career was interrupted in World War II...
1959 and Schmidt
Wolfgang M. Schmidt
Wolfgang M. Schmidt is a mathematician born in 1933. He studied mathematics at the University of Vienna, where he received his PhD, which was supervised by Edmund Hlawka, in 1955...
1960). All normal numbers in base r are normal in base s if and only if log r / log s is a rational number (Schmidt 1960).
A disjunctive sequence
Disjunctive sequence
A disjunctive sequence is an infinite sequence in which every finite string appears as a substring. For instance, the binary Champernowne sequence0\ 1\ 00\ 01\ 10\ 11\ 000\ 001 \ldots...
is a sequence in which every finite string appears. A normal sequence is disjunctive, but a disjunctive sequence need not be normal. A number that is disjunctive to every base is called absolutely disjunctive or is said to be a lexicon (Calude and Zamfirescu, 1999). A lexicon contains all writings, which have been or will be ever written, in any possible language. Every normal number is b-dense, but not necessarily vice versa. A set is called "residual" if it contains the intersection of a countable family of open dense sets. The set of absolutely disjunctive reals (lexicons) is a residual (Calude and Zamfirescu, 1999).
Another weaker property than normality is simple normality. A number is simply normal in base b if each individual digit appears with frequency 1/b. For a given base b, a number can be simply normal (but not normal or b-dense), b-dense (but not simply normal or normal), normal (and thus simply normal and b-dense), or none of these.
Properties and examples
The concept of a normal number was introduced by Émile BorelÉmile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
in 1909. Using the Borel-Cantelli lemma
Borel-Cantelli lemma
In probability theory, the Borel–Cantelli lemma is a theorem about sequences of events. In general, it is a result in measure theory. It is named after Émile Borel and Francesco Paolo Cantelli...
, he proved the normal number theorem: almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real numbers are normal, in the sense that the set of non-normal numbers has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero (Borel 1909). This theorem established the existence of normal numbers. In 1917, Waclaw Sierpinski showed that it is possible to specify a particular such number. Becker and Figueira proved in 2002 that there is a computable
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
normal number.
The set of non-normal numbers, though "small" in the sense of being a null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, is "large" in the sense of being uncountable. For instance, there are uncountably many numbers whose decimal expansion does not contain the digit 5, and none of these are normal.
Champernowne's number
Champernowne constant
In mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G...
- 0.1234567891011121314151617...,
obtained by concatenating the decimal representations of the natural numbers in order, is normal in base 10, but it might not be normal in some other bases.
The Copeland–Erdős constant
- 0.235711131719232931374143...,
obtained by concatenating the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s in base 10, is normal in base 10, as proved by Copeland and Erdős (1946). More generally, the latter authors proved that the real number represented in base b by the concatenation
- 0.f(1)f(2)f(3)...,
where f(n) is the nth prime expressed in base b, is normal in base b. Besicovitch
Abram Samoilovitch Besicovitch
Abram Samoilovitch Besicovitch was a Russian mathematician, who worked mainly in England. He was born in Berdyansk on the Sea of Azov to a Karaite family.-Life and career:...
(1935) proved that the number represented by the same expression, with f(n) = n2,
- 0.149162536496481100121144...,
obtained by concatenating the square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s in base 10, is normal in base 10. Davenport & Erdős (1952) proved that the number represented by the same expression, with f being any polynomial whose values on the positive integers are positive integers, expressed in base 10, is normal in base 10.
Nakai & Shiokawa (1992) proved that if f(x) is any non-constant polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with real coefficients such that f(x) > 0 for all x > 0, then the real number represented by the concatenation
- 0.[f(1)][f(2)][f(3)]...,
where [f(n)] is the integer part of f(n) expressed in base b, is normal in base b. (This result includes as special cases all of the above-mentioned results of Champernowne, Besicovitch, and Davenport & Erdős.) The authors also show that the same result holds even more generally when f is any function of the form
- f(x) = α·xβ + α1·xβ1 + ... + αd·xβd,
where the α's and β's are real numbers with β > β1 > β2 > ... > βd ≥ 0, and f(x) > 0 for all x > 0.
Every Chaitin's constant
Chaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
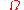is a normal number (Calude, 1994).A computable
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
normal number was constructed in (Becher 2002). Although these constructions do not directly give the digits of the numbers constructed, the second shows that it is possible in principle to enumerate all the digits of a particular normal number.
No rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is normal to any base, since the digit sequences of rational numbers are eventually periodic
Repeating decimal
In arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...
.
Bailey and Crandall show an explicit uncountably infinite class of b-normal numbers by perturbing Stoneham number
Stoneham number
In mathematics, the Stoneham numbers are a certain class of real numbers, named after mathematician Richard G. Stoneham . For coprime numbers b, c > 1, the Stoneham number αb,c is defined as...
s.
It has been an elusive goal to prove the normality of numbers which were not explicitly constructed for the purpose. It is for instance unknown whether √2, π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, ln
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(2) or e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
is normal (but all of them are strongly conjectured to be normal, because of some empirical evidence). It is not even known whether all digits occur infinitely often in the decimal expansions of those constants. It has been conjectured that every irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
is normal; while no counterexamples are known, there also exists no algebraic number that has been proven to be normal in any base.
Additional properties of normal numbers include:
- Every positive number x is the product of two normal numbers. For instance if y is chosen uniformly at randomUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
from the interval (0,1) then almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
y and x/y are both normal, and their product is x.
- If x is normal in base b and q ≠ 0 is a rational number, then
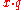is normal in base b. (Wall 1949)
- If
is dense (for every 
and for all sufficiently large n,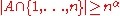 
) and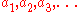 
are the base-b expansions of the elements of A, then the number 
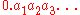, formed by concatenating the elements of A, is normal in base b (Copeland and Erdős 1946). From this it follows that Champernowne's number is normal in base 10 (since the set of all positive integers is obviously dense) and that the Copeland-Erdős constant is normal in base 10 (since the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
implies that the set of primes is dense).
- A sequence is normal if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
every block of equal length appears with equal frequency. (A block of length k is a substring of length k appearing at a position in the sequence that is a multiple of k: e.g. the first length-k block in S is S[1..k], the second length-k block is S[k+1..2k], etc.) This was implicit in the work of Ziv and Lempel (1978) and made explicit in the work of Bourke, Hitchcock, and Vinodchandran (2005).
- A number is normal in base b if and only if it is simply normal in base bk for every integer
. This follows from the previous block characterization of normality: Since the nth block of length k in its base b expansion corresponds to the nth digit in its base bk expansion, a number is simply normal in base bk if and only if blocks of length k appear in its base b expansion with equal frequency.
- A number is normal if and only if it is simply normal in every base. This follows from the previous characterization of base b normality.
- A number is b-normal if and only if there exists a set of positive integers
where the number is simply normal to bases bm for all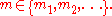 
No finite set suffices to show that the number is b-normal.
- The set of normal sequences is closed under finite variations: adding, removing, or changing a finite number of digits in any normal sequence leaves it normal.
Connection to finite-state machines
Agafonov showed an early connection between finite-state machines and normal sequences: every subsequence selected from a normal sequence by a regular languageRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
is also normal. In other words, if one runs a finite-state machine on a normal sequence, where each of the finite-state machine's states are labeled either "output" or "no output", and the machine outputs the digit it reads next after entering an "output" state, but does not output the next digit after entering a "no output state", then the sequence it outputs will be normal (Agafonov 1968).
A deeper connection exists with finite-state gamblers (FSGs) and information lossless finite-state compressors (ILFSCs).
- A finite-state gambler (a.k.a. finite-state martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
) is a finite-state machine over a finite alphabet
, each of whose states is labelled with percentages of money to bet on each digit in 
. For instance, for an FSG over the binary alphabet 
, the current state q bets some percentage 
of the gambler's money on the bit 0, and the remaining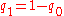 
fraction of the gambler's money on the bit 1. The money bet on the digit that comes next in the input (total money times percent bet) is multiplied by 
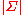, and the rest of the money is lost. After the bit is read, the FSG transitions to the next state according to the input it received. A FSG d succeeds on an infinite sequence S if, starting from $1, it makes unbounded money betting on the sequence; i.e., if
where
is the amount of money the gambler d has after reading the first n digits of S (see limit superior).
- A finite-state compressor is a finite-state machine with output strings labelling its state transitionsState transition tableIn automata theory and sequential logic, a state transition table is a table showing what state a finite semiautomaton or finite state machine will move to, based on the current state and other inputs...
, including possibly the empty string. (Since one digit is read from the input sequence for each state transition, it is necessary to be able to output the empty string in order to achieve any compression at all). An information lossless finite-state compressor is a finite-state compressor whose input can be uniquely recovered from its output and final state. In other words, for a finite-state compressor C with state set Q, C is information lossless if the function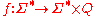
, mapping the input string of C to the output string and final state of C, is 1-1Injective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. Compression techniques such as Huffman codingHuffman codingIn computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
or Shannon-Fano coding can be implemented with ILFSCs. An ILFSC C compresses an infinite sequence S if
where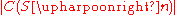
is the number of digits output by C after reading the first n digits of S. Note that the compression ratioData compression ratioData compression ratio, also known as compression power, is a computer-science term used to quantify the reduction in data-representation size produced by a data compression algorithm...
(the limit inferior above) can always be made to equal 1 by the 1-state ILFSC that simply copies its input to the output.
Schnorr and Stimm showed that no FSG can succeed on any normal sequence, and Bourke, Hitchcock and Vinodchandran showed the converse. Therefore:
- A sequence is normal if and only if there is no finite-state gambler that succeeds on it.
Ziv and Lempel showed:
- A sequence is normal if and only if it is incompressible by any information lossless finite-state compressor
(they actually showed that the sequence's optimal compression ratio over all ILFSCs is exactly its entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
rate, a quantitative measure of its deviation from normality, which is 1 exactly when the sequence is normal). Since the LZ compression algorithm compresses asymptotically as well as any ILFSC, this means that the LZ compression algorithm can compress any non-normal sequence. (Ziv Lempel 1978)
These characterizations of normal sequences can be interpreted to mean that "normal" = "finite-state random"; i.e., the normal sequences are precisely those that appear random to any finite-state machine. Compare this with the algorithmically random sequence
Algorithmically random sequence
Intuitively, an algorithmically random sequence is an infinite sequence ofbinary digits that appears random to any algorithm...
s, which are those infinite sequences that appear random to any algorithm (and in fact have similar gambling and compression characterizations with Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s replacing finite-state machines).
Connection to equidistributed sequences
A number x is normal in base b if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the sequence
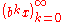is equidistributed modulo 1, or equivalently, using Weyl's criterionWeyl's criterion
In mathematics, in the theory of diophantine approximation, Weyl's criterion states that a sequence of real numbers is equidistributed mod 1 if and only if for all non-zero integers \ell we have:...
, if and only if