Algorithmically random sequence
Encyclopedia
Intuitively, an algorithmically random sequence (or random sequence) is an infinite sequence of
binary digits that appears random to any algorithm. The definition applies equally well to sequences on any finite set of characters
.
Random sequences are key objects of study in algorithmic information theory
.
As different types of algorithms are sometimes considered, ranging from algorithms with specific bounds on their running time to algorithms which may ask questions of an oracle, there are different notions of randomness. The most common of these is known as Martin-Löf randomness (or 1-randomness), but stronger and weaker forms of randomness also exist. The term "random" used to refer to a sequence without clarification is usually taken to mean "Martin-Löf random" (defined below).
Because infinite sequences of binary digits can be identified with real numbers in the unit interval, random binary sequences are often called random real numbers. Additionally, infinite binary sequences correspond to characteristic functions of sets of natural numbers; therefore those sequences might be seen as sets of natural numbers.
The class of all Martin-Löf random (binary) sequences is denoted by RAND or MLR.
in 1966. Earlier researchers such as Richard von Mises had attempted to formalize the notion of a test for randomness in order to define a random sequence as one that passed all tests for randomness; however, the precise notion of a randomness test was left vague. Martin-Löf's key insight was to use the theory of computation
to formally define the notion of a test for randomness. This contrasts with the idea of randomness in probability
; in that theory, no particular element of a sample space can be said to be random.
Martin-Löf randomness has since been shown to admit many equivalent characterizations — in terms of compression
, randomness tests, and gambling
— that bear little outward resemblance to the original definition, but each of which satisfy our intuitive notion of properties that random sequences ought to have: random sequences should be incompressible, they should pass statistical tests for randomness, and it should be difficult to make money betting on them. The existence of these multiple definitions of Martin-Löf randomness, and the stability of these definitions under different models of computation, give evidence that Martin-Löf randomness is a fundamental property of mathematics and not an accident of Martin-Löf's particular model. The thesis that the definition of Martin-Löf randomness "correctly" captures the intuitive notion of randomness has been called the Martin-Löf–Chaitin Thesis; it is somewhat similar to the Church–Turing thesis
.
and Claus-Peter Schnorr proved a characterization in terms of Kolmogorov complexity
: a sequence is random if there is a uniform bound on the compressibility of its initial segments. Schnorr gave a third equivalent definition in terms of martingales
(a type of betting strategy). Li and Vitanyi's book An Introduction to Kolmogorov Complexity and Its Applications is the standard introduction to these ideas.
The null cover characterization conveys the intuition that a random real number should not have any property that is “uncommon”. Each measure 0 set can be thought of as an uncommon property. It is not possible for a sequence to lie in no measure 0 sets, because each one-point set has measure 0. Martin-Löf's idea was to limit the definition to measure 0 sets that are effectively describable; the definition of an effective null cover determines a countable collection of effectively describable measure 0 sets and defines a sequence to be random if it does not lie in any of these particular measure 0 sets. Since the union of a countable collection of measure 0 sets has measure 0, this definition immediately leads to the theorem that there is a measure 1 set of random sequences. Note that if we identify the Cantor space of binary sequences with the interval [0,1] of real numbers, the measure on Cantor space agrees with Lebesgue measure
.
The martingale characterization conveys the intuition that no effective procedure should be able to make money betting against a random sequence. A martingale d is a betting strategy. d reads a finite string w and bets money on the next bit. It bets some fraction of its money that the next bit will be 0, and then remainder of its money that the next bit will be 1. d doubles the money it placed on the bit that actually occurred, and it loses the rest. d(w) is the amount of money it has after seeing the string w. Since the bet placed after seeing the string w can be calculated from the values d(w), d(w0), and d(w1), calculating the amount of money it has is equivalent to calculating the bet. The martingale characterization says that no betting strategy implementable by any computer (even in the weak sense of constructive strategies, which are not necessarily computable) can make money betting on a random sequence.
. For a fixed oracle A, a sequence B which is not only random but in fact satisfies the equivalent definitions for computability relative to A (e.g., no martingale which is constructive relative to the oracle A succeeds on B) is said to be random relative to A. Two sequences, while themselves random, may contain very similar information, and therefore neither will be random relative to the other. Any time there is a Turing reduction
from one sequence to another, the second sequence cannot be random relative to the first, just as computable sequences are themselves nonrandom; in particular, this means that Chaitin's Ω
is not random relative to the halting problem
.
An important result relating to relative randomness is van Lambalgen
's theorem, which states that if C is the sequence composed from A and B by interleaving the first bit of A, the first bit of B, the second bit of A, the second bit of B, and so on, then C is algorithmically random if and only if A is algorithmically random, and B is algorithmically random relative to A. A closely related consequence is that if A and B are both random themselves, then A is random relative to B if and only if B is random relative to A.
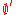, and the nth jump oracle, 
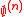, as these oracles are able to answer specific questions which naturally arise. A sequence which is random relative to the oracle 
is called n-random; a sequence is 1-random, therefore, if and only if it is Martin-Löf random. A sequence which is n-random for every n is called arithmetically random. The n-random sequences sometimes arise when considering more complicated properties. For example, there are only countably many 
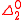sets, so one might think that these should be non-random. However, the halting probability Ω
is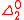
and 1-random; it is only after 2-randomness is reached that it is impossible for a random set to be 
.
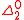binary digits that appears random to any algorithm. The definition applies equally well to sequences on any finite set of characters
Character (computing)
In computer and machine-based telecommunications terminology, a character is a unit of information that roughly corresponds to a grapheme, grapheme-like unit, or symbol, such as in an alphabet or syllabary in the written form of a natural language....
.
Random sequences are key objects of study in algorithmic information theory
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
.
As different types of algorithms are sometimes considered, ranging from algorithms with specific bounds on their running time to algorithms which may ask questions of an oracle, there are different notions of randomness. The most common of these is known as Martin-Löf randomness (or 1-randomness), but stronger and weaker forms of randomness also exist. The term "random" used to refer to a sequence without clarification is usually taken to mean "Martin-Löf random" (defined below).
Because infinite sequences of binary digits can be identified with real numbers in the unit interval, random binary sequences are often called random real numbers. Additionally, infinite binary sequences correspond to characteristic functions of sets of natural numbers; therefore those sequences might be seen as sets of natural numbers.
The class of all Martin-Löf random (binary) sequences is denoted by RAND or MLR.
History
The first suitable definition of a random sequence was given by Per Martin-LöfPer Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
in 1966. Earlier researchers such as Richard von Mises had attempted to formalize the notion of a test for randomness in order to define a random sequence as one that passed all tests for randomness; however, the precise notion of a randomness test was left vague. Martin-Löf's key insight was to use the theory of computation
Theory of computation
In theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
to formally define the notion of a test for randomness. This contrasts with the idea of randomness in probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
; in that theory, no particular element of a sample space can be said to be random.
Martin-Löf randomness has since been shown to admit many equivalent characterizations — in terms of compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, randomness tests, and gambling
Gambling
Gambling is the wagering of money or something of material value on an event with an uncertain outcome with the primary intent of winning additional money and/or material goods...
— that bear little outward resemblance to the original definition, but each of which satisfy our intuitive notion of properties that random sequences ought to have: random sequences should be incompressible, they should pass statistical tests for randomness, and it should be difficult to make money betting on them. The existence of these multiple definitions of Martin-Löf randomness, and the stability of these definitions under different models of computation, give evidence that Martin-Löf randomness is a fundamental property of mathematics and not an accident of Martin-Löf's particular model. The thesis that the definition of Martin-Löf randomness "correctly" captures the intuitive notion of randomness has been called the Martin-Löf–Chaitin Thesis; it is somewhat similar to the Church–Turing thesis
Church–Turing thesis
In computability theory, the Church–Turing thesis is a combined hypothesis about the nature of functions whose values are effectively calculable; in more modern terms, algorithmically computable...
.
Three equivalent definitions
Martin-Löf's original definition of a random sequence was in terms of constructive null covers; he defined a sequence to be random if it is not contained in any such cover. Leonid LevinLeonid Levin
-External links:* at Boston University....
and Claus-Peter Schnorr proved a characterization in terms of Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
: a sequence is random if there is a uniform bound on the compressibility of its initial segments. Schnorr gave a third equivalent definition in terms of martingales
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
(a type of betting strategy). Li and Vitanyi's book An Introduction to Kolmogorov Complexity and Its Applications is the standard introduction to these ideas.
- Kolmogorov complexity (Schnorr 1973, Levin 1973): Kolmogorov complexityKolmogorov complexityIn algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
can be thought of as a lower bound on the algorithmic compressibility of a finite sequence (of characters or binary digits). It assigns to each such sequence w a natural number K(w) that, intuitively, measures the minimum length of a computer program (written in some fixed programming language) that takes no input and will output w when run. Given a natural number c and a sequence w, we say that w is c-incompressible if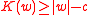
.
- An infinite sequence S is Martin-Löf random if and only if there is a constant c such that all of Ss finite prefixes are c-incompressible.
- Constructive null covers (Martin-Löf 1966): This is Martin-Löf's original definition. For a finite binary string w we let Cw denote the cylinder generated by w. This is the set of all infinite sequences beginning with w, which is a basic open set in Cantor spaceCantor spaceIn mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
. The product measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
μ(Cw) of the cylinder generated by w is defined to be 2-|w|. Every open subset of Cantor space is the union of a countable sequence of disjoint basic open sets, and the measure of an open set is the sum of the measures of any such sequence. An effective open set is an open set that is the union of the sequence of basic open sets determined by a recursively enumerable sequence of binary strings. A constructive null cover or effective measure 0 set is a recursively enumerable sequence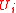
of effective open sets such that 
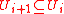and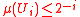 
for each natural number i. Every effective null cover determines a 
G-delta setIn the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
set of measure 0, namely the intersection of the sets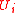
.
- A sequence is defined to be Martin-Löf random if it is not contained in any
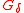set determined by a constructive null cover.
- Constructive martingales (Schnorr 1971): A martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
is a function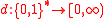
such that, for all finite strings w, 
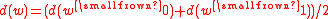, where 
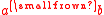is the concatenationConcatenationIn computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
of the strings a and b. This is called the "fairness condition"; a martingale is viewed as a betting strategy, and the above condition requires that the better plays against fair odds. A martingale d is said to succeed on a sequence S if
where 
is the first n bits of S. A martingale d is constructive (also known as weakly computable, lower semi-computable, subcomputable) if there exists a computable function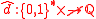 
such that, for all finite binary strings w
-
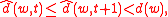for all positive integers t, -
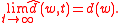
- A sequence is Martin-Löf random if and only if no constructive martingale succeeds on it.
Interpretations of the definitions
The Kolmogorov complexity characterization conveys the intuition that a random sequence is incompressible: no prefix can be produced by a program much shorter than the prefix.The null cover characterization conveys the intuition that a random real number should not have any property that is “uncommon”. Each measure 0 set can be thought of as an uncommon property. It is not possible for a sequence to lie in no measure 0 sets, because each one-point set has measure 0. Martin-Löf's idea was to limit the definition to measure 0 sets that are effectively describable; the definition of an effective null cover determines a countable collection of effectively describable measure 0 sets and defines a sequence to be random if it does not lie in any of these particular measure 0 sets. Since the union of a countable collection of measure 0 sets has measure 0, this definition immediately leads to the theorem that there is a measure 1 set of random sequences. Note that if we identify the Cantor space of binary sequences with the interval [0,1] of real numbers, the measure on Cantor space agrees with Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
The martingale characterization conveys the intuition that no effective procedure should be able to make money betting against a random sequence. A martingale d is a betting strategy. d reads a finite string w and bets money on the next bit. It bets some fraction of its money that the next bit will be 0, and then remainder of its money that the next bit will be 1. d doubles the money it placed on the bit that actually occurred, and it loses the rest. d(w) is the amount of money it has after seeing the string w. Since the bet placed after seeing the string w can be calculated from the values d(w), d(w0), and d(w1), calculating the amount of money it has is equivalent to calculating the bet. The martingale characterization says that no betting strategy implementable by any computer (even in the weak sense of constructive strategies, which are not necessarily computable) can make money betting on a random sequence.
Properties and examples of Martin-Löf random sequences
- Chaitin's halting probability ΩChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
is an example of a random sequence.
- RANDc (the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of RAND) is a measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
0 subset of the set of all infinite sequences. This is implied by the fact that each constructive null cover covers a measure 0 set, there are only countably many constructive null covers, and a countable union of measure 0 sets has measure 0. This implies that RAND is a measure 1 subset of the set of all infinite sequences.
- Every random sequence is normalNormal numberIn mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
.
- There is a constructive null cover of RANDc. This means that all effective tests for randomness (that is, constructive null covers) are, in a sense, subsumed by this universal test for randomness, since any sequence that passes this single test for randomness will pass all tests for randomness. (Martin-Löf 1966)
- There is a universal constructive martingale d. This martingale is universal in the sense that, given any constructive martingale d, if d succeeds on a sequence, then d succeeds on that sequence as well. Thus, d succeeds on every sequence in RANDc (but, since d is constructive, it succeeds on no sequence in RAND). (Schnorr 1971)
- The class RAND is a
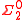subset of Cantor space, where 
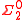refers to the second level of the arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
. This is because a sequence S is in RAND if and only if there is some open set in the universal effective null cover that does not contain S; this property can be seen to be definable by a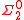
formula.
- There is a random sequence which is
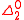, that is, computable relative to an oracle for the Halting problem. (Schnorr 1971) Chaitin's ΩChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
is an example of such a sequence.
- No random sequence is decidableDecidableThe word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
, computably enumerable, or co-computably-enumerable. Since these correspond to the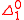
, 
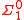, and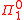 
levels of the arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
, this means that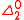
is the lowest level in the arithmetical hierarchy where random sequences can be found.
- Every sequence is Turing reducible to some random sequence. (Kučera 1985/1989, Gács 1986). Thus there are random sequences of arbitrarily high Turing degreeTuring degreeIn computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
.
Relative randomness
As each of the equivalent definitions of a Martin-Löf random sequence is based on what is computable by some Turing machine, one can naturally ask what is computable by a Turing oracle machineOracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
. For a fixed oracle A, a sequence B which is not only random but in fact satisfies the equivalent definitions for computability relative to A (e.g., no martingale which is constructive relative to the oracle A succeeds on B) is said to be random relative to A. Two sequences, while themselves random, may contain very similar information, and therefore neither will be random relative to the other. Any time there is a Turing reduction
Turing reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
from one sequence to another, the second sequence cannot be random relative to the first, just as computable sequences are themselves nonrandom; in particular, this means that Chaitin's Ω
Chaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
is not random relative to the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
.
An important result relating to relative randomness is van Lambalgen
Michiel van Lambalgen
Michiel van Lambalgen is a professor of Logic and Cognitive Science at the Institute for Logic, Language and Computation and the Department of Philosophy, University of Amsterdam in the Netherlands....
's theorem, which states that if C is the sequence composed from A and B by interleaving the first bit of A, the first bit of B, the second bit of A, the second bit of B, and so on, then C is algorithmically random if and only if A is algorithmically random, and B is algorithmically random relative to A. A closely related consequence is that if A and B are both random themselves, then A is random relative to B if and only if B is random relative to A.
Stronger than Martin-Löf randomness
Relative randomness gives us the first notion which is stronger than Martin-Löf randomness, which is randomness relative to some fixed oracle A. For any oracle, this is at least as strong, and for most oracles, it is strictly stronger, since there will be Martin-Löf random sequences which are not random relative to the oracle A. Important oracles often considered are the halting problem,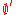, and the nth jump oracle, 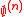, as these oracles are able to answer specific questions which naturally arise. A sequence which is random relative to the oracle is called n-random; a sequence is 1-random, therefore, if and only if it is Martin-Löf random. A sequence which is n-random for every n is called arithmetically random. The n-random sequences sometimes arise when considering more complicated properties. For example, there are only countably many 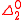sets, so one might think that these should be non-random. However, the halting probability ΩChaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
is
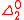and 1-random; it is only after 2-randomness is reached that it is impossible for a random set to be .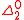