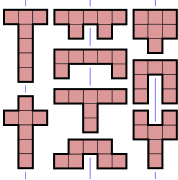
A heptomino is a polyomino

Polyomino

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....

 of order 7, that is, a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 in the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

 made of 7 equal-sized square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

s connected edge-to-edge. The name of this type of figure is formed with the prefix hept(a)-. When rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

s and reflection

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

s are not considered to be distinct shapes, there are 108

108 (number)

108 is the natural number following 107 and preceding 109.- In mathematics :One hundred [and] eight is an abundant number and a semiperfect number...

 different free heptominoes. When reflections are considered distinct, there are 196

196 (number)

196 is the natural number following 195 and preceding 197.-In mathematics:* 196 is an even number* 196 is an abundant number, as 203 is greater than 196* 196 is a composite number...

 one-sided heptominoes. When rotations are also considered distinct, there are 760 fixed heptominoes.

Symmetry

The figure shows all possible free heptominoes, coloured according to their symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

s:

• 84 heptominoes (coloured grey) have no symmetry
  Symmetry
  Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
  
  . Their symmetry group consists only of the identity mapping
  Identity function
  In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
  
  .

• 9 heptominoes (coloured red) have an axis of reflection symmetry
  Reflection symmetry
  Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
  
   aligned with the gridlines. Their symmetry group has two elements, the identity and the reflection in a line parallel to the sides of the squares.

• 7 heptominoes (coloured green) have an axis of reflection symmetry at 45° to the gridlines. Their symmetry group has two elements, the identity and a diagonal reflection.

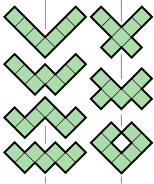
• 4 heptominoes (coloured blue) have point symmetry, also known as rotational symmetry
  Rotational symmetry
  Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
  
   of order 2. Their symmetry group has two elements, the identity and the 180° rotation.

• 3 heptominoes (coloured purple) have two axes of reflection symmetry, both aligned with the gridlines. Their symmetry group has four elements, the identity, two reflections and the 180° rotation. It is the dihedral group
  Dihedral group
  In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
  
   of order 2, also known as the Klein four-group
  Klein four-group
  In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
  
  .

• 1 heptomino (coloured orange) has two axes of reflection symmetry, both aligned with the diagonals. Its symmetry group also has four elements. Its symmetry group is also the dihedral group of order 2 with four elements.

If reflections of a heptomino are considered distinct, as they are with one-sided heptominoes, then the first and fourth categories above would each double in size, resulting in an extra 88 heptominoes for a total of 196. If rotations are also considered distinct, then the heptominoes from the first category count eightfold, the ones from the next three categories count fourfold, and the ones from the last two categories count twice. This results in 84 × 8 + (9+7+4) × 4 + (3+1) × 2 = 760 fixed heptominoes.

Packing and tiling

Although a complete set of 108 heptominoes has a total of 756 squares, it is not possible to pack

Packing problem

Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...

 them into a rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

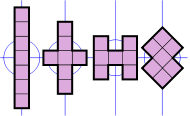
. The proof of this is trivial, since there is one heptomino which has a hole. It is also impossible to pack them into a 757-square rectangle with a one-square hole because 757 is a prime number.

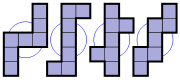
All but four heptominoes are capable of tiling the plane; the one with a hole is one such example.